Cursus / training:
Methode voor Causale Analyse
Voorspellende kracht
van
Steekproef kenmerken
naar
Individu
Geïllustreerd met enkele grafieken
.C.P. van der Velde
1.0: 06 Mar 2018 13:42.
Hieronder staan enkele grafieken die de praktische merites in perspectief plaatsen van het statistische begrip ' significantie'.
Dit in het licht van het eigenlijke doel van statistische toetsen: het beoordelen of een hypothese over een causale relatie redelijkerwijs kan worden opgenomen in een theorie. Voor dat laatste is nodig te bewijzen dat de causale hypothese voldoende voorspellende kracht heeft. Een minimaal criterium, of randvoorwaarde, is hierbij dat de stelling op zijn minst beter dan toeval, better than random, oftewel meer dan 50 procent correct voorspelt in de empirie.
Merkwaardig genoeg zien we op dit punt in veel wetenschappelijk onderzoek, met name in de sociale wetenschappen, een immens probleem: wijd verbreide misvattingen - en veelvuldig misbruik - van significantie. Kort gezegd, een statistisch significante uitkomst wordt veelal opgevat als bewijs voor de aanwezigheid van een 'beduidende' causale relatie, terwijl het enkel nog maar wijst op een 'beduidende' afwijking van louter toeval. Als bewijs of aanwijzing voor voorspellende kracht is het hoegenaamd irrelevant.
De enige gewettigde interpretatie van van een bepaalde statistische maat is precies omgekeerd: als er geen sprake is van voldoende statistische significantie kunnen we niet in redelijkheid concluderen dat sprake is van enige statistische (d.i. rekenkundige) verklarende of voorspellende waarde op basis van de gebruikte meetgegevens, dus nog minder van een werkelijke causale relatie in het betreffende referentieel domein.
(En dan nog zijn hierbij twee voorbehoudens op zijn plaats: (a) significantie kan alleen worden vastgesteld op basis van een tevoren aangenomen waarde (alpha) van de maximaal toegelaten toevalskans, die in wezen arbitrair is en geen al te stellige conclusies toelaat; (b) dat een conclusie vooralsnog niet kan worden afgeleid betekent zeker niet dat die conclusie daarmee weerlegd is).
De verhoudingen tussen diverse statistische maten van voorspellend vermogen zijn uitgewerkt in een aantal gedetailleerde cijfertabellen. Zie bijv. een samenvattende versie:
' Predictive power of sample correlation for deduction to N=1 samples - Matrix (9) Values of first significance, optimized'.
Hieronder zijn een aantal van die tabelgegevens in een grafiek gezet, in drie delen. Deze grafiek geeft al in één oogopslag helder inzicht in het gigantische probleem.
Deelgrafieken 1 t/m 3 tonen op de X-as het spectrum van de verkregen (eerste) steekproef correlatie.
(N.b., correlatie is niet meer dan de mate van symmetrische variatie tussen twee cijferreeksen. Het bewijst nog niets over een causaal verband. Integendeel, het omgekeerde geldt: een causale relatie impliceert oftewel vereist dat er voldoende correlatie tussen de waarden van oorzaak en gevolg bestaat. Met andere woorden: als we geen noemenswaardige correlatie kunnen aantonen, kunnen we met redelijke zekerheid aannemen dat er geen sprake is van een causale relatie).
Hierbij is een redelijk gebruikelijke sample size genomen: N = 100. Bij andere steekproefgroottes veranderen de verhoudingen niet wezenlijk.
Op de Y-assen van de deelgrafieken staan afgeleide statistische uitkomsten, respectievelijk:
(1) Geschatte gemiddelden van de gehele populatie;
(2) Voorspelde gemiddelden van een (nieuwe) steekproef;
en (3) Voorspelde eigenschappen bij individuele toepassingen ('N=1' voorspellingen).
(2) Voorspelde gemiddelden van een (nieuwe) steekproef;
en (3) Voorspelde eigenschappen bij individuele toepassingen ('N=1' voorspellingen).
De algemeen gangbare praktijk - in de sociale wetenschappen, maar ook media, opiniepeilers, enz. - is dat de statistische significantie uitkomst (ad 1a) nogal extreem foutief wordt gebruikt:
- in theorievorming toegepast alsof het (2b) betreft.
- in praktijktoepassingen toegepast alsof het (3b) betreft.
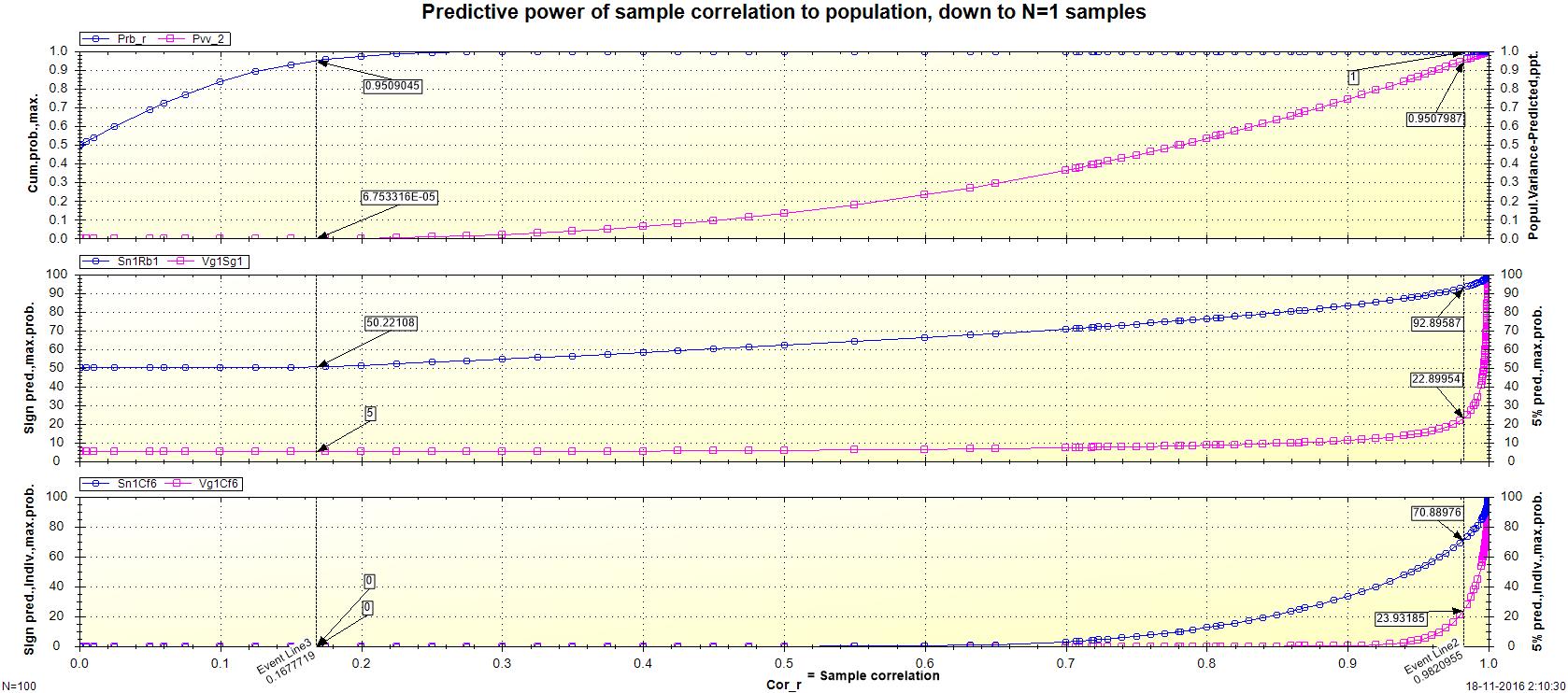
Grafiek: Voorspellende kracht van steekproef correlatie voor N=1 toepassingen
.(bij
N
=100, alpha =0.05, epsilon =0.05).Deelgrafiek 1: Geschatte populatie waarden.
1a.
Kanswaarde p voor non-random samenhang.
Deze kans bereikt een drempelwaarde van 95 % voor 'significantie' (bij alpha van 5 %), al bij een steekproef correlatie van tenminste 0.165, (zie in de grafiek 'Event Line 3').
Zo'n correlatie is uiteraard nogal minuscuul en wordt in het algemeen redelijk gemakkelijk gehaald in sociaal-wetenschappelijk onderzoek.
1b.
Proportie verklaarde populatie variantie.
Bij een p waarde van 95 % bedraagt de verklaarde populatie variantie nog vrijwel nul.
Voor better-than-random voorspelling moet deze proportie echter minstens 50 % zijn. Dat vraagt om een steekproef correlatie van minstens ca. 0.78.
Deze waarde bereikt een drempelwaarde van 95 % pas bij een steekproef correlatie van 0.98 (zie in de grafiek 'Event Line 2').
Y-as lijn, links /boven:
Kanswaarde p voor non-random samenhang.
Deze kans bereikt een drempelwaarde van 95 % voor 'significantie' (bij alpha van 5 %), al bij een steekproef correlatie van tenminste 0.165, (zie in de grafiek 'Event Line 3').
Zo'n correlatie is uiteraard nogal minuscuul en wordt in het algemeen redelijk gemakkelijk gehaald in sociaal-wetenschappelijk onderzoek.
1b.
Y-as lijn, rechts /middenonder:
Proportie verklaarde populatie variantie.
Bij een p waarde van 95 % bedraagt de verklaarde populatie variantie nog vrijwel nul.
Voor better-than-random voorspelling moet deze proportie echter minstens 50 % zijn. Dat vraagt om een steekproef correlatie van minstens ca. 0.78.
Deze waarde bereikt een drempelwaarde van 95 % pas bij een steekproef correlatie van 0.98 (zie in de grafiek 'Event Line 2').
Deelgrafiek 2: Verwachte waarden van een (nieuwe) steekproef, gemiddelden over individuen.
2a.
Kanswaarde voor betrouwbaarheid van gemiddelde 'succes' voorspelling (d.i. binnen de onderste of bovenste 50 %). Dit is de kans dat een score op de éne variabele - de 'oorzaak' - gemiddeld de ligging van een andere variabele - het 'effect' - ten opzichte van het populatiegemiddelde (d.i. standaardwaarde z=0.0) correct voorspelt.
De baseline van deze kans ligt uiteraard op 50 %, oftewel puur toeval.
(N.b. 50 % kans is compleet random, c.q. fifty-fifty, c.q. 'slag in de lucht'. Alles daaronder wijst op ongeldigheid van de onderzochte causale hypothese).
Bij een p waarde van 95 % bedraagt deze kans nog steeds vrijwel 50 %.
Bij een steekproef correlatie van 0.80 - die in de sociale wetenschappen meestal behoorlijk fors wordt gevonden - bedraagt deze kans 76.1 % : d.w.z. slechts ca. 3/4 better-then-random treffers in een nieuwe steekproef.
Ze bereikt een drempelwaarde van 95 % pas bij een steekproef correlatie van 0.99.
Dit komt dus ongeveer overeen met het complement van de benodigde correlatie voor significantie.
In het overgrote deel van sociaal-wetenschappelijk onderzoek wordt dit duidelijk niet gehaald. Wat we heel vaak zien is dat de gemiddelde verschillen (d.i. de statistische varianties) tussen individuen binnen de onderzochte groepen aanmerkelijk groter zijn dan de die tussen de groepen.
2b.
Kanswaarde voor betrouwbaarheid van gemiddelde voorspelling van elk half deciel (d.i. binnen elke 5 %, oftewel elk willekeurig 1/20 deel van de meetschaal).
De baseline van deze kans ligt uiteraard op 5 %.
Deze kans bereikt een drempelwaarde van 95 % pas bij een steekproef correlatie van 0.999.
Y-as lijn, links /boven:
Kanswaarde voor betrouwbaarheid van gemiddelde 'succes' voorspelling (d.i. binnen de onderste of bovenste 50 %). Dit is de kans dat een score op de éne variabele - de 'oorzaak' - gemiddeld de ligging van een andere variabele - het 'effect' - ten opzichte van het populatiegemiddelde (d.i. standaardwaarde z=0.0) correct voorspelt.
De baseline van deze kans ligt uiteraard op 50 %, oftewel puur toeval.
(N.b. 50 % kans is compleet random, c.q. fifty-fifty, c.q. 'slag in de lucht'. Alles daaronder wijst op ongeldigheid van de onderzochte causale hypothese).
Bij een p waarde van 95 % bedraagt deze kans nog steeds vrijwel 50 %.
Bij een steekproef correlatie van 0.80 - die in de sociale wetenschappen meestal behoorlijk fors wordt gevonden - bedraagt deze kans 76.1 % : d.w.z. slechts ca. 3/4 better-then-random treffers in een nieuwe steekproef.
Ze bereikt een drempelwaarde van 95 % pas bij een steekproef correlatie van 0.99.
Dit komt dus ongeveer overeen met het complement van de benodigde correlatie voor significantie.
In het overgrote deel van sociaal-wetenschappelijk onderzoek wordt dit duidelijk niet gehaald. Wat we heel vaak zien is dat de gemiddelde verschillen (d.i. de statistische varianties) tussen individuen binnen de onderzochte groepen aanmerkelijk groter zijn dan de die tussen de groepen.
2b.
Y-as lijn, rechts /middenonder:
Kanswaarde voor betrouwbaarheid van gemiddelde voorspelling van elk half deciel (d.i. binnen elke 5 %, oftewel elk willekeurig 1/20 deel van de meetschaal).
De baseline van deze kans ligt uiteraard op 5 %.
Deze kans bereikt een drempelwaarde van 95 % pas bij een steekproef correlatie van 0.999.
Deelgrafiek 3: Verwachte waarden (nieuwe) steekproef, specifiek voor individuen.
3a.
Kanswaarde voor minstens 95 % betrouwbaarheid van 'succes' voorspelling (d.i. binnen de onderste of bovenste 50 %) - voor een willekeurig individu. Dit is de kans dat een score op de éne variabele - de 'oorzaak' - per individu de ligging van een andere variabele - het 'effect' - ten opzichte van het populatiegemiddelde (d.i. standaardwaarde z=0.0) met minstens 95 % betrouwbaarheid correct voorspelt.
Deze kans begint pas enigszins van nul af te wijken bij een steekproefcorrelatie van ca. 0.63.
Bij een steekproefcorrelatie van 0.80 bedraagt deze kans nog steeds maar 12.5 % : dus één better-then-random treffer op acht individuen.
Ze ontstijgt de toevalskans pas bij een steekproefcorrelatie van ca. 0.98.
Deze kans bereikt een drempelwaarde van 95 % pas bij een steekproef correlatie van 0.9995.
Dit betekent dat er in geen van de onderzochte groepen ook maar één uitzondering c.q. tegenvoorbeeld is, waarvan de scores beter passen bij een andere groep.
Sterker nog, het betekent dat elke individu vrijwel naadloos overeenkomstig het gemiddelde groepsverschil van zijn/haar groep scoort.
(de standaardfout is vrijwel nul).
In de praktijk van sociaal wetenschappelijk onderzoek zal dit normaliter uiteraard onhaalbaar zijn, afgezien van grove fouten of trucs.
3b.
Kanswaarde voor minstens 95 % betrouwbaarheid van voorspelling van elk half deciel (d.i. binnen elke 5 %, oftewel elk willekeurig 1/20 deel van de meetschaal) - voor een willekeurig individu.
Deze kans begint pas enigszins van nul af te wijken bij een steekproefcorrelatie van ca. 0.90.
Ze ontstijgt de toevalskans pas bij een steekproefcorrelatie van ca. 0.995.
Deze kans bereikt een drempelwaarde van 95 % pas bij een steekproef correlatie van 0.99995.
Y-as lijn, links /boven:
Kanswaarde voor minstens 95 % betrouwbaarheid van 'succes' voorspelling (d.i. binnen de onderste of bovenste 50 %) - voor een willekeurig individu. Dit is de kans dat een score op de éne variabele - de 'oorzaak' - per individu de ligging van een andere variabele - het 'effect' - ten opzichte van het populatiegemiddelde (d.i. standaardwaarde z=0.0) met minstens 95 % betrouwbaarheid correct voorspelt.
Deze kans begint pas enigszins van nul af te wijken bij een steekproefcorrelatie van ca. 0.63.
Bij een steekproefcorrelatie van 0.80 bedraagt deze kans nog steeds maar 12.5 % : dus één better-then-random treffer op acht individuen.
Ze ontstijgt de toevalskans pas bij een steekproefcorrelatie van ca. 0.98.
Deze kans bereikt een drempelwaarde van 95 % pas bij een steekproef correlatie van 0.9995.
Dit betekent dat er in geen van de onderzochte groepen ook maar één uitzondering c.q. tegenvoorbeeld is, waarvan de scores beter passen bij een andere groep.
Sterker nog, het betekent dat elke individu vrijwel naadloos overeenkomstig het gemiddelde groepsverschil van zijn/haar groep scoort.
(de standaardfout is vrijwel nul).
In de praktijk van sociaal wetenschappelijk onderzoek zal dit normaliter uiteraard onhaalbaar zijn, afgezien van grove fouten of trucs.
3b.
Y-as lijn, rechts /middenonder:
Kanswaarde voor minstens 95 % betrouwbaarheid van voorspelling van elk half deciel (d.i. binnen elke 5 %, oftewel elk willekeurig 1/20 deel van de meetschaal) - voor een willekeurig individu.
Deze kans begint pas enigszins van nul af te wijken bij een steekproefcorrelatie van ca. 0.90.
Ze ontstijgt de toevalskans pas bij een steekproefcorrelatie van ca. 0.995.
Deze kans bereikt een drempelwaarde van 95 % pas bij een steekproef correlatie van 0.99995.
Conclusies
Het nut van het statistische begrip significantie als criterium om de validiteit van causale hypothesen te testen, in de zin van voldoende afwijking van toeval, blijkt zeer beperkt. Ze kan niet op een redelijke manier dienen om de validiteit van causale relaties in positieve zin te bevestigen.
De meest zinvolle toepassingen liggen op twee punten:
(1)
Wanneer een causale hypothese in statistische zin zelfs niet significant scoort, mag dat als voldoende bewijs dienen dat die hypothese niet aannemelijk is.
(2)
In de fase van exploratie kan significantie dienen als 'filter', om de causale hypothesen te selecteren die in aanmerking komen voor verder onderzoek - mits uiteraard aannemelijk is dat in de 'scherpte' van het onderzoek - in theoretische context, experimenteel ontwerp, steekproef trekking, uitvoeringspraktijk, meting, berekening, enz. - nog aanmerkelijke verbeteringen mogelijk zijn.
Ten behoeve van weerlegging:
Wanneer een causale hypothese in statistische zin zelfs niet significant scoort, mag dat als voldoende bewijs dienen dat die hypothese niet aannemelijk is.
(2)
Ten behoeve van bewijsvoering:
In de fase van exploratie kan significantie dienen als 'filter', om de causale hypothesen te selecteren die in aanmerking komen voor verder onderzoek - mits uiteraard aannemelijk is dat in de 'scherpte' van het onderzoek - in theoretische context, experimenteel ontwerp, steekproef trekking, uitvoeringspraktijk, meting, berekening, enz. - nog aanmerkelijke verbeteringen mogelijk zijn.
Zie ook ..
C.P. van der Velde © 2016, 2018.