Course / training:
Method for Causal Analysis
Predictive power
of
Sample Patterns
to
Individuals
Exemplified with some plots
.
C.P. van der Velde
1.0: 06 Mar 2018 13:42.
Below some graphs are depicted that may put practical merits into perspective of the statistical concept of ' significance'.
This in light of the actual purpose of statistical testing, which is to assess whether a hypothesis about a causal relation can reasonably be included in a theory. For the latter it is necessary to prove that the causal hypothesis has sufficient predictive power. A minimal criterion, or precondition, is that the theorem at least correctly predicts better than random, that is more then 50 percent, in the empirical world.
Curiously, on this point, we see an immense problem in many instances of scientific research, particularly in social sciences: widespread misconceptions - and frequent abuse - of significance. In short, a statistically significant outcome is often interpreted as evidence for the presence of a 'significant' causal relation, while it only points to a 'significant' deviation from mere coincidence in purely linear covariance of two or more sets of numbers.
As proof or indication of predictive power it is rather irrelevant.
The only legitimate interpretation of statistical significance of a given statistical measure is exactly the opposite: if there is no sufficient statistical significance we can not reasonably assume any meaningful statistical (i.e., computational) explanatory or predictive value based on the measurement data used, still less a real causal relationship in the relevant referential domain.
(And even then, two caveats are in order here: (a) significance can only be determined on the basis of a predefined value (alpha) of the maximum probability of chance accepted, which is essentially arbitrary and does not allow for rigorous conclusions; (b) the fact that a conclusion cannot be derived for the time being does not at all mean that the conclusion is thereby refuted).
The ratios between various statistical measures of predictive power have been elaborated in a number of detailed number tables. See eg for a summary overview:
' Predictive power of sample correlation for deduction to N=1 samples - Matrix (9) Values of first significance, optimized'.
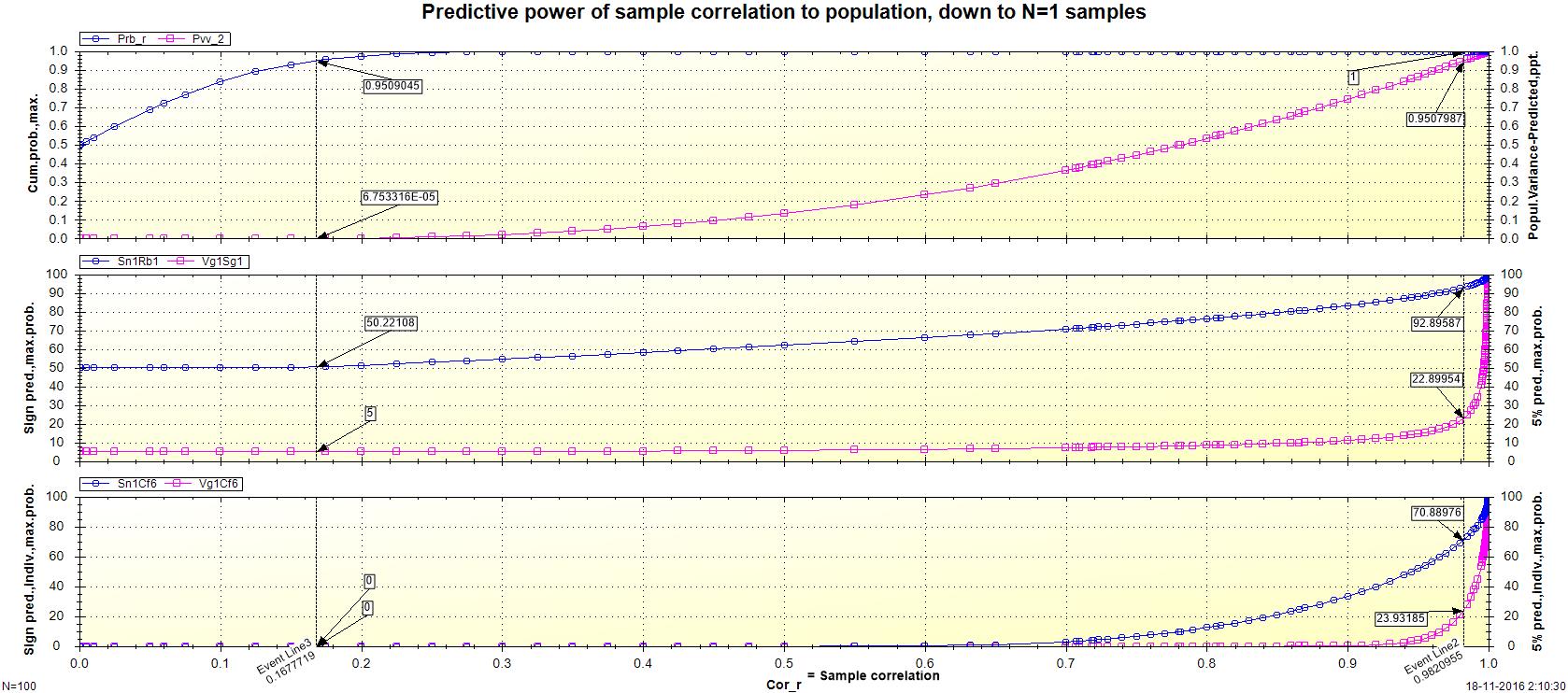
Below some of those table data are put on a graph, in three parts. This graph provides clear insight into the huge problem at a single glance.
Subgraphs 1 to 3 show on the X-axis the spectrum of the obtained (first) sample correlation.
(N.b., correlation is no more than the degree of symmetric variation between two or more sets of numbers; it does not prove anything about a causal relationship. On the contrary, the converse applies: a causal relationship implies or requires that there is sufficient correlation between the values of cause and effect. In other words: if we can't demonstrate a correlation of any notable size, we can reasonably assume that there is no causal relationship).
For the purpose of illumination, a reasonably customary sample size has been taken: N = 100. With other sample sizes, the ratios do not change in essence.
On the Y-axes of the subgraphs statistical results are represented, respectively:
(1) Estimated averages of the entire population;
(2) Predicted averages of a (new) sample;
and (3) Predicted properties in individual applications (ie. 'N=1' predictions).
(2) Predicted averages of a (new) sample;
and (3) Predicted properties in individual applications (ie. 'N=1' predictions).
The general practice - in the social sciences, but also media, opinion pollers, etc. - is that the outcome concerning statistical significance (ad 1a) is used rather extremely incorrectly:
- applied in theories as if it were (2b).
- applied in practical applications as if it were (3b).
Graph: Predictive power of sample correlation for N = 1 applications.
.(at
N
=100, alpha =0.05, epsilon =0.05).Sub-graph 1: Estimated population values.
1a.
Probability value p for non-random non-random coherence.
This probability reaches a threshold value of 95 % for 'significance' (at alpha of 5 %), even with a sample correlation of at least 0.165 (see in the graph 'Event Line 3').
Such correlation is quite tiny of course, and is in general rather easily met.
1b.
Proportion explained population variance.
At a p value of 95 %, the explaned population variance is still virtually zero.
For better-than-random prediction, however, this proportion must be at least 50 %. This requires a sample correlation of at least 0.78.
This value reaches a threshold value of 95 % only at a sample correlation of 0.98 (see in the graph 'Event Line 2').
Y-axis line, left / top:
Probability value p for non-random non-random coherence.
This probability reaches a threshold value of 95 % for 'significance' (at alpha of 5 %), even with a sample correlation of at least 0.165 (see in the graph 'Event Line 3').
Such correlation is quite tiny of course, and is in general rather easily met.
1b.
Y-axis line, right / center bottom:
Proportion explained population variance.
At a p value of 95 %, the explaned population variance is still virtually zero.
For better-than-random prediction, however, this proportion must be at least 50 %. This requires a sample correlation of at least 0.78.
This value reaches a threshold value of 95 % only at a sample correlation of 0.98 (see in the graph 'Event Line 2').
Sub-graph 2: Expected values in a (new) sample, averages about individuals.
2a.
Probability of reliability of 'sign' prediction (ie. within lower or upper 50 %) on average.
This is the probability that a score on the one variable - the 'cause' - predicts the location of another variable - the 'effect' - correctly on average relative to the population mean (i.e., default valuez = 0.0).
The baseline of this probability is of course at 50 %, or pure coincidence.
(N.b. A 50 % chance is completely random, or fifty-fifty, or 'shot in the dark'. Everything below this points to invalidity of the causal hypothesis under investigation).
At a p value of 95 %, this probability is still roughly 50 %.
In case of a sample correlation of 0.80 - which is usually considered quite high the social sciences - this probability is 76.1 %: i.e. only about 3/4 better-then-random hits in a new sample.
This probability reaches a minimum threshold of 95 % only at a sample correlation of 0.99.
We see that this roughly amounts to the complement of the correlation required for significance.
Clearly, in the vast majority of social science research this is not achieved. What we very often see is that the average differences (i.e. the statistical variances) between individuals within the groups examined are considerably larger then the differences between the groups.
2b.
Probability for reliability of average prediction of each half decile (i.e., within every 5 %, or any 1/20 part of the measuring scale).
The baseline of this probability is of course 5 %.
This probability reaches a threshold value of 95 % only at a sample correlation of 0.999.
This means that there is not one exception, or counter-example, in the groups examined that would better better fit in another group. Moreover, it means that every individuals scores nearly seamlessly corresponds to the average group difference of his/her group (the standard error is virtually zero).
In the practice of social scientific research this of course will not be feasible in most cases, apart from gross errors or tricks.
Y-axis line, left / top:
Probability of reliability of 'sign' prediction (ie. within lower or upper 50 %) on average.
This is the probability that a score on the one variable - the 'cause' - predicts the location of another variable - the 'effect' - correctly on average relative to the population mean (i.e., default value
The baseline of this probability is of course at 50 %, or pure coincidence.
(N.b. A 50 % chance is completely random, or fifty-fifty, or 'shot in the dark'. Everything below this points to invalidity of the causal hypothesis under investigation).
At a p value of 95 %, this probability is still roughly 50 %.
In case of a sample correlation of 0.80 - which is usually considered quite high the social sciences - this probability is 76.1 %: i.e. only about 3/4 better-then-random hits in a new sample.
This probability reaches a minimum threshold of 95 % only at a sample correlation of 0.99.
We see that this roughly amounts to the complement of the correlation required for significance.
Clearly, in the vast majority of social science research this is not achieved. What we very often see is that the average differences (i.e. the statistical variances) between individuals within the groups examined are considerably larger then the differences between the groups.
2b.
Y-axis line, right / center bottom:
Probability for reliability of average prediction of each half decile (i.e., within every 5 %, or any 1/20 part of the measuring scale).
The baseline of this probability is of course 5 %.
This probability reaches a threshold value of 95 % only at a sample correlation of 0.999.
This means that there is not one exception, or counter-example, in the groups examined that would better better fit in another group. Moreover, it means that every individuals scores nearly seamlessly corresponds to the average group difference of his/her group (the standard error is virtually zero).
In the practice of social scientific research this of course will not be feasible in most cases, apart from gross errors or tricks.
Sub-graph 3: Expected values in a (new) sample, specifically for individuals.
3a.
Probability of at least 95 % reliability of 'sign' prediction (ie. within lower or upper 50 %) - for any individual. This is the probability that a score on the one variable - the 'cause' - predicts the location of another variable - the 'effect' - correctly per individual relative to the population mean (i.e., default valuez = 0.0), with at least 95 % reliability.
This probability only starts to deviate slightly from zero at a sample correlation from approx. 0.63.
With a sample correlation of 0.80, this probability is still only 12.5 %: thus just one better-then-random hit on every eight individuals.
It becomes better then random only at a sample correlation from approx. 0.98.
This probability reaches a threshold value of 95 % only at a sample correlation of 0.9995.
3b.
Probability value for at least 95 % reliability of prediction of each half decile (i.e., within every 5 %, or any 1/20 part of the measuring scale) - for any individual.
This probability only starts to deviate slightly from zero in a sample correlation from approx. 0.90.
It becomes better then random only at a sample correlation from approx. 0.995.
This probability reaches a threshold value of 95 % only at a sample correlation of 0.99995.
Y-axis line, left / top:
Probability of at least 95 % reliability of 'sign' prediction (ie. within lower or upper 50 %) - for any individual. This is the probability that a score on the one variable - the 'cause' - predicts the location of another variable - the 'effect' - correctly per individual relative to the population mean (i.e., default value
This probability only starts to deviate slightly from zero at a sample correlation from approx. 0.63.
With a sample correlation of 0.80, this probability is still only 12.5 %: thus just one better-then-random hit on every eight individuals.
It becomes better then random only at a sample correlation from approx. 0.98.
This probability reaches a threshold value of 95 % only at a sample correlation of 0.9995.
3b.
Y axis line, right / center bottom:
Probability value for at least 95 % reliability of prediction of each half decile (i.e., within every 5 %, or any 1/20 part of the measuring scale) - for any individual.
This probability only starts to deviate slightly from zero in a sample correlation from approx. 0.90.
It becomes better then random only at a sample correlation from approx. 0.995.
This probability reaches a threshold value of 95 % only at a sample correlation of 0.99995.
Conclusions
The usefulness of the statistical concept of significance as a criterion to test the validity of causal hypotheses, in the sense of sufficient deviation from pure chance, appears to be very limited. She can not in a reasonable way serve to confirm the validity of causal hypotheses in a positive sense.
The most meaningful applications lie on two points:
(1)
When a causal hypothesis in statistical sense not even pears to be significant, that may serve sufficient evidence that that hypothesis is not plausible anyway.
(2)
In the phase of exploration significance may well serve as a 'filter', in order to select the causal hypotheses that qualify for further research - provided of course it is plausible that in the 'sharpness' of the research - on points of theoretical context, experimental design, sample draw, performance, measurement, calculation, etc. - significant improvements are still possible.
For falsification:
When a causal hypothesis in statistical sense not even pears to be significant, that may serve sufficient evidence that that hypothesis is not plausible anyway.
(2)
For verification:
In the phase of exploration significance may well serve as a 'filter', in order to select the causal hypotheses that qualify for further research - provided of course it is plausible that in the 'sharpness' of the research - on points of theoretical context, experimental design, sample draw, performance, measurement, calculation, etc. - significant improvements are still possible.
Zie ook ..
C.P. van der Velde © 2016, 2018.