Introductie_Predikatenlogica_PDL_Deel IIb_H

Cursus / training:

Methode Formele Logica

^©

II. Basiswetten in de predicatenlogica.

4. Semantiek voor Predikatenlogica.

Definities van waarheids- en geldigheidswaarden.
Axioma's, tautologieën, altijd geldige theorema's.

4.1. Interpretatie.

4.1.1. Predikatenlogica en de opbouw van kennis.

Predikatenlogica is een noodzakelijke grondslag voor de opbouw van zinvolle kennis.
Daarbij gaat het primair - dus niet uitsluitend - om de wijze waarop het 'veld' van waarnemingen, het domein, wordt overzien en geconceptualiseerd. Daarna kunnen we gaan zoeken naar mogelijke regelmatigheden, relaties, wetten en werkingsprincipes in het betreffende domein, bijvoorbeeld causale verbanden in de fysische empirie.

4.1.2. Relatie tussen syntax en betekenis van formules in de predikatenlogica.

(1)

Inhoudsvrije taal.

In de logica, of anders gezegd: elk adequaat logisch systeem, gaat het louter om structuur, oftewel 'abstracte vorm': aspecten van onderscheid, ordening, verhouding, samenhang, verwijzing en (on)afhankelijkheid.
Hoe dan ook is de taal van de logica op zichzelf altijd inherent inhoudsvrij, oftewel ongeïnterpreteerd: zonder enige aanname c.q. vooronderstelling over een bepaald gebied in de werkelijkheid. Ook het 'onderzoeksveld' (het referentiële domein) beschouwen we in eerste instantie zonder enige vooronderstelling, enkel als een verzameling van losse uitgangsgegevens. Dat wil zeggen, de objecten in een domein hebben zelf binnen het systeem verder géén eigenschappen: het zijn volkomen 'anonieme' en onderling verwisselbare individuen, zoals {x, y, .. } en dergelijke, zonder eigen intrinsieke betekenis of inherente eigenschap.

(2)

Minimaal domein.

Een stelling in de predikatenlogica kan via eem predicaat-toewijzing, of predicatie, verwijzen naar een aantal objecten (d.i. minstens één). In dat geval veronderstelt ze uiteraard het bestaan van minstens één verzameling bestaande uit minstens zoveel verschillende objecten als in de stelling worden onderscheiden: een zgn. 'minimaal domein' voor de stelling. Maar die verzameling hóeft natuurlijk niet te bestaan: allereerst niet in het abstracte domein, en nog minder in het empirische, fysische of welk ander domein ook. Dat heeft dan wel consequenties voor de mogelijkheid om de betreffende stelling 'waar te maken', anders gezegd, voor haar (waarheids)vervulbaarheid .

(3)

Interpretatie.

Voorafgaand aan interpretatie bestaat een bewering in de logica enkel uit een 'kale' syntactische structuur. Het doel van logica ligt in de mogelijkheid om de betekenis van beweringen en redeneringen eenduidig en bondig weer te geven in een logische structuur, zodat we vervolgens de gegeven voorstelling van zaken kunnen beoordelen op logische criteria.
In dat stadium kunnen redeneervormen overeenkomstig de wetten en regels van de logica beoordeeld worden op hun syntax: met name welgevormdheid; en hun semantiek: met name algemene geldigheid (validiteit). Dit blijkt mogelijk door te beslissen over louter de formele kenmerken van de logische structuur. Deze eigenschappen staan dus nog volkomen los van 'inhoud': elke interpretatie en elk referentieel domein.
Daarnaast kunnen we bij een gegeven logische structuur ook een betekenis zoeken. Natuurlijk kunnen we met een logische stelling pas iets van een inhoudelijke voorstelling van zaken weergeven nádat we haar een interpretatie hebben gegeven. In de

PDL

wijzen we daarbij een domein aan (bijvoorbeeld een bevolking), en geven aan waar de gebruikte codes voor objecten, predikaten en functies voor staan (bijvoorbeeld personen, werkwoorden en 'netwerkrelaties' tussen personen). Maar, met een inhoudelijke voorstelling van zaken hebben we natuurlijk nog niet automatisch een ware bewering.

(4)

Waarheidsvervulling.

Om nu een stelling in de taal van de

PDL

als waar te laten gelden dient allereerst aan één randvoorwaarde te worden voldaan: dat ze verenigbaar is met de toestand van het domein. Dit betekent dat aan minstens drie volgende eisen voldaan moet worden:

(a)

Consistentie.

De logische relaties in de stelling (vergelijkbaar met voegwoorden in de natuurlijke taal) en de verwijzingsrelaties van predikaten en functies leveren onderling geen contradictie op;
(b)

Voldoende omvang domein.

Het gekozen domein voor de variabelen en objecten is ruim genoeg;
(c)

Voldoende 'getuigen'.

Eventuele inhoudelijke aannamen over toestanden in het domein blijken juist, althans niet onmogelijk. Dat wil zeggen, er zijn in het domein voldoende 'getuigen' te vinden voor de grondinstanties van alle predicaties in de bewering of redenering.

(5)

Onafhankelijk van specifiek domein.

Op het syntactische niveau veronderstelt een logisch systeem - zoals

PPL

PDL

- alleen dat sommige verzamelingen kúnnen bestaan, van welke omvang ook, maar niet dàt ze ook daadwerkelijk bestaan. Daardoor kunnen we deze kale structuur in principe naar eigen goeddunken 'projecteren' op elk domein, concreet of abstract, reëel of fictief. De mate waarin de structuur past op het gekozen domein is mede beslissend voor de waarheidswaarde van die structuur volgens de logica.

Voor een waarheids-vervullende interpretatie - een zgn. model voor de betreffende stelling - is in ieder geval zoals gezegd een 'minimaal domein' nodig: een domein dat een voldoende aantal verschillende objecten bevat, om recht te doen aan de verscheidenheid en combinaties van objecten die de betreffende redenering veronderstelt. Het domein hoeft dus voor waarheids-vervulling alleen te voldoen aan een minimale omvang (c.q. kardinaliteit), oftewel een benedengrens.
Omgekeerd, als we aannemen dat een stelling - inclusief al haar predikaties - voor 'waar' kan doorgaan, nemen we per Implicatie aan dat het minimale domein ervoor inderdaad bestaat.
Hoe dan ook stelt zo'n stelling logisch gezien alleen 'minimale' kwantitatieve eisen aan het domein.
Maar voor waarheids-vervulling stelt de

PDL

geen bovengrens aan het domein. Een stelling in de

PDL

stelt dus geen enkele eis aan de maximale omvang, en zeker geen kwalitatieve eisen aan type , categorie of essentie en dergelijke van de objecten in het domein.
Kortom, elke stelling in de logica - dus ook de predikatenlogica - is volkomen onafhankelijk van welk specifiek domein of gebied van de werkelijkheid dan ook. Juist daardoor is de logica toepasbaar op elk willekeurig gebied van elke denkbare soort werkelijkheid of belevingswereld.

4.2. Axioma's voor de Predikatenlogica.

4.2.1. **Axioma's voor kwantoren.**

(0 : onwaar; ± : onbeslist; 1 : waar)

4.2.1.1. **Axioma's voor kwantoren, voor één variabele.**

Waarheidswaarden-tabel
PDL
.

Tabel van waarheidswaarden-combinaties van één-plaatsig

e

, gekwantificeerde formules.

Predikatenlogica: Waarheidswaarden-tabel
1	2	3	4	5	6	7
1	0	1	±	0	1	±
1	0	0	0	±	±	1
.T.	.F.	A		¬		¬
			x A(x)	x ¬A(x)	x A(x)	x ¬A(x)
			≡ ¬x ¬A(x)	≡ ¬x A(x)	≡ ¬x ¬A(x)	≡ ¬ x A(x)
			≡ ¬(7)	≡ ¬(6)	≡ ¬(5)	≡ ¬(4)

4.2.1.2. **Axioma's voor kwantoren, voor twee naar één variabele(n).**

Tabel tweewaardige waardencombinaties - met twee variabelen, geïnterpreteerd voor PPL, resp. PDL, resp. Sk
Nr.	Waarde- patroon				Logische relatie in PPL			Logische relatie in PDL		Logische relatie in Sk	Logische kracht
1	1	1	1	1	T	¬ F	X ¬ X				0
2	0	0	0	0	F	¬ T	X ¬ X				1
3	1	1	0	0	A ₁	¬¬ A ₁					0.50
4	1	0	1	0	A ₂	¬¬ A ₂					0.50
5	0	0	1	1	¬ A ₁	¬ A ₁					0.50
6	0	1	0	1	¬ A ₂	¬ A ₂					0.50
7	1	0	0	0	A ₁ A ₂	¬(¬ A ₁ ¬ A ₂)		x A [x]	¬x ¬ A [x]	A [x]	0.75
8	0	1	0	0	A ₁ ¬ A ₂	¬(¬ A ₁ A ₂)					0.75
9	0	0	1	0	¬ A ₁ A ₂	¬( A ₁ ¬ A ₂)					0.75
10	0	0	0	1	¬ A ₁ ¬ A ₂	¬( A ₁ A ₂)	A ₁ \ A ₂	¬x A [x]	x ¬ A [x]	¬ A [x]	0.75
11	1	1	1	0	A ₁ A ₂	¬(¬ A ₁ ¬ A ₂)		x A [x]	¬x ¬ A [x]	A [ c _s]	0.25
12	1	1	0	1	A ₁ ¬ A ₂	¬(¬ A ₁ A ₂)	A ₁ 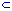A ₂				0.25
13	1	0	1	1	¬ A ₁ A ₂	¬( A ₁ ¬ A ₂)	A ₁ A ₂				0.25
14	0	1	1	1	¬ A ₁ ¬ A ₂	¬( A ₁ A ₂)	A ₁ \| A ₂	¬x A [x]	x ¬ A [x]	¬ A [ c _s]	0.25
15	1	0	0	1	A ₁ A ₂	¬( A ₁ # A ₂)					0.50
16	0	1	1	0	A ₁ # A ₂	¬( A ₁ A ₂)					0.50

4.2.1.3. **Axioma's voor kwantoren, en logische constanten en functies.**

Predikatenlogica: Waarheidswaarden-tabel
1	2	3	4	5	6	7	8	9
.T.	.F.	A	Negatief normaal vorm ( NNF )		Skolem constante	Instantiatie, universeel	Instantiatie, logische functie	Instantiatie, individueel (domein constante)
1	0	1	x A(x)	¬x ¬A(x)		_UI A(x)	_i A( f (x))	_i A( c )
1	0	0	x ¬A(x)	¬x A(x)		_UI ¬A(x)	_i ¬A( f (x))	_i ¬A( c )
1	0	±	x A(x)	¬x ¬A(x)	_Sk A( c _s)
1	0	±	x ¬A(x)	¬x A(x)	_Sk ¬A( c _s)

4.3. Basisprincipes voor formulebewerkingen in de Predikatenlogica (PDL).

4.3.1. **Geldige onderlinge afleidingsrelaties.**

Tussen variabelen, constanten en functies in de logica.
(m.b.t. predicaat 'A').

Identiteit tussen termen.

Wetten m.b.t. (non)identiteit van variabelen.

Triviaal: Alle variabele-namen verwijzen naar hetzelfde referentiële object als zijzelf.
(Dezelfde variabele-namen kunnen niet verwijzen naar verschillende referentiële objecten).

{

x (x

=

x ) }. Wet.

Wetten m.b.t. onderling afhankelijke predicaat-argumenten.

Cruciaal: Elke variabelenaam kan worden vervangen door een (onbepaalde) andere.
Dus verschillende variabelenamen x kunnen verwijzen naar dezelfde waarde (c.q. hetzelfde referentiële object in een domein).
Dus verschillende variabelenamen, zeg x en y, kunnen 'in werkelijkheid' onderling in waarde (d.i. semantisch) geheel of gedeeltelijk samenvallen.

y (x

=

y). Wet.

{D.w.z. y varieert hier over x, dus wordt beperkt tot minstens één individu/exemplaar per bijbehorende x, ongeacht haar waarde.}

y (A(x) ≡ A(y));

y (A(y ) ≡ A(x));

y (A(x)

A(y));

y (A(y)

A(x)).

Effect op logische kracht (in
PDL
).

Formule-derivaties - met degressie.

Logische kracht verloopt bij degressief afleiding van hoog (strikt, streng, scherp) naar laag (tolerant, zwak , vaag).

(1)

Verminderen van reikwijdte, generaliteit:

(1a)

Concretisering:

Via interpretatie van variabelen, m.n. instantiatie.
Is in feite: Conjunctieve reductie.

Bijv. (PPL): {A

_{(degres

)} A.
Bijv. (PDL): Universeel '

A(x)'

_{(
degres
)} individueel 'A(

c

_d)'
('

c

_d' kan een (bestaande) 'domein' constante zijn).

(2)

Verminderen van zekerheid.

Diffusie (vervagen).
Specifiek, definiet naar aspecifiek, indefiniet.
Via Disjunctief expansie.

Bijv. (PPL): {A}

_(degres
) (A

B).
Bijv. (PDL): Concreet 'A(

c

_d)'

_{(degres

)} existentieel '

A(x)';

_(Sk+1) 'A(

c

_s)'
('

c

_s' kan een (nieuwe) Skolem constante zijn).

(3)

Combinatie: Conjunct-disjunct reductie.

Resp. Conjunctieve reductie, Disjunctieve expansie.

(3a)

Conjunct-disjunct connectief reductie.

Bijv. (PPL): {A

_{(degres

)} A;

_(degres
) (A

B).

(3b)

Kwantor reductie: Particularisering.

Verzwakking van kwantificatie, d.i. reductie van kwantortype: kwantor-reductie (QR) (kwantor down-grading ).
Kan bijv. vanuit universele, singuliere of numerieke (k

≥

1) kwantor.

Bijv. (PDL): Universeel '

A(x)'

_{(
degres
)} concreet 'A(

c

_d)';

_(degres
) existentieel '

A(x)';

_(Sk+1) 'A(

c

_s)'.

(3c)

Factieve naar conditionele propositie.

Bijv. (PPL): (A

_{(degres

)} B;

_(degres
) (A

_(degres
) B).

4.3.2. Gradaties van logische kracht.

4.3.2.1. Eénplaatsige predicaties.

(1)

Zinnen met Universele kwantor.

Gradaties van logische kracht in universele kwantificatie.

In samengestelde formule.
Met Implicatie.
Stapsgewijze verzwakking van premisse(n).

(1)

Naar universele conclusie.

Sterkst:

y (A(x)

B(y)))';

x (A(x)

(

y B(y)))';

x A(x))

(

y B(y))';

'Als iets (x) een A is, dan zijn alle y tevens een B'.
Zwakker:

(1a)

y (A(x)

B(y))';

x (A(x)

(

y B(y)))';

'Er is een x, als die A is, dan zijn alle y een B'.
(1b) Of:

x (A(x)

B(x))';

'Als iets (x) een A is, dan is het tevens een B'.

(2)

Naar specifieke conclusie.

(2a) Zwakker:

x (A(x)

c

_d))';

'Er is een x, als die een A is, dan is

c

_d een B'.
(2b) Nog zwakker:

x (A(x)

c

_d))';

x A(x))

c

_d)';

'Als iets (x) een A is, dan is

c

een B'.
(2c) Zwakst:

x A(x))

c

_d)';

'Als elke x een A is, dan is

c

een B'.

(3)

Naar existentiële conclusie.

(3a) Zwakst:

y (A(x)

B(y))';

x (A(x)

(

y B(y)))';

x A(x))

(

y B(y))';

'Als iets (x) een A is, dan is een y tevens een B'.
(3b) Zwakker:

y (A(x)

B(y))';

x (A(x)

(

y B(y)))';

'Er is een x, als die A is, dan is er een y die B is'.
(3c) Zwakst:

x A(x))

(

y B(y))';

'Als elke (x) een A is, dan is een y tevens een B'.

4.3.2.2. Meerplaatsige predicatie s.

Formules met predikaten met minstens twee argumenten: 'Relatielogica', dyadische logica.

Notaties.

R : relaties 'op' een (sub)domein (verzameling)

D

_[m]^·n.
R^·r: een r-plaatsige relatie.
r : plaatsigheid, ariteit.
'R(x,y)': bijv. 'x is element of deel(verzameling) van y'.

4.3.2.2.1. **Meerplaatsige predicaties, universeel.**

(1)

Equivalentie van relatie(s).

(

y R(x,y) );

(

x R(x,y) );

_(UI) R(x,y).

'Voor elke x en elke y geldt R(x,y)'.
De {x,y} variëren hier dus over hun hele range vrij over elkaars range.
Bijv. een kruistabel, Cartesisch product, e.d..
Bijv. 'Elke x duwt elke y'.
Bijv. 'Elke baas betaalt elke knecht'.

Universele kwantor-volgordeverandering levert geen enkele verandering in betekens.
'Voor elke y en elke x geldt R(x,y)'.

Nb. Deze vorm wordt soms gebruikt - maar volkomen arbitrair - voor aanduiding van de passieve vorm van het gezegde in natuurlijke taal:
Bijv. 'Elke y wordt door elke x geduwd' (c.q. 'Elke x duwt elke y').
Bijv. 'Elke knecht wordt door elke baas betaald'.

(2)

Complementariteit van predicatie(s), universeel.

{

y R(x,y) }

¬(

y ¬R(x,y) );

#

(

y ¬R(x,y) ).

(3)

Inversie van relatie(s), universeel.

{

y R(x,y) }

:

(

y R(y,x) ) : inversie van R.

(4)

Symmetriciteit van relaties, universeel.

Betreft de richting van een relatie.
Symmetriciteit van een relatie kan volledig los staan van reflexiviteit van die relatie (zie aldaar).

y (R(x,y)

R(y,x))';
Relatie R is symmetrisch.

y (R(x,y)

R(y,x))';

y (R(x,y)

¬R(y,x))': Relatie R is asymmetrisch.

Relatie R is strikt bijectief.
D.w.z., er zijn alleen x die de relatie R (kunnen) hebben met y en vice versa.
Bijv.

bijectieve functie (bijectie):

één-één-duidige correspondentie, c.q. een-op-een correspondentie, tussen X en Y
(levert isomorfie).

{

y (R(x,y)

((

w (R(w,y)

=

x) )_w)

(

z (R(x,z)

=

z) )_z ) )_y,x }.

Bijv.: symmetrische Equivalentie, structural identity, congruentie, isomorfisme, correlatie =1.0.

(5)

Transitiviteit van relaties, universeel.

Betreft de richting van een relatie.

y (

z (R(x,z)

R(z,y)) _z

R(x,y))_y,x': Relatie R is transitief.
'

y (

z(R(x,z)

R(z,y)) _z

¬R(x,y))_y,x': Relatie R is atransitief.

(6)

Lineariteit van relaties, universeel.

Betreft de richting van een relatie.

y ((R(x,y)

R(y,x)

=

y ))': Relatie R is lineair.
'

y ¬((R(x,y)

R(y,x)

=

y ))'; Relatie R is a-lineair.

Bijv.:
'Niemand kijkt een gegeven paard in de bek;
en iemand geeft een paard aan een ander;
dan kijkt deze dat paard niet in de bek':
(mens: M, paard: P, geven door x van y aan z: G(x,y,z),
kijken door x van y in de bek K(x,y,

b

)):

z ((M(x)

P(y)

M(z,)

G(x,y,z))

¬K(z,y,

b

))'.

(7)

Afgeleiden.

(7a)

Unificatie binnen Literaal; via renaming.

Impliciet universele kwantor samenvoeging in Disjunctie.
Dus (hoogstens) geldig met degressie.

Bijv. (PDL,Sk): {R(x,y)}

[y:

=

x];

_(degres
)_(v) R(x,x) : is geldig onder voorwaarden.

(Mits {x,y} zijn vrije variabelen, ook buiten bereik van een externe kwantor).

_(UI^-1) (

x R(x ,x) );

(7b)

Reflexiviteit van relaties, universeel.

Ongeacht de richting van een relatie.
Voor alle (mogelijke) elementen geldt dat er een relatie is tussen dat element en zichzelf.
Reflexiviteit van een relatie kan geheel los staan van symmetriciteit van die relatie (zie aldaar).

Relatie R is reflexief toegepast.
Relatie R geldt (feitelijk, tenminste) reflexief.

{

x R(x,x) };

_(UI) R(x,x);

Dus elke x kan daarnaast de relatie R met een ander element, zeg y, hebben.
(Ongeacht context: m.a.w. andere kwantificaties van {x} mogen liggen binnen in het bereik van andere (externe) kwantoren).

Relatie R is (in principe, tenminste) reflexief.
Dus niet noodzakelijk strict.
Dus niet elke x hoeft de relatie R met zichzelf te hebben.
Maar: zodra een ding x een relatie heeft met een ding y, dan heeft x die relatie (in ieder geval) met zichzelf.
Dus: elke x kan daarnaast de relatie R met een ander element dan zichzelf hebben.

{

x (

y (R(x,y)

R(y,x) )_y

R(x ,x) )_x };

(

x (

y (R(x,y)

R(y,x) )

R(x,x) )_y )_x );

(

y ((R(x,y)

R(y,x) )

R( x,x) )_y,x );

(

y ((R(x,y)

R(x,x) )

(R( y,x)

R(x,x) ) )_x,y );

Relatie R is strikt reflexief.
M.a.w., kan uitsluitend reflexief gelden c.q. van toepassing zijn.
Dus: geen x kan de relatie R met een ander element dan zichzelf hebben.
D.w.z., er zijn geen x die de relatie R (kunnen) hebben met iets buiten zichzelf.

{

x (

y (R(x,y)

R(y,x) )

=

y) ) )_y )_x };

(

y ((R(x,y)

=

y) )

(R(y,x)

=

y) ) ) )_x,y );

Relatie R is (zeker) niet strict reflexief.
Dus: er is een x die de relatie R heeft met een ander element dan zichzelf.

{¬

x (

y (R(x,y)

R(y,x) )

=

y) ) )_y )_x };

(¬

y ((R(x,y)

=

y) )

(R(y,x)

=

y) ) ) )_x,y );

(

y ¬((R(x,y)

=

y) )

(R(y,x)

=

y) ) ) )_x,y );

(

y (¬(R(x,y)

=

y) )

¬(R(y,x)

=

y) ) ) )_x,y );

(

y ((R(x,y)

¬(x

=

y) )

(R(y,x)

¬(x

=

y ) ) ) )_x,y );

Relatie R geldt (wel, feitelijk) reflexief, maar (zeker) niet strict.
Dus elke x heeft zeker de relatie R met zichzelf; maar kan daarnaast de relatie R met een ander element dan zichzelf hebben.

{

x (R(x,x)

¬(

y ((R(x,y)

R(y,x ) )

=

y) )_y ) )_x };
(

x (R(x,x)

(¬

y ((R(x,y)

R(y,x ) )

=

y) )_y ) )_x );
(

x (R(x,x)

(

y ¬((R(x,y)

R(y,x ) )

=

y) )_y ) )_x );
(

x (R(x,x)

(

y ((R(x,y)

R(y,x ) )

¬(x

=

y) )_y ) )_x );

[*?]Vereist minstens twee domeinelementen.
Of moet voorwaardelijk, met Implicatie i.p.v. Conjunctie.

Relatie R is strict irreflexief.

{

x ¬R(x,x) }.

4.3.2.2.2. **Meerplaatsige predicaties, existentieel.**

(1)

Equivalentie van relatie(s).

(

y R(x,y) );

(

x R(x,y) );

_(Sk+1) R(

c

_s,

d

_s).

De {x,y} vormen hier dus twee afzonderlijke keuzes, d.i. (conjuncte) selecties, uit de hele range van de variabele(n).
'Voor sommige x en sommige y geldt R(x,y)'.
'Voor ≥ 1 x en voor ≥ 1 y geldt R(x,y)'.
Bijv. 'Minstens één x duwt minstens één y'.
Bijv. 'Minstens één baas betaalt minstens één knecht'.

Existentiële kwantor-volgordeverandering levert geen enkele verandering in betekens.
'Voor sommige y en sommige x geldt R(x,y)'.
'Voor ≥ 1 y en voor ≥ 1 x geldt R(x,y)'.

Nb. Deze vorm wordt soms gebruikt - maar volkomen arbitrair - voor aanduiding van de passieve vorm van het gezegde in natuurlijke taal:

Bijv. 'Minstens één y wordt door minstens één x geduwd'.
Bijv. 'Minstens één knecht wordt door minstens één baas betaald'.

(2)

Complementariteit van predicatie(s), existentieel.

{

y R(x,y) }

¬(

y ¬R(x,y) );

#

(

y ¬R(x,y) ).

(3)

Inversie van relatie(s), existentieel.

{

y R(x,y) }

:

(

y R(y,x) ) : inversie van R.

(4)

Symmetriciteit van relaties, existentieel.

y (R(x,y)

R(y,x))': Relatie R is niet-asymmetrisch.
'

y (R(x,y)

¬R(y,x))': Relatie R is niet-symmetrisch.

(5)

Transitiviteit van relaties, existentieel.

y (

z (R(x,z)

R(z,y ) )_z

¬R(x,y) )_y,x': Relatie R is niet-transitief.
'

y (

z(R(x,z)

R(z,y) ) _z

R(x,y) )_y,x': Relatie R is niet-atransitief.

(6)

Lineariteit van relaties, existentieel.

y ((¬R(x,y)

¬R(y,x)

¬(x

=

y))': Relatie R is niet-lineair.

(7)

Reflexiviteit van relaties, existentieel.

x ¬R(x,x)': Relatie R is niet-reflexief.
'

x R(x,x)': Relatie R is niet-irreflexief.

4.3.2.2.3. **Enkele relaties tussen relaties.**

Antisymmetrisch omvat asymmetrisch (maar niet omgekeerd).
M.a.w.: asymmetrisch impliceert antisymmetrisch (maar niet omgekeerd).
Diverse overige combinaties van relaties:

(·) Pre-orde: reflexief +transitief.
(·) Partiële orde: reflexief +transitief +antisymmetrisch.
(·) Strikt partiële orde: reflexief +transitief +asymmetrisch.
(·) Equivalentie: reflexief +transitief +symmetrisch.
(·) Totale orde: reflexief +transitief +antisymmetrisch +lineair.

4.3.2.2.4. Combinaties van Existentiële en Universele kwantor.

Kwantor-gestuurde verwijzingen en connectief-structuur.

Kwantor-volgorde, inter-argumentrelaties en connectief.
Kwantor-volgorde is in een Conjunctief-normaal vorm formule alleen [/soms] bepalend voor geldigheid als er minstens twee verschillende variabelen zijn die in minstens één en dezelfde predicaat-argumentenlijst tegelijk gebonden zijn aan verschillende kwantoren van verschillende kwantiteit.

(1)

'
E-U
' kwantor volgorde.

(1a)

x R(x,y)':

'Minstens één y bindt aan elke x zodat R(x,y) geldt'.
(Betreft niet noodzakelijk alle y).
Bijv. 'Minstens één y wordt door elke x geduwd'.
Bijv. 'Minstens één knecht wordt door elke baas betaald'.
(1b)

y R(x,y)':

'Minstens één x bindt aan elke y zodat R(x,y) geldt'.
(Betreft niet noodzakelijke alle x).
Bijv. 'Minstens één x duwt elke y'.
Bijv. 'Minstens één baas betaalt elke knecht'.

Onderlinge afleidbaarheid:

((1a)

(1b)):

ongeldig

.
Resolutie:

((

x R(x,y) )

¬(

y R(x,y) ) );
NNF:

((

x R(x,y) )

(

y ¬R(x,y) ) );
Skolemisatie:

_(Sk⁺²) (R(x,

c

_s)

¬R(x,

f

_s(x) ) ) :

niet

unificeerbaar.

((1b)

(1a)):

ongeldig

.
Resolutie:

((

y R(x,y) )

¬(

x R(x,y) ) );
NNF:

((

y R(x,y) )

(

x ¬R(x,y) ) );
Skolemisatie:

_(Sk⁺²) (R(

d

_s,y)

¬R(

g

_s(y),y) ) ) :

niet

unificeerbaar.

(2)

'
U-E
' kwantor volgorde.

(2a)

y R(x,y)':

'Voor elke x is er minstens één y zodat R(x,y) geldt'.
(Betreft dus niet noodzakelijk alle y).
Relatie R heeft voortzetting naar rechts (heeft linker inverse).

y : y varieert over x, dus wordt beperkt tot minstens één individu/exemplaar per bijbehorende x, ongeacht haar waarde.

Bijv. 'Elke x duwt minstens één y'.
Bijv. 'Elke baas betaalt minstens één knecht'.
(2b)

x R(x,y)':

'Voor elke y is er minstens één x zodat R(x,y) geldt'.
(Betreft dus niet noodzakelijke alle x).
Relatie R heeft voortzetting naar links (heeft rechter inverse).
Bijv.: 'Elke y wordt door minstens één x geduwd'.
'Elke knecht wordt door minstens één baas betaald'.

Onderlinge afleidbaarheid:

((2a)

(2b)):

ongeldig

.
Resolutie:

((

x R(x,y) )

¬(

y R(x,y) ) );
NNF:

((

x R(x,y) )

(

y ¬R(x,y) ) );
Skolemisatie:

_(Sk⁺²) (R(

f

_s(x),y )

¬R(

c

_s,y) ) :

niet

unificeerbaar.

((2b)

(2a)):

ongeldig

.
Resolutie:

((

y R(x,y) )

¬(

x R(x,y) ) );
NNF:

((

y R(x,y) )

(

x ¬R(x,y) ) );
Skolemisatie:

_(Sk⁺²) (R(x,

g

_s(x ) )

¬R(x,

d

_s) ) :

niet

unificeerbaar.

4.3.3. Diverse vertalingen naar de PDL

.

Vertalingen van beweringen naar formules in de predikatenlogica (

PDL

4.3.3.1. Simpele vertalingen naar de PDL

.

Bijv.: 'Er is een meisje M waar alle jongens J van houden'.

x (M(x)

y (J(y)

H(y,x)) ).

Bijv.: 'Alle jongens (J) houden van een meisje (M)'.
D.w.z. 'Elke jongen (J) houden van een meisje (M)'.

x (J(x)

y (M(y)

H(x,y)) ).

Bijv.: 'Iedereen (ieder persoon) houdt van iemand (minstens één persoon)'.

x (R(x)

y (A(y)

H(x,y)) ).

Bijv.: 'Voor alle x die P is, is er een y die Q is, zodat de relatie R van x naar y geldt.

x (P(x)

y (Q(y)

R(x,y)) ).

Bijv.: M: 'mens', K(x,y): 'kietelen door iets van iets'.

1. 'Wie zichzelf niet kietelt, wordt (wel) door een ander gekieteld'.

x ((M(x)

¬K(x,x))

y (M(y)

K(y,x))).

2. 'Wie zichzelf niet kietelt, wordt (stellig) niet door een ander gekieteld'.

x ((M(x)

¬K(x,x))

y (M(y)

K(y,x))).

3. 'Niemand die zichzelf niet kietelt, wordt door iedereen gekieteld'.

x ((M(x)

¬K(x,x))

y (M(y)

K(y,x))).

4. 'Iemand die zichzelf niet kietelt, kietelt niet iedereen'.

x ((M(x)

¬K(x,x))

y (M(y)

K(y,x))).

5. 'Iemand die zichzelf niet kietelt, wordt niet door iedereen gekieteld'.

x ((M(x)

¬K(x,x))

y (M(y)

K(y,x))).

4.3.3.2. Identiteit en Uniciteit.

(1)

Identiteit.

Bijv.: 'Alleen Aad zwemt'.
'Er is niemand die zwemt behalve Aad'.
(Lexicon: 'a' := Aad; 'Z' := zwemmen.)

(Z(

a

)

x (Z(x)

(x=

a

)) );

(Z(

a

)

x (Z(x)

¬(x=

a

)) ).

Bijv.: 'a houdt alleen van b':

(

x (H(

a

,x) ≡ (x=

b

)) ).
Bijv.: 'Alleen a houdt van b':

(

x (H(x,

b

) ≡ (x=

a

)) ).

Bijv.: 'a houdt van ieder behalve b':

(

x (H(

a

,x) ≡ ¬(x=

b

)) ).
Bijv.: 'Ieder houdt van a behalve b':

(

x (H(x,

a

) ≡ ¬(x=

b

)) ).
Bijv.: 'a houdt van b, maar b houdt van een ander':

(H(

a

b

)

(

x (H(

b

,x)

¬(x=

a

))) ).
Bijv.: 'a houdt van b, maar b houdt van een ander - en niet van

b

(H(

a

b

)

¬H(

b

a

)

(

x (H(

b

,x)

¬(x=

a

))) ).

Bijv.: 'Iedereen (ieder persoon) houdt van een ander (minstens één ander persoon)'.

(

x (A(x)

(

y (A(y)

¬(x

=

H(x,y ))_y))_x );

(

y (¬(x

=

H(x,y)) ).

Bijv.: 'Iemand (minstens één persoon) houdt van iedereen (ieder persoon)'.

(

x (A(x)

(

y (A(y)

H(x,y))_y))_x );

(

y H(x,y) ).

Bijv.: 'Iemand (minstens één persoon) houdt van ieder ander (ieder ander persoon)'.

(

x (A(x)

(

y (A(y)

¬(x

=

H(x,y ))_y))_x );

(

y (¬(x

=

H(x,y)) ).

(2)

Bepaald lidwoord.

(definiete determinator).

Bijv.: 'De A doet B'.

(

x (

y (A(y)

=

y))_y

B(x))_x ).

Bijv.: 'De A doet niet B':

(

x (

y (A(y)

=

y))_y

¬B(x))_x ).

(¬

x (

y (A(y) ≡ (x

=

y))_y

B(x))_x ).

Bijv.: 'Elke dokter behalve (dokter) Chris bezit een auto ).
(D: dokter-zijn, C: Chris-zijn, B: bezitten, A: auto-zijn).

(D(

c

_d)

(

x ((D(x)

¬(x=

c

_d))

y (A(y)

B(x,y)) ))

y (A(y)

c

_d,y)) ).

(3)

**Algemene functie.**

Niet toegestaan is: {(x1,y1),(x1,y2), ..}.

In causale analyse.

(1)

Verklaren.

Causale inferentie in retrospectief (via Controle- c.q. Baseline conditie).
Elke toestand B₁ is voldoende indicatie voor minstens één oorzaak A₁:

{

CE!

(x,y) _y, _x }.

{

y (B₁(y)

(

x (A₁(x)

CE!

(x,y) )_y) )_x }.

Bij verklaren:

Bijv. Controle op unieke bijdrage van oorzaken:
Geen (onbekende) disjuncte oorzaken.
Elk ding A₁ heeft een effect B₁ en elk effect B₁ heeft hoogstens één oorzaak A ₁:

{

y (

CE!

(x,y)

(

w (

CE!

(w,y)

=

w) )_w) )_y, _x }.

{

x (A₁(x)

(

y (B₁(y)

CE!

(x,y)

(

w (A₁(w)

(

CE!

(w,y)

=

w) ))_w) )_y) )_x }.

(2)

Voorspellen.

Voorspellen:
Causale inferentie in prospectief (via Experimentele conditie).
Elke toestand A₁ is voldoende indicatie voor minstens één effect B₁:

{

CE!

(x,y) _y, _x }.

{

x (A₁(x)

(

y (B₁(y)

CE!

(x,y) )_y) )_x }.

Bij voorspellen:

Bijv. Controle op beheersbaarheid van effecten:
Geen (onbekende) neven-effecten of disjuncte effecten.
Elk ding A₁ heeft een effect B₁ en elke oorzaak A₁ heeft hoogstens één effect B ₁:

{

y (

CE!

(x,y)

(

z (

CE!

(x,z)

=

z) )_z) )_y, _x }.

{

x (A₁(x)

(

y (B₁(y)

CE!

(x,y)

(

z (B₁(z)

(

CE!

(x,z)

=

z) ))_z) )_y) )_x }.

Bijv. Controle op zelfstandige bijdrage van oorzaken:
Geen (onbekende) noodzakelijke c.q. conjuncte voorwaarden.
Elk ding A₁ heeft een effect B₁, en naast A₁ is geen voorwaarde C₁ nodig voor effect B₁:

{

y (

CE!

(x,y)

(

z ((

w ((C₂(w)

(A₁(x)

C₁(z)) )

CE!

(w ,y) )_w )

(A₁(x)

C₁(z)) ) _z ) )_y, _x }.

{

y (

CE!

(x,y)

(

w ((C₂(w)

(A₁(x)

C ₁(z)) )

(

CE!

(w,y)

(A₁(x)

C₁(z)) ) )_w, _z ) )_y, _x }.

{

x (A₁(x)

(

y (B₁(y)

CE!

(x,y)

(

z (C₁(z)

((

w ((C₂(w)

(A₁(x)

C₁(z)) )

CE!

(w,y) )_w )

(A₁(x)

C₁(z )) ) )_z ) )_y ) )_x }.

{

x (A₁(x)

(

y (B₁(y)

CE!

(x,y)

(

z (C₁(z)

((

w ((C₂(w)

(A₁(x)

C₁(z)) )

(

CE!

(w,y)

(A₁(x)

C₁(z)) ) )_w ) )_z ) )_y ) )_x }.

4.3.3.3. Problemen in vertaling.

Van natuurlijke taal naar

PDL

.

De Existentiële kwantor verwijst niet noodzakelijk naar fysieke realia!
De referenten kunnen in het algemeen 'dingen' zijn die zich 'ergens' bevinden, in willekeurige welk domein: zoals bijv. logisch-abstracte of subjectief-mentale fenomenen.

Bijv.: 'Aad zoekt kabouters'.
Deze zin veronderstelt niet dat minstens één kabouter kan bestaan, in fysisch domein, maar sluit het ook niet uit.
Ze veronderstelt wèl dat de genoemde Aad, als agens van het zoeken, noodzakelijk moet veronderstellen dat minstens één kabouter kàn bestaan.
(

a

: Aad, Z: zoeken, K: kabouter-zijn).

(a)

(

x (K(x)

a

,x )) ).

Maar dat vooronderstelt: er bestaat werkelijk minstens één kabouter. Dit is niet wat de zin zegt.
(b)

(

x (K(x)

a

,x )) ).

Dit betekent: 'Als iets een kabouter is dan wordt die door Aad gezocht'.
Het 'iets' kan hier slaan op een fysisch, abstract of mentaal verschijnsel. Deze formule stelt het zoeken van Aad echter afhankelijk van het bestaan van een kabouter. Dat is niet wat de zin impliceert.
(c) Wellicht kunnen we een vooronderstelling expliciet maken:
Introduceer een impliciet predicaat 'vinden' (V).

(

x (Z(

a

,x)

(V(

a

,x)

K(x))) ).
D.w.z. Als Aad vindt wat hij zoekt, dan is dat een kabouter.

(d)

(

x (Z(

a

,x)

(

y ((x

=

K( y) )_y ) )_x ).

Deze oplossing heeft twee voordelen:

(1) Het zoeken dat

a

doet blijft een zelfstandig feit;
(2) Dat iets 'een kabouter is' blijft een open mogelijkheid.

(e) Mogelijke oplossing: voer de impliciete vooronderstelling expliciet in als voorwaardelijke stelling.
'Ad denkt (D) dat Kabouters te vinden (V) zijn':

(D(

a

, (

x (K(x)

V(x)) ) ).

'(Ad denkt (D) dat Kabouters te vinden (V) zijn), en hij zoekt ze':

(D(

a

, (

x (K(x)

V(x)) )

a

,x) ).

Cursus / training:

Methode Formele Logica

©

II. Basiswetten in de predicatenlogica.

4.

Semantiek voor Predikatenlogica.

4.1.

Interpretatie.

4.1.1.

Predikatenlogica en de opbouw van kennis.

4.1.2.

Relatie tussen syntax en betekenis van formules in de predikatenlogica.

Inhoudsvrije taal.

Minimaal domein.

Interpretatie.

PDL

Waarheidsvervulling.

PDL

Consistentie.

Voldoende omvang domein.

Voldoende 'getuigen'.

Onafhankelijk van specifiek domein.

PPL

PDL

PDL

PDL

4.2.

Axioma's voor de Predikatenlogica.

4.2.1.

Axioma's voor kwantoren.

4.2.1.1.

Axioma's voor kwantoren, voor één variabele.

Waarheidswaarden-tabel PDL.

PDL

e

Predikatenlogica: Waarheidswaarden-tabel

4.2.1.2.

Axioma's voor kwantoren, voor twee naar één variabele(n).

Tabel tweewaardige waardencombinaties - met twee variabelen, geïnterpreteerd voor PPL, resp. PDL, resp. Sk

PPL

PDL

Sk

T

F

X

X

F

T

X

X

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

^©

**Axioma's voor kwantoren.**

**Axioma's voor kwantoren, voor één variabele.**

Waarheidswaarden-tabel
PDL
.

**Axioma's voor kwantoren, voor twee naar één variabele(n).**

Tabel tweewaardige waardencombinaties
- met twee variabelen, geïnterpreteerd voor PPL, resp. PDL, resp. Sk

**Axioma's voor kwantoren, en logische constanten en functies.**

**Geldige onderlinge afleidingsrelaties.**

Effect op logische kracht (in
PDL
).