AlentoTraining & Advies-Arc of Essentials ©-drs. C.P. van der Velde-12-11-2015Dimensie/ vakgebied:LogicaCursus / training:Methode Formele Logica©Introductie Propositielogica (PPL)Uitgangspunten en richtlijnen.I.Opbouw van de propositielogica.De propositielogica (PPL) is het meest simpele systeem van formele logica. Het bevat de basisregels van de logica, die ten grondslag liggen aan vrijwel alle logische systemen van 'hogere' orde. Deze regels kunnen in principe heel bondig worden beschreven, pakweg op een half A4tje. Het vraagt vervolgens echter heel wat studie en oefening - dus tijd en moeite - om alle mogelijke combinaties en toepassingsvormen snel te kunnen herkennen, en te kunnen toetsen op hun geldigheid. In dit overzicht zijn zowel alle basisregels als alle elementaire toepassingsvormen expliciet vermeld. Bovendien wordt waar nodig het formele bewijs van hun geldigheid gegeven. Die geldt met name voor de regels die nodig zijn voor de belangrijkste bewijsmethoden in de propositielogica: met name de methode van waarheidswaardentabellen (Schröder-Peirce), van reductie naar waarheidswaarde ( Convergente reductie), van axiomatische bewijsvoering, van natuurlijke deductie ( Natural deduction, Gentzen-Fitch), van resolutie (Davis & Putnam, Robinson).
{N.b. Zie ook: Principes van Logische bewijsvoering
.}
De vermelde kenmerken en regelmatigheden zijn in principe toepasbaar op alle alledaagse taaluitingen en uitspraken, teksten, berichten, verhalen, of voorstellingen van zaken. Dit betekent dat je, nadat je het hele overzicht hebt doorgelezen, in principe elke redenering c.q. formule in de propositielogica - dat is elke uitspraak of gedachtestap met in de syntactische dieptestructuur minstens één elementaire bewering - kunt herkennen en kunt beoordelen op essentiële logische criteria zoals relevantie, consistentie en geldigheid. 1.Het kader van de propositielogicaElementaire beweringen.De regels van de propositielogica zijn allereerst van toepassing op het redeneren over elementaire beweringen. Een elementaire bewering is elk onderdeel van een hoeveelheid informatie dat nog afzonderlijk een zelfstandige bewering over iets (wat dan ook) kan vormen. Dat wil zeggen dat het zelfstandig een toedracht in een gebied van de werkelijkheid kan weerspiegelen. Het zijn dus betekeniselementen die niet louter een verwijzende functie hebben, maar die iets zeggen over een bepaald thema, direct of indirect, impliciet of expliciet. Redeneren met elementaire beweringenDe meest eenvoudige manier van redeneren is om alleen de waarheidsrelaties te bekijken tussen elementaire beweringen, dus voorbijgaand aan de betekenisstructuur binnen die elementaire beweringen. In de logica worden elementaire beweringen aangeduid als proposities. Het logische systeem voor het redeneren over proposities heet dan ook de propositielogica ( PPL).De grondslag voor dit systeem werd gelegd door de beroemde Griekse filosoof Aristotelis.
{Nb. Aristotelis (384-322 A.D.) was geboren in Stagira als zoon van Nicomachus, een bekende geneesheer.
Hij werd leerling van Plato aan de Academie van Athene,
werd leraar van Alexander de Grote aan het Macedonische hof en begon een eigen Lyceum.
Onder zijn belangrijkste werken zijn het Organum, bestaande uit zes verhandelingen over logica,
Physica, Metaphysica, De Anima, De Ethica, De Poetica, Rhetorica,
en een aantal werken over biologie en fysica. Hij stierf in Chalcis. }
1.1.Notaties.PPL: propositielogica. Als formeel logisch systeem.PPL* : De verzameling toegelaten uitdrukkingen (zinnen/ formules) vanPPL.1.2.Proposities en connectieven.
(1)
Elementaire beweringen in taal.Elementaire beweringen zijn de 'bouwstenen' van alle beweringen in een taal, ongeacht of dat een natuurlijke of kunstmatige taal is. In een taal weergegeven zijn elementaire beweringen de betekenisrepresentaties van zinnen en bijzinnen, oftewel alle taaleenheden die precies één zgn. gezegde bevatten. Elk gezegde bevat met name een hoofdwerkwoord. Dit laatste kan geformuleerd zijn in dynamische vorm, als proceswoord (lopen, praten, ..) of statische vorm, als nominalisatie (de loop, het gesprek, ..). Bij elk proceswoord hoort tenminste één ding dat het proces 'doet': de uitvoerder of agens (grammaticaal is dit het onderwerp van het gezegde in bedrijvende vorm). (2) Opbouw van redeneringenIn de PPLkan worden geredeneerd door elementaire beweringen - or atomaire proposities - te combineren, zodat we constellaties of ketens van redenering kunnen vormen, d.w.z. proposities van hogere complexiteit. Die combinaties zijn gebaseerd op logische relaties waaraan die beweringen kunnen worden verbonden.Neem bijvoorbeeld de zin: S: 'Jan slaat Piet met een hamer op zijn kop in de tuin als het regent bij de buren'. We benaderen deze zin hier vanuit het perspectief van de propositielogica ( PPL).(3) Componentenvan proposities.We brengen daarbij een onderscheid aan in elementaire beweringen (atomen) en voegwoorden ( connectieven).
(a)
Atomen:We bekijken eerst de elementaire beweringen zoals die in elke taal voorkomen. De elementaire beweringen vormen in de formele logica de atomaire formules (oftewel de enkelvoudige proposities) afgekort 'ATM'. Bijvoorbeeld, in de bovengenoemde zin S hebben we er twee: · A1: 'Jan slaat Piet met een hamer op zijn kop in de tuin'; · A2: 'het regent bij de buren'. Dus hier hebben we de verzameling: ATM* ={A1,A2}.(b) Connectieven:De logische verbindingen tussen proposities worden in het gewone spraakgebruik vaak gelegd door voegwoorden (als, dan, want, enz.). Die voegwoorden kunnen we in formele logica vertalen naar de connectieven. De connectieven vormen de logische structuur van de formule of redenering. Ze verwijzen naar de logische relaties die tussen beweringen worden aangegeven. Op het niveau van de logisch-semantische structuur worden ze ook wel operatoren of waarheidswaardefuncties genoemd, omdat ze bepalend zijn voor de waarheidswaarde van de betreffende stelling. In zin S hebben we de semantische structuur: S: '(P1 ALS P2)'. Het voegwoord 'als' kunnen we hier redelijk vertalen in het logische connectief de implicatie, aangeduid met het symbool '  '. '.Daarmee kijgen we als logisch-syntactische structuur: S: '(P2  P1)'. P1)'.1.3.Logische connectieven in PPL.De logische relaties kunnen worden herleid tot een klein aantal basisvormen, de logische connectieven. Hieronder volgt allereerst een overzicht van de belangrijkste connectieven die in de PPLgebruikt worden, met hun omschrijvingen en gangbare benamingen, hun tegenhangers in de natuurlijke taal (met name voegwoorden), en de symbolen die ervoor gebruikt worden bij vertalingen in formules volgens systemen voorPPLen hoger.Tabel 1.
Tabel 2.
Tabel 3.
Tabel 4.
Tabel 5.
2.Syntax voor propositielogica.2.1.Het alfabet van PPL.De verzameling symbolen van PPL.(1) De logische symbolen van |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 |
|---|---|
| 1 | 0 |
| 0 | 1 |
| T | F |
| A | ¬A |
| ¬B | B |
3.2.
Axioma's voor de propositielogica.
Waarheidswaarden-tabel voor logisch systeem.
Een waarheidswaardentabel bevat simpel gezegd alle mogelijke volgordes van waarheidswaarden bij de combinatie van n variabelen die elk v waarden kunnen aannemen.
3.2.1.
Axioma's voor één variabele.
Betreft enkelvoudige proposities oftewel elementaire beweringen.
(a) Waarheidswaarden-tabel
Deze waarheidswaardentabel bevat alle mogelijke volgordes van waarheidswaarden van ééne variabele (propositie) in de
De grondslag bestaat uit 1 variabele x 2 waarden = 2 basiscombinaties. Daarmee zijn 2 volgordes mogelijk, of reeksen van waarheidswaarden: waarvan elk een unieke logische relatie weergeeft. Hierdoor ontstaat de onderstaande meest eenvoudige tabel van 2 rijen bij 2 kolommen is 4 cellen.
Tabel 7.
(b)
Waarheidswaarden-tabel PPL
- voor één variabele.
Deze waarheidswaardentabel bevat alle mogelijke volgordes van waarheidswaarden van ééne variabele (propositie) in de
PPL
, die twee waarden kunnen aannemen.De grondslag bestaat uit 1 variabele x 2 waarden = 2 basiscombinaties. Daarmee zijn 2 volgordes mogelijk, of reeksen van waarheidswaarden: waarvan elk een unieke logische relatie weergeeft. Hierdoor ontstaat de onderstaande meest eenvoudige tabel van 2 rijen bij 2 kolommen is 4 cellen.
Tabel 7.
Waarheidswaarden |
||
|---|---|---|
1 |
± |
0 |
Waar,verum: Verificatie. |
Onbepaald,ongeïnterpreteerd: Indefiniet. |
Onwaar,falsum: Falsificatie. |
Waarheidswaarde(value, valor): |
||
$(G)=1. |
(0 <$(G)<1). |
$(G)=0. |
Waarheidswaardetoekenning(valuatie): |
||
|
V!(G) :=1. |
¬V!(G)  {0,1}. {0,1}. |
V!(G) :=0. |
Waarheidswaardebepaling(evaluatie), via eindig bewijs: |
||
 i E![i] i E![i]  G. G. |
(¬ i E![i] i E![i]  G) G)
 (¬ (¬ j E![j] j E![j]
 ¬G). ¬G). |
 i E![i] i E![i]  ¬G. ¬G. |
Interpretatie(denotatie, assignment): |
||
 m m M![m] G.
G. |
(¬ m m M![m] G)
G)  (¬ (¬ n n M![ n] ¬G). ¬G). |
 m m M![m] ¬
G. ¬
G. |
(b)
Basiswetten van de Aristotelische Logica.
(1) Wet van de Identiteit.
{'A'}
(2) Wet van de Equivalentie.=
'A'.
{A}  A.
A.
(3) Wet van het Uitgesloten Midden (Tertium non datur). A.
A.
{A}
(4) Wet van Uitgesloten Tegenstrijdigheid (Non contradictio).#
¬A.
{¬(A  ¬A)}.
¬A)}.
 ¬A)}.
¬A)}.3.2.2.
Axioma's voor twee variabelen.
(a) Waarheidswaarden-tabel
Deze waarheidswaardentabel bevat alle mogelijke volgordes van waarheidswaarden bij de combinatie van twee variabelen die elk twee waarden kunnen aannemen.
Deze uitgangsgegevens leveren allereerst 2 waarden keer 2 variabelen = 4 combinaties, oftewel mogelijke (individuele) objecttoestanden.
De grondslag voor de tabel bestaat uit 2 waarden tot de macht 2 variabelen = 4 toestandcombinaties, oftewel mogelijke domeintoestanden.
Daarmee zijn 2 tot de macht 4 = 16 volgordes mogelijk, of reeksen van waarheidswaarden, oftewel mogelijke (domein)toestandsrelaties, waarvan elk een unieke logische relatie weergeeft.
Hierdoor ontstaat de onderstaande tabel van 4 kolommen bij 16 rijen is 64 cellen.
Tabel 8.
Deze tabel - hoe hij ook wordt weergegeven - dekt hoe dan ook alle basiscombinaties die in het het meest elementaire begin van elke vorm van redenering een rol spelen. Ze vormt daardoor echt de allereerste, noodzakelijke grondslag voor correct combinatorisch denken.
De logische relaties die op deze wijze gedefinieerd zijn behoren tot het domein van abstracte patronen, oftewel van informatie: het informatiedomein.. Ze zijn hieraan gebonden, en vormen tegelijk de basisstructuur van dit domein.
Waarheidswaarden-tabel PPL
- voor twee variabelen.
Deze waarheidswaardentabel bevat alle mogelijke volgordes van waarheidswaarden bij de combinatie van twee variabelen die elk twee waarden kunnen aannemen.
Deze uitgangsgegevens leveren allereerst 2 waarden keer 2 variabelen = 4 combinaties, oftewel mogelijke (individuele) objecttoestanden.
De grondslag voor de tabel bestaat uit 2 waarden tot de macht 2 variabelen = 4 toestandcombinaties, oftewel mogelijke domeintoestanden.
Daarmee zijn 2 tot de macht 4 = 16 volgordes mogelijk, of reeksen van waarheidswaarden, oftewel mogelijke (domein)toestandsrelaties, waarvan elk een unieke logische relatie weergeeft.
Hierdoor ontstaat de onderstaande tabel van 4 kolommen bij 16 rijen is 64 cellen.
Tabel 8.
Tabel tweewaardige waardencombinaties |
||||||||
|---|---|---|---|---|---|---|---|---|
| Nr. | Waarde- patroon |
Logische relatie in PPL |
Logische kracht | |||||
| 1 | 1 | 1 | 1 | 1 |
T |
¬F |
X ¬ ¬X |
0 |
| 2 | 0 | 0 | 0 | 0 |
F |
¬T |
X ¬ ¬X |
1 |
| 3 | 1 | 1 | 0 | 0 |
A |
¬¬A |
0.50 | |
| 4 | 1 | 0 | 1 | 0 |
B |
¬¬B |
0.50 | |
| 5 | 0 | 0 | 1 | 1 |
¬A |
¬A |
0.50 | |
| 6 | 0 | 1 | 0 | 1 |
¬B |
¬B |
0.50 | |
| 7 | 1 | 0 | 0 | 0 |
A B |
¬(¬A ¬ ¬B) |
0.75 | |
| 8 | 0 | 1 | 0 | 0 |
A ¬ ¬B |
¬(¬A B) |
0.75 | |
| 9 | 0 | 0 | 1 | 0 |
¬A B |
¬(A ¬ ¬B) |
0.75 | |
| 10 | 0 | 0 | 0 | 1 |
¬A ¬ ¬B |
¬(A B) |
A\B |
0.75 |
| 11 | 1 | 1 | 1 | 0 |
A B |
¬(¬A ¬ ¬B) |
0.25 | |
| 12 | 1 | 1 | 0 | 1 |
A ¬ ¬B |
¬(¬A B) |
A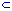 B |
0.25 |
| 13 | 1 | 0 | 1 | 1 |
¬A B |
¬(A ¬ ¬B) |
A B |
0.25 |
| 14 | 0 | 1 | 1 | 1 |
¬A ¬ ¬B |
¬(A B) |
A|B |
0.25 |
| 15 | 1 | 0 | 0 | 1 |
A B |
¬(A#B) |
0.50 | |
| 16 | 0 | 1 | 1 | 0 |
A#B |
¬(A B) |
0.50 | |
|
{Courtesy: Benjamin Peirce (1809-1880), Friedrich Wilheml Karl Ernst Schröder (1841-1902), e.a..} |
||||||||
|
{Zie: Bewijsmethode voor Propositielogica: de
Waarheidswaarden- tabelmethode.} |
||||||||
Deze tabel - hoe hij ook wordt weergegeven - dekt hoe dan ook alle basiscombinaties die in het het meest elementaire begin van elke vorm van redenering een rol spelen. Ze vormt daardoor echt de allereerste, noodzakelijke grondslag voor correct combinatorisch denken.
De logische relaties die op deze wijze gedefinieerd zijn behoren tot het domein van abstracte patronen, oftewel van informatie: het informatiedomein.. Ze zijn hieraan gebonden, en vormen tegelijk de basisstructuur van dit domein.
{Nb.
Vaak wordt gedacht dat voegwoorden uit de gewone taal 'vertaald' zijn in de formele logica en dat de waarheidswaardentabel hiervan een uitdrukking is. Het omgekeerde is echter het geval.
In de logica is eerst gekeken naar alle mogelijke combinaties van een minimale schaal van (binaire ) waarden (bijvoorbeeld waar en onwaar, ja en nee, aan en uit, enz.), en een aantal variabelen voor proposities (bijv. genaamd A en B). Deze combinaties kunnen worden weergegeven in de waarheidswaardentabel.
De 16 kolommen (reeksen) in de tabel vormen elk de definitie van één elementaire logische relatie in de
Uit deze formele, of beter 'combinatorische' definities van de logische voegwoorden, waaronder de materiële implicatie, volgen vervolgens noodzakelijk de elementaire semantische basiswetten in de logica.
De betekenis van de formele logische connectieven, waaronder de implicatie, wordt in de waarheidswaardentabel dus bepaald door de bijbehorende kolommen: met andere woorden, ze worden gedefinieerd door hun waarheidswaardenpatronen - en niet omgekeerd. Pas na deze formele definitie is bij elk patroon van waarheidswaarden een passende benaming gezocht, die zo dicht mogelijk ligt bij onderscheidingen die in de gewone taal gangbaar zijn.}
Vaak wordt gedacht dat voegwoorden uit de gewone taal 'vertaald' zijn in de formele logica en dat de waarheidswaardentabel hiervan een uitdrukking is. Het omgekeerde is echter het geval.
In de logica is eerst gekeken naar alle mogelijke combinaties van een minimale schaal van (binaire ) waarden (bijvoorbeeld waar en onwaar, ja en nee, aan en uit, enz.), en een aantal variabelen voor proposities (bijv. genaamd A en B). Deze combinaties kunnen worden weergegeven in de waarheidswaardentabel.
De 16 kolommen (reeksen) in de tabel vormen elk de definitie van één elementaire logische relatie in de
PPL
. Van die 16 reeksen zijn er 4 die de definitie vormen van een algemeen gangbaar connectief-symbool in dePPL
: '$
(1000)' voor conjunctie, '$
(1110)' voor disjunctie, '$
(1011)' voor implicatie en '$
(1001)' voor equivalentie. De overige 12 reeksen kunnen in deze vier connectieven vertaald worden - of omgekeerd, dat ligt maar aan je invalshoek.Uit deze formele, of beter 'combinatorische' definities van de logische voegwoorden, waaronder de materiële implicatie, volgen vervolgens noodzakelijk de elementaire semantische basiswetten in de logica.
De betekenis van de formele logische connectieven, waaronder de implicatie, wordt in de waarheidswaardentabel dus bepaald door de bijbehorende kolommen: met andere woorden, ze worden gedefinieerd door hun waarheidswaardenpatronen - en niet omgekeerd. Pas na deze formele definitie is bij elk patroon van waarheidswaarden een passende benaming gezocht, die zo dicht mogelijk ligt bij onderscheidingen die in de gewone taal gangbaar zijn.}
3.2.3.
Axioma's voor elk aantal variabelen.
(3.2.3.1)
Waarheidswaarden-tabel
Deze waarheidswaardentabel bevat alle mogelijke volgordes van waarheidswaarden bij de combinatie van elk aantal c.q. n variabelen die elk twee waarden kunnen aannemen. De grondslag bestaat uit 2 waarden tot de macht n variabelen = 2 **n basiscombinaties. Daarmee zijn 2 tot de macht 2 ** n = 2 **(2 **n ) volgordes mogelijk, of reeksen van waarheidswaarden: waarvan elk een unieke logische relatie weergeeft.
(3.2.3.2)
Voor elke willekeurige uitspraak over een logische relatie - een propositie - geldt een bepaald interpretatiebereik.
Dit bestaat uit een specifieke domeintoestand, een unieke waardencombinatie oftewel een waarheidswaardenpatroon.
Voorbeelden waarheidswaardentoekenning aan proposities.
'(..)': betekent in voorkomend geval "geordende reeks".
Bijvoorbeeld: "interpretatie", "interpretatiebereik", of "waarheidswaardepatroon".
Voorbeelden. De startkolommen voor n=1 atomen: {A} lopen als volgt, met (j:=1,n):
De startkolommen voor n=2 atomen: {A,B} lopen als volgt, met (j:=1,n);
zoals je n=2 loops genest laat lopen met (j :=1,2) en met (i[j] :=1,0):
Veel gebruikte waarheidswaardepatronen van twee-plaatsige proposities in twee-plaatsige waarheidswaardetabellen.
De startkolommen voor n=3 atomen: {A,B,C} lopen als volgt, met (j:=1,n);
zoals je n=3 loops genest laat lopen met (j :=1,3) en met (i[j] :=1,0):
Veel gebruikte waarheidswaardepatronen van twee-plaatsige proposities in drie-plaatsige waarheidswaardetabellen.
De startkolommen voor n=4 atomen: {A,B,C,D} lopen als volgt, met (j:=1,n);
zoals je n=4 loops genest laat lopen met (j :=1,4) en met (i[j] :=1,0):
(3.2.3.3)
Verschil rekenkundige en logische 'identiteit'.
Identiteit is soms symmetrisch: nl. met uitsluitend variabelen.
(3.2.3.4)
Logische tolerantie is de 'onzekerheid' die een bewering of redenering tot uitdrukking brengt.
Meer logische tolerantie betekent minder behoud van zekerheid, en meer verlies van informatieve waarde.
Staat tegenover logische kracht.
Tolerantiewaarden van connectieven per formule.
Bijvoorbeeld: in een tweewaardig (binair) systeem, met twee domeinelementen, geldt:
(3.2.3.5)
Het begrip logische kracht drukt de selectiviteit van beweringen of redeneringen uit.
Logische kracht is het selectief vermogen, de 'stelligheid' c.q. stringentie die een bewering of redenering tot uitdrukking brengt.
Meer logische kracht betekent meer behoud van zekerheid, en minder verlies van informatieve waarde.
"The amount of meaning can be measured.
It turns out that the less probable a message is, the more meaning it carries, which is entirely reasonable from the standpoint of our common sense." (Wiener, N., 1950).
Logische kracht - m.n. in de vorm van conjuncten - krijg je er moeilijk bij en raak je weer gemakkelijk kwijt.
Staat tegenover logische tolerantie.
Waarheidswaarden-tabel PPL
- voor n variabelen.
Deze waarheidswaardentabel bevat alle mogelijke volgordes van waarheidswaarden bij de combinatie van elk aantal c.q. n variabelen die elk twee waarden kunnen aannemen. De grondslag bestaat uit 2 waarden tot de macht n variabelen = 2 **n basiscombinaties. Daarmee zijn 2 tot de macht 2 ** n = 2 **(2 **n ) volgordes mogelijk, of reeksen van waarheidswaarden: waarvan elk een unieke logische relatie weergeeft.
(3.2.3.2)
Interpretatiebereik
Voor elke willekeurige uitspraak over een logische relatie - een propositie - geldt een bepaald interpretatiebereik.
Dit bestaat uit een specifieke domeintoestand, een unieke waardencombinatie oftewel een waarheidswaardenpatroon.
Voorbeelden waarheidswaardentoekenning aan proposities.
'(..)': betekent in voorkomend geval "geordende reeks".
Bijvoorbeeld: "interpretatie", "interpretatiebereik", of "waarheidswaardepatroon".
'A' heeft als interpretatiebereik:
'A B' heeft als interpretatiebereik:
B' heeft als interpretatiebereik:
'A B
B  C'
heeft als interpretatiebereik:
C'
heeft als interpretatiebereik:
$
(1,0).'A
 B' heeft als interpretatiebereik:
B' heeft als interpretatiebereik: $
(1,0,1,1).'A
 B
B  C'
heeft als interpretatiebereik:
C'
heeft als interpretatiebereik: $
(1,0,1,1,1,0,1,0).Voorbeelden. De startkolommen voor n=1 atomen: {A} lopen als volgt, met (j:=1,n):
j=1: A =
$
(10).De startkolommen voor n=2 atomen: {A,B} lopen als volgt, met (j:=1,n);
zoals je n=2 loops genest laat lopen met (j :=1,2) en met (i[j] :=1,0):
j=1: A =
j=2: B =
$
(1100).j=2: B =
$
(1010).Veel gebruikte waarheidswaardepatronen van twee-plaatsige proposities in twee-plaatsige waarheidswaardetabellen.
(A  B) =
B) =
(A B) =
B) =
(A B) =
B) =
 B) =
B) = $
(1000).(A
 B) =
B) = $
(1110).(A
 B) =
B) = $
(1011).De startkolommen voor n=3 atomen: {A,B,C} lopen als volgt, met (j:=1,n);
zoals je n=3 loops genest laat lopen met (j :=1,3) en met (i[j] :=1,0):
j=1: A =
j=2: B =
j=3: C =
$
(1111.0000).j=2: B =
$
(1100.1100).j=3: C =
$
(1010.1010).Veel gebruikte waarheidswaardepatronen van twee-plaatsige proposities in drie-plaatsige waarheidswaardetabellen.
(A  B) =
B) =
(A C) =
C) =
(B C) =
C) =
(A B) =
B) =
(A C) =
C) =
(B C) =
C) =
(A B) =
B) =
(A C) =
C) =
(B C) =
C) =
 B) =
B) = $
(1100.0000).(A
 C) =
C) = $
(1010.0000).(B
 C) =
C) = $
(1000.1000).(A
 B) =
B) = $
(1111.1100).(A
 C) =
C) = $
(1111.1010).(B
 C) =
C) = $
(1110.1110).(A
 B) =
B) = $
(1100.1111).(A
 C) =
C) = $
(1010.1111).(B
 C) =
C) = $
(1011.1011).De startkolommen voor n=4 atomen: {A,B,C,D} lopen als volgt, met (j:=1,n);
zoals je n=4 loops genest laat lopen met (j :=1,4) en met (i[j] :=1,0):
j=1: A =
j=2: B =
j=3: C =
j=4: D =
$
(11111111.00000000).j=2: B =
$
(11110000.11110000).j=3: C =
$
(11001100.11001100).j=4: D =
$
(10101010.10101010).(3.2.3.3)
Logische identiteit en valuatie.
'=' : "is gelijk aan", of "bedraagt" (logische identiteit).
'x
Anders gesteld: 'x
$
= 1' : "x is waar".Anders gesteld: 'x

$
1'.
'(p  q)
q) q) is onwaar". Anders gesteld: '(p
q) is onwaar". Anders gesteld: '(p  q)
q) 
'(m n)
n) y)
y) n)
n)  (x
(x
 y)'; oftewel:
y)'; oftewel:
((m n)
n) y)
y) ((m
((m  n)
n)
 (x
(x  y)).
y)).
 q)
q)$
= 0' : "(p q) is onwaar". Anders gesteld: '(p
q) is onwaar". Anders gesteld: '(p  q)
q) 
$
0'.'(m
 n)
n)$
= (x y)
y)$
' = '(m n)
n)  (x
(x
 y)'; oftewel:
y)'; oftewel:((m
 n)
n)$
= (x y)
y)$
) ((m
((m  n)
n)
 (x
(x  y)).
y)).Verschil rekenkundige en logische 'identiteit'.
'(x = 1)
(Eerste '=' is logische, tweede is rekenkundige identiteit).
Anders gesteld:
'(x = 1)
$
= 0' : "het feit dat x identiek is met 1, is onwaar".(Eerste '=' is logische, tweede is rekenkundige identiteit).
Anders gesteld:
'(x = 1)

$
0'.Identiteit is soms symmetrisch: nl. met uitsluitend variabelen.
'a = b'  'b = a'.
'b = a'.
'0 = a' : Alleen toegestaan als definitie ('0' geldt als 'a').
'a = 0' : geen wff: dubbelzinnig; kan betekenen:
'a
 'b = a'.
'b = a'.'0 = a' : Alleen toegestaan als definitie ('0' geldt als 'a').
'a = 0' : geen wff: dubbelzinnig; kan betekenen:
'a
$
= 0' (of 'a
$
0'), of '0 = a'.(3.2.3.4)
Logische tolerantie.
Logische tolerantie is de 'onzekerheid' die een bewering of redenering tot uitdrukking brengt.
Meer logische tolerantie betekent minder behoud van zekerheid, en meer verlies van informatieve waarde.
Staat tegenover logische kracht.
Tolerantiewaarden van connectieven per formule.
Bijvoorbeeld: in een tweewaardig (binair) systeem, met twee domeinelementen, geldt:
0.00 : falsum : { ¬A),
¬A),
0.25 : conjunctie : {(A B), (A
B), (A  ¬B), (¬A
¬B), (¬A  B), (¬A
B), (¬A  ¬B),
¬B),
0.50 : balans : {A, B, ¬A, ¬B, (A B), (A
B), (A
0.75 : disjunctie : {(A B), (A
B), (A  B), (¬A
B), (¬A  B), (¬A
B), (¬A  ¬B),
¬B),
1.00 : verum : { ¬A), (A
¬A), (A
 A), (B
A), (B  B),
B),
$
0, (A ¬A),
¬A), ..
}.0.25 : conjunctie : {(A
 B), (A
B), (A  ¬B), (¬A
¬B), (¬A  B), (¬A
B), (¬A  ¬B),
¬B), ..
}.0.50 : balans : {A, B, ¬A, ¬B, (A
 B), (A
B), (A #
B),..
}.0.75 : disjunctie : {(A
 B), (A
B), (A  B), (¬A
B), (¬A  B), (¬A
B), (¬A  ¬B),
¬B), ..
}.1.00 : verum : {
$
1, (A ¬A), (A
¬A), (A
 A), (B
A), (B  B),
B), ..
}.(3.2.3.5)
Logische kracht.
Het begrip logische kracht drukt de selectiviteit van beweringen of redeneringen uit.
Logische kracht is het selectief vermogen, de 'stelligheid' c.q. stringentie die een bewering of redenering tot uitdrukking brengt.
Meer logische kracht betekent meer behoud van zekerheid, en minder verlies van informatieve waarde.
"The amount of meaning can be measured.
It turns out that the less probable a message is, the more meaning it carries, which is entirely reasonable from the standpoint of our common sense." (Wiener, N., 1950).
Logische kracht - m.n. in de vorm van conjuncten - krijg je er moeilijk bij en raak je weer gemakkelijk kwijt.
Staat tegenover logische tolerantie.
3.3.
Basisprincipes voor formulebewerkingen in de Propositielogica (PPL).
Een logische operatie is een omzetting of bewerking van een logische formule - een bewering of redenering.
Ze is te beschouwen als de (verkorte, formele) weergave van een 'denkstap' in een redenering.
Redenering omvat afleiding.
Een redenering - of meer algemeen, een denkproces - kunnen we in het algemeen opvatten als een proces van informatieverwerking met twee fasen: (a) het combineren van bekende gegevens, en (b) het daaruit afleiden van andere gegevens.
3.3.1.
Formulebewerkingen (derivaties).
Een 'afleiding', c.q. formule-afleiding (derivatie): vormt een logische operatie die de éne verzameling van (één of meer) logische beweringen omzet in een andere verzameling van (één of meer) logische beweringen. Een afleiding vormt daarmee de kern van elke redenering.
Een geldige logische afleiding garandeert behoud van waarheid.
We kunnen in redeneringen gegevens afleiden via twee typen logische relaties: equivalentie (tweezijdig, symmetrisch) en implicatie (éénzijdig, asymmetrisch).
Daarbij is equivalentie simpelweg een combinatie van twee implicaties.
3.3.2.
Effecten op Logische kracht.
Een geldige logische afleiding levert behoud of vermindering van logische kracht.
Logische kracht verloopt bij degressief afleiding van hoog (strikt, streng, scherp) naar laag (tolerant, zwak, vaag).
Effect van logische afleiding op logische kracht kan zijn:
gelijk (parafrase), verlaagd (degressie), onbepaald (contingent-ongeldigheid), of verspeeld (inconsistent-ongeldigheid, contradictie).
Hieruit volgen algemene vuistregels bij logische afleiding.
• Altijd toegestaan: mogelijkheden, dus onzekerheden toevoegen (tenzij het tegendeel blijkt).
• Nooit toegestaan: zekerheid toevoegen (tenzij het bewijs blijkt).
• Nooit toegestaan: zekerheid toevoegen (tenzij het bewijs blijkt).
Praktische binaire rekenregel.
De waarheidswaardepatronen van de premisse(n) in een redenering 'tellen op' tot één samenvattend waarheidswaardepatroon, die de most general unifier, of MGU, van die premisse(n) vormt.
(In conjunctie is dit een minimum, in disjunctie is dit een maximum waarde).
• Onder parafrase (equivalentie) is de resultante voor elke bit exact 'gelijk aan'
het waarheidswaardepatroon van de totale conclusie in de redenering.
Bijv.: {(A  B
B  (¬(¬A
(¬(¬A
 ¬B) }
¬B) }  (
(
• Onder degressie (implicatie 'proper') is de resultante voor minstens één bit
'vermeerderd', en anders exact 'gelijk aan', het waarheidswaardepatroon van de totale conclusie
in de redenering. B
B  (¬(¬A
(¬(¬A
 ¬B) }
¬B) }  (
($
(1000)
$
(1000) ).
Bijv.: {(A  B
B  (
( B) }
B) }  (
( (
(
 B
B  (
(degres
) (A B) }
B) }  (
($
(1000) (
(degres
)$
(1110) ).
(3.3.2.1)
(3.3.2.2)
Conservatief-validiteit.
(zekerheid, garantie).
D.i. Equivalentie in engere zin, Semantische equivalentie.
(3.3.2.3)
Uitbreiding, divergentie:
(a)
Betreft aantal formele middelen, taalelementen.
(b)
Bettreft aantal formele elementen, c.q. aantal mogelijke referenten, reikwijdte):
vermeerdering van logische kracht; versterking:
(c)
Syntactisch [- serieel]: introductie, (syntactische) extensie.
Betreft aantal formele middelen, taalelementen.
Bijv.: 'A'  'A, X'.
'A, X'.
 'A, X'.
'A, X'.(b)
Semantisch [- conjunctief]: (semantische) expansie, illogisme.
Bettreft aantal formele elementen, c.q. aantal mogelijke referenten, reikwijdte):
vermeerdering van logische kracht; versterking:
(b1)
Pseudo-parafrase.
Bijv.: {A}  B.
B.
: is
(b2)  B.
B.: is
ongeldig
.Pseudo-degressie.
Bijv.: {A}  (A
(A  B).
B).
: is
 (A
(A  B).
B).: is
ongeldig
.(c)
Semantisch [- disjunctief]: betekenisdivergentie: ambiguïteit.
(3.3.2.2)
Parafrase: Behoud van Logische kracht.
Conservatief-validiteit.
(zekerheid, garantie).
D.i. Equivalentie in engere zin, Semantische equivalentie.
Hoofdvorm van geldige parafrase inferentie.
'x  y' : Synonymie van syntactische constructies.
y' : Synonymie van syntactische constructies.
(zie 2.1 (1d2) Referentiële identiteit).
De selectiviteit van x is altijd gelijk aan die van y.
D.w.z.: bij een logische afleiding kan geen verlies van logische kracht plaatsvinden.
' (
(
Voor extrapolatie naar Predikatenlogica (PDL): y' : Synonymie van syntactische constructies.
y' : Synonymie van syntactische constructies.(zie 2.1 (1d2) Referentiële identiteit).
De selectiviteit van x is altijd gelijk aan die van y.
D.w.z.: bij een logische afleiding kan geen verlies van logische kracht plaatsvinden.
'
 (
(parafrase
)' : afleiding geldig onder equivalentie, dus met parafrase, behoud van Logische kracht.
' (u)' : equivalentie geldig onder argumenten-unificatie.
(u)' : equivalentie geldig onder argumenten-unificatie.
 (u)' : equivalentie geldig onder argumenten-unificatie.
(u)' : equivalentie geldig onder argumenten-unificatie.
(a)
Herhaling: reïteratie.
(b)
Logische equivalentie.
Syntactisch: structuurovereenkomst; symmetrie, isomorfie.
Herhaling: reïteratie.
Bijv.: 'A, X'  'A, X, X'.
'A, X, X'.
 'A, X, X'.
'A, X, X'.(b)
Semantisch: betekenisovereenkomst; equivalentie, parafrase, synonymie .
Logische equivalentie.
Bijv. (PPL): {¬(A  B) ≡ (¬A
B) ≡ (¬A  ¬B)}.
¬B)}.
Bijv. (PDL): {A(x) ≡ A(y)}.
 B) ≡ (¬A
B) ≡ (¬A  ¬B)}.
¬B)}.
Bijv. (PDL): {A(x) ≡ A(y)}.
(3.3.2.3)
Degressie: Vermindering van Logische kracht.
Hoofdvormen van geldige degressie inferentie.
(a)
(b)
D.i. Reductie in engere zin, vermindering van logische kracht; verzwakking.
Logische kracht, selectiviteit: van hoog (strikt, streng, scherp) naar laag (tolerant, zwak, vaag).
Syntactisch: syntactische reductie; deletie, eliminatie, comprimatie.
Bijv.: 'A, X'  'A'.
'A'.
 'A'.
'A'.(b)
Semantisch: semantische reductie, degressie.
D.i. Reductie in engere zin, vermindering van logische kracht; verzwakking.
Logische kracht, selectiviteit: van hoog (strikt, streng, scherp) naar laag (tolerant, zwak, vaag).
(b1)
Richten, selecteren. Vermindering van logische kracht (verzwakking).
Logische implicatie.
Richten, selecteren. Vermindering van logische kracht (verzwakking).
(b1a)
Particularisering, Concretisering:
Via conjunctief reductie.
Verminderen van reikwijdte, generaliteit.
Particularisering, Concretisering:
Via conjunctief reductie.
Bijv. (PPL): {A  X}
X}  A.
A.
(b1b)
Diffusie (vervagen).
Via disjunctief expansie.
Toevoeging van mogelijkheden (beschikbare opties). Vermindering van logische kracht (verzwakking).
Creatief denken, leiden (afstemmen, daarna sturen).
Via disjunct introductie.
(b1c) Combinatie.
M.n. conjunct-disjunct connectief reductie (kwantor down-grading).
 X}
X}  A.
A.
(b1b)
Verminderen van zekerheid.
Diffusie (vervagen).
Via disjunctief expansie.
Toevoeging van mogelijkheden (beschikbare opties). Vermindering van logische kracht (verzwakking).
Creatief denken, leiden (afstemmen, daarna sturen).
Via disjunct introductie.
Bijv. (PPL): {A}  (A
(A  X).
X).
Bijv. (PPL): {A B)}
B)}  (A
(A
 B
B  X).
X).
Bijv. (PPL): {A B}
B}  ((A
((A
 B)
B)  X).
X).
 (A
(A  X).
X).Bijv. (PPL): {A
 B)}
B)}  (A
(A
 B
B  X).
X).Bijv. (PPL): {A
 B}
B}  ((A
((A
 B)
B)  X).
X).(b1c) Combinatie.
M.n. conjunct-disjunct connectief reductie (kwantor down-grading).
Bijv. (PPL): {A  B}
B}  (
( (
( B).
B).
O.a. Factieve naar conditionele propositie. B}
B}  (
(degres
) A; (
(degres
) (A B).
B).
Bijv. (PPL): (A  B)
B)  (
( (
( (
(
 B)
B)  (
(degres
) B; (
(degres
) (A (
(degres
) B).III. Regels voor formulebewerkingen in de Propositielogica
Herschrijfregels: Regels voor transformatie onder parafrase/ equivalentie.
Behoud van logische kracht.
Parafrase: vindt plaats bij een logisch geldige afleiding met behoud van logische kracht.
Afleiding, met parafrase (semantische equivalentie): met behoud van logische kracht.
Transformatie:
Afleiding naar andere syntactische structuur, zonder verlies van logische kracht.
D.w.z. 'andere vorm, maar altijd dezelfde (onverminderde) inhoud'.
4.
Enkelvoudige transformaties van het hoofdconnectief, onder parafrase/ equivalentie.
4.1.
Enkelvoudige transformaties van het hoofdconnectief - Tabel.
(4.1a)
Tabel 9.
Omzettings-tabel voor conjunctie, disjunctie en implicatie.
Tabel 9.
| x |
|
|
|
|
|---|---|---|---|---|
& |
v |
> |
< |
|
A
|
 .. |
 ¬(¬A ¬(¬A  ¬B) ¬B)
|
 ¬(A ¬(A  ¬B) ¬B)
|
 ¬(B ¬(B  ¬A) ¬A)
|
A
|
 ¬(¬A ¬(¬A  ¬B) ¬B)
|
 .. |
 (¬A (¬A  B) B)
|
 (¬B (¬B  A) A)
|
A
|
 ¬(A ¬(A  ¬B) ¬B)
|
 (¬A (¬A  B) B)
|
 (¬B (¬B  ¬A) ¬A)
|
 (B (B 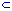 A) A)
|
A
|
 ¬(¬A ¬(¬A  B) B)
|
 (A (A  ¬B) ¬B)
|
 (B (B  A) A)
|
 (¬B (¬B 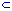 ¬A) ¬A)
|
4.2.
Enkelvoudige transformaties van het hoofdconnectief - per Type connectief.
Regels voor omzetting van het hoofdconnectief.
4.2.1.
Basiswaarden (valenties).
(a)
Altijd ware bewering (tautologie; validiteit).
Nimmer ware bewering (falsum, contradictio)
Waarheid, geldigheid.
Altijd ware bewering (tautologie; validiteit).
{ ((A
((A  ¬A) : Tertium non datur, Law of excluded middle.
¬A) : Tertium non datur, Law of excluded middle.
 ((A
((A  ¬A)
¬A)
 (B
(B  ¬B)).
¬B)).
(b) $
(1111)} ((A
((A  ¬A) : Tertium non datur, Law of excluded middle.
¬A) : Tertium non datur, Law of excluded middle. ((A
((A  ¬A)
¬A)
 (B
(B  ¬B)).
¬B)).Onwaarheid, contradictie.
Nimmer ware bewering (falsum, contradictio)
{ ((A
((A  ¬A) : Law of noncontradiction.
¬A) : Law of noncontradiction.
 ((A
((A  ¬A)
¬A)
 (B
(B  ¬B)).
¬B)).
$
(0000)} ((A
((A  ¬A) : Law of noncontradiction.
¬A) : Law of noncontradiction. ((A
((A  ¬A)
¬A)
 (B
(B  ¬B)).
¬B)).4.2.2.
Enkelvoudige formules (atomen).
(a)
Enkelvoudige formule; A Onafhankelijk van B.
(a1)
(b)
{ A;
A;
 ¬(¬A ).
¬(¬A ).
(a2)$
(1100)} A;
A;
 ¬(¬A ).
¬(¬A ).
{ ¬A;
¬A;
 ¬( A ).
¬( A ).
$
(0011)} ¬A;
¬A;
 ¬( A ).
¬( A ).Enkelvoudige formule; B Onafhankelijk van A.
(b1)
{ B;
B;
 ¬(¬B ).
¬(¬B ).
(b2)$
(1010)} B;
B;
 ¬(¬B ).
¬(¬B ).
{ ¬B;
¬B;
 ¬( B ).
¬( B ).
$
(0101)} ¬B;
¬B;
 ¬( B ).
¬( B ).4.2.3.
Conjuncties.
(Zgn. 'Alpha' formules).
(a)
(Eenvoudige) Conjunctie.
{ ( A
( A  B);
B);
 ¬(¬A
¬(¬A  ¬B);
¬B);
 ¬( A
¬( A  ¬B);
¬B);
 ¬( B
¬( B  ¬A);
¬A);
 ¬( A | B);
¬( A | B);  ¬(¬A \ ¬B).
¬(¬A \ ¬B).
(b)$
(1000)} ( A
( A  B);
B);
 ¬(¬A
¬(¬A  ¬B);
¬B);
 ¬( A
¬( A  ¬B);
¬B);
 ¬( B
¬( B  ¬A);
¬A);
 ¬( A | B);
¬( A | B);  ¬(¬A \ ¬B).
¬(¬A \ ¬B).
{ ( A
( A  ¬B);
¬B);
 ¬(¬A
¬(¬A  B);
B);
 ¬( A
¬( A  B);
B);
 ¬(¬B
¬(¬B  ¬A);
¬A);
 ¬( A | ¬B);
¬( A | ¬B);  (¬A \ B).
(¬A \ B).
(c)$
(0100)} ( A
( A  ¬B);
¬B); ¬(¬A
¬(¬A  B);
B);
 ¬( A
¬( A  B);
B);
 ¬(¬B
¬(¬B  ¬A);
¬A);
 ¬( A | ¬B);
¬( A | ¬B);  (¬A \ B).
(¬A \ B).
{ (¬A
(¬A  B);
B);
 ¬( A
¬( A  ¬B);
¬B);
 ¬(¬A
¬(¬A  ¬B);
¬B);
 ¬( B
¬( B  A);
A);
 ¬(¬A | B);
¬(¬A | B);  ( A \ ¬B).
( A \ ¬B).
(d) $
(0010)} (¬A
(¬A  B);
B);
 ¬( A
¬( A  ¬B);
¬B);
 ¬(¬A
¬(¬A  ¬B);
¬B);
 ¬( B
¬( B  A);
A);
 ¬(¬A | B);
¬(¬A | B);  ( A \ ¬B).
( A \ ¬B).Gelijktijdige afwezigheid (parallelle negatie), 'NOR'.
{ (¬A
(¬A  ¬B);
¬B);
 ¬( A
¬( A  B);
B);
 ¬(¬A
¬(¬A  B);
B);
 ¬(¬B
¬(¬B  A);
A);
 ¬(¬A | ¬B);
¬(¬A | ¬B);  ( A \ B);
( A \ B);
 (A NOR B).
(A NOR B).
$
(0001)} (¬A
(¬A  ¬B);
¬B); ¬( A
¬( A  B);
B);
 ¬(¬A
¬(¬A  B);
B);
 ¬(¬B
¬(¬B  A);
A);
 ¬(¬A | ¬B);
¬(¬A | ¬B);  ( A \ B);
( A \ B); (A NOR B).
(A NOR B).4.2.4.
(Inclusieve) Disjuncties, c.q. implicaties.
(Zgn. 'Bèta' formules).
(a)
Rule of inference. Productieregel.
(Eenvoudige) Disjunctie (alternatie).
{ ( A
( A  B);
B);
 ¬(¬A
¬(¬A  ¬B);
¬B);
 (¬A
(¬A  B);
B);
 (¬B
(¬B  A);
A);
 (¬A | ¬B);
(¬A | ¬B);  ¬( A \ B).
¬( A \ B).
(b)$
(1110)} ( A
( A  B);
B);
 ¬(¬A
¬(¬A  ¬B);
¬B);
 (¬A
(¬A  B);
B);
 (¬B
(¬B  A);
A);
 (¬A | ¬B);
(¬A | ¬B);  ¬( A \ B).
¬( A \ B).
{ ( A
( A  ¬B);
¬B);
 ¬(¬A
¬(¬A  B);
B);
 (¬A
(¬A  ¬B);
¬B);
 (B
(B  A);
A);
 (¬A | B);
(¬A | B);  ¬( A \ ¬B).
¬( A \ ¬B).
(c) $
(1101)} ( A
( A  ¬B);
¬B); ¬(¬A
¬(¬A  B);
B);
 (¬A
(¬A  ¬B);
¬B);
 (B
(B  A);
A);
 (¬A | B);
(¬A | B);  ¬( A \ ¬B).
¬( A \ ¬B).(Materiële) Implicatie.
Rule of inference. Productieregel.
{ (¬A
(¬A  B);
B);
 ¬( A
¬( A  ¬B);
¬B);
 ( A
( A  B);
B);
 (¬B
(¬B  ¬A);
¬A);
 ( A | ¬B);
( A | ¬B);  ¬(¬A \ B).
¬(¬A \ B).
(d) $
(1011)} (¬A
(¬A  B);
B);
 ¬( A
¬( A  ¬B);
¬B);
 ( A
( A  B);
B);
 (¬B
(¬B  ¬A);
¬A);
 ( A | ¬B);
( A | ¬B);  ¬(¬A \ B).
¬(¬A \ B).Uitgesloten samenvoeging (incompatibiliteit, Exclusie), NAND.
{ (¬A
(¬A  ¬B);
¬B);
 ¬( A
¬( A  B);
B);
 ( A
( A  ¬B);
¬B);
 (B
(B  ¬A);
¬A);
 ( A | B);
( A | B);  ¬(¬A \ ¬B);
¬(¬A \ ¬B);
 (A NAND B).
(A NAND B).
$
(0111)} (¬A
(¬A  ¬B);
¬B); ¬( A
¬( A  B);
B);
 ( A
( A  ¬B);
¬B);
 (B
(B  ¬A);
¬A);
 ( A | B);
( A | B);  ¬(¬A \ ¬B);
¬(¬A \ ¬B); (A NAND B).
(A NAND B).4.2.5.
Equivalentie.
(Materiële) Equivalentie.
Parafrase, synonimie. 'Alle termen zijn tegelijk waar, of alle termen zijn tegelijk onwaar'.
(a)
Tweeplaatsig:
{
 ( A
( A  B);
B);
 (¬A
(¬A  ¬B);
¬B);
 ¬( A
¬( A  ¬B);
¬B);
 ¬(¬A
¬(¬A  B);
B);
 ¬( A
¬( A  ¬(¬A
¬(¬A  ( A
( A
 (¬A
(¬A
 ( ( A
( ( A  B)
B)
 ( B
( B  A) );
A) );
 ( (¬A
( (¬A  ¬B)
¬B)
 (¬B
(¬B  ¬A) );
¬A) );
 ( ( A
( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) );
 ( (¬A
( (¬A  B)
B)
 (¬B
(¬B  A) );
A) );
 ( ( A
( ( A  ¬B)
¬B)
 ( B
( B  ¬A) );
¬A) );
 ( (¬A
( (¬A  B)
B)
 ( A
( A  ¬B) );
¬B) );
 (¬( A
(¬( A  ¬B)
¬B)
 ¬( B
¬( B  ¬A) );
¬A) );
 (¬(¬A
(¬(¬A  B)
B)
 ¬(¬B
¬(¬B  A) );
A) );
 (¬( A
(¬( A  ¬B)
¬B)
 ¬(¬A
¬(¬A  B) );
B) );
 ¬( ( A
¬( ( A  ¬B)
¬B)
 ( B
( B  ¬A) );
¬A) );
 ¬( (¬A
¬( (¬A  B)
B)
 (¬B
(¬B  A) );
A) );
 ¬( ( A
¬( ( A  ¬B)
¬B)
 (¬A
(¬A  B) );
B) );
 ( ( A
( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) );
 ¬(¬( A
¬(¬( A  B)
B)
 ¬(¬A
¬(¬A  ¬B) );
¬B) );
 ¬( (¬A
¬( (¬A  ¬B)
¬B)
 ( A
( A  B) );
B) );
 ¬( ( A
¬( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) );
(b) $
(1001)} ( A
( A  B);
B);
 (¬A
(¬A  ¬B);
¬B);
 ¬( A
¬( A  ¬B);
¬B);
 ¬(¬A
¬(¬A  B);
B); ¬( A
¬( A #
B); ¬(¬A
¬(¬A #
¬B); ( A
( A
#
¬B); (¬A
(¬A #
B); ( ( A
( ( A  B)
B)
 ( B
( B  A) );
A) );
 ( (¬A
( (¬A  ¬B)
¬B)
 (¬B
(¬B  ¬A) );
¬A) );
 ( ( A
( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) ); ( (¬A
( (¬A  B)
B)
 (¬B
(¬B  A) );
A) );
 ( ( A
( ( A  ¬B)
¬B)
 ( B
( B  ¬A) );
¬A) );
 ( (¬A
( (¬A  B)
B)
 ( A
( A  ¬B) );
¬B) ); (¬( A
(¬( A  ¬B)
¬B)
 ¬( B
¬( B  ¬A) );
¬A) );
 (¬(¬A
(¬(¬A  B)
B)
 ¬(¬B
¬(¬B  A) );
A) );
 (¬( A
(¬( A  ¬B)
¬B)
 ¬(¬A
¬(¬A  B) );
B) ); ¬( ( A
¬( ( A  ¬B)
¬B)
 ( B
( B  ¬A) );
¬A) );
 ¬( (¬A
¬( (¬A  B)
B)
 (¬B
(¬B  A) );
A) );
 ¬( ( A
¬( ( A  ¬B)
¬B)
 (¬A
(¬A  B) );
B) ); ( ( A
( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) ); ¬(¬( A
¬(¬( A  B)
B)
 ¬(¬A
¬(¬A  ¬B) );
¬B) ); ¬( (¬A
¬( (¬A  ¬B)
¬B)
 ( A
( A  B) );
B) ); ¬( ( A
¬( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) );Meerplaatsig:
{
 ( A
( A  B
B
 C);
C);
 ¬( A
¬( A
 (¬A
(¬A  ¬B
¬B
 ¬C);
¬C);
 ¬(¬A
¬(¬A
 ( ( A
( ( A  B)
B)
 ( B
( B  C)
C)
 ( C
( C  A) );
A) );
 ( (¬A
( (¬A  B)
B)
 (¬B
(¬B  C)
C)  (¬C
(¬C  A) );
A) );
 ( ( A
( ( A  B
B
 C)
C)  (¬A
(¬A
 ¬B
¬B  ¬C) );
¬C) );
 ¬(¬( A
¬(¬( A  B
B
 C)
C)  ¬(¬A
¬(¬A
 ¬B
¬B  ¬C) );
¬C) );
 ¬( (¬A
¬( (¬A  ¬B
¬B
 ¬C)
¬C)  ( A
( A
 B
B  C) );
C) );
 ¬( ( A
¬( ( A  B
B
 C)
C)  (¬A
(¬A
 ¬B
¬B  ¬C) );
¬C) );
$
(1000.0001)} ( A
( A  B
B
 C);
C); ¬( A
¬( A #
B#
C); (¬A
(¬A  ¬B
¬B
 ¬C);
¬C); ¬(¬A
¬(¬A #
¬B#
¬C); ( ( A
( ( A  B)
B)
 ( B
( B  C)
C)
 ( C
( C  A) );
A) ); ( (¬A
( (¬A  B)
B)
 (¬B
(¬B  C)
C)  (¬C
(¬C  A) );
A) ); ( ( A
( ( A  B
B
 C)
C)  (¬A
(¬A
 ¬B
¬B  ¬C) );
¬C) ); ¬(¬( A
¬(¬( A  B
B
 C)
C)  ¬(¬A
¬(¬A
 ¬B
¬B  ¬C) );
¬C) ); ¬( (¬A
¬( (¬A  ¬B
¬B
 ¬C)
¬C)  ( A
( A
 B
B  C) );
C) ); ¬( ( A
¬( ( A  B
B
 C)
C)  (¬A
(¬A
 ¬B
¬B  ¬C) );
¬C) );4.2.6.
Exclusief-disjunctie.
Antivalentie.
'Geen van de termen zijn tegelijk waar, en geen van de termen zijn tegelijk onwaar'.
(a)
Tweeplaatsig:
{
 ( A
( A  (¬A
(¬A  ¬( A
¬( A  ¬(¬A
¬(¬A
 ¬( A
¬( A  B);
B);
 ¬(¬A
¬(¬A  ¬B);
¬B);
 ( A
( A  ¬B);
¬B);
 (¬A
(¬A  B);
B);
 ( ( A
( ( A  ¬B)
¬B)
 (¬B
(¬B  A) );
A) );
 ( (¬A
( (¬A  B)
B)
 ( B
( B  ¬A) );
¬A) );
 ( ( A
( ( A  ¬B)
¬B)
 (¬A
(¬A  B) );
B) );
 ( (¬A
( (¬A  ¬B)
¬B)
 ( B
( B  A) );
A) );
 ( ( A
( ( A  B)
B)
 (¬B
(¬B  ¬A) );
¬A) );
 ( (¬A
( (¬A  ¬B)
¬B)
 ( A
( A  B) );
B) );
 (¬( A
(¬( A  B)
B)
 ¬(¬B
¬(¬B  ¬A) );
¬A) );
 (¬(¬A
(¬(¬A  ¬B)
¬B)
 ¬( B
¬( B  A) );
A) );
 (¬( A
(¬( A  B)
B)
 ¬(¬A
¬(¬A  ¬B) );
¬B) );
 ¬( ( A
¬( ( A  B)
B)
 (¬B
(¬B  ¬A) );
¬A) );
 ¬( (¬A
¬( (¬A  ¬B)
¬B)
 ( B
( B  A) );
A) );
 ¬( ( A
¬( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) );
 ¬( ( A
¬( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) );
 (¬( A
(¬( A  B)
B)
 ¬(¬A
¬(¬A  ¬B) );
¬B) );
 ( (¬A
( (¬A  ¬B)
¬B)
 ( A
( A  B) );
B) );
 ( ( A
( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) );
(b) $
(0110)} ( A
( A #
B); (¬A
(¬A #
¬B); ¬( A
¬( A #
¬B); ¬(¬A
¬(¬A #
B); ¬( A
¬( A  B);
B);
 ¬(¬A
¬(¬A  ¬B);
¬B);
 ( A
( A  ¬B);
¬B);
 (¬A
(¬A  B);
B); ( ( A
( ( A  ¬B)
¬B)
 (¬B
(¬B  A) );
A) );
 ( (¬A
( (¬A  B)
B)
 ( B
( B  ¬A) );
¬A) );
 ( ( A
( ( A  ¬B)
¬B)
 (¬A
(¬A  B) );
B) ); ( (¬A
( (¬A  ¬B)
¬B)
 ( B
( B  A) );
A) );
 ( ( A
( ( A  B)
B)
 (¬B
(¬B  ¬A) );
¬A) );
 ( (¬A
( (¬A  ¬B)
¬B)
 ( A
( A  B) );
B) ); (¬( A
(¬( A  B)
B)
 ¬(¬B
¬(¬B  ¬A) );
¬A) );
 (¬(¬A
(¬(¬A  ¬B)
¬B)
 ¬( B
¬( B  A) );
A) );
 (¬( A
(¬( A  B)
B)
 ¬(¬A
¬(¬A  ¬B) );
¬B) ); ¬( ( A
¬( ( A  B)
B)
 (¬B
(¬B  ¬A) );
¬A) );
 ¬( (¬A
¬( (¬A  ¬B)
¬B)
 ( B
( B  A) );
A) );
 ¬( ( A
¬( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) ); ¬( ( A
¬( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) ); (¬( A
(¬( A  B)
B)
 ¬(¬A
¬(¬A  ¬B) );
¬B) ); ( (¬A
( (¬A  ¬B)
¬B)
 ( A
( A  B) );
B) ); ( ( A
( ( A  B)
B)
 (¬A
(¬A  ¬B) );
¬B) );Meerplaatsig:
{
 ( A
( A
 ¬( A
¬( A  B
B
 C);
C);
 (¬A
(¬A
 ¬(¬A
¬(¬A  ¬B
¬B
 ¬C);
¬C);
 ¬( ( A
¬( ( A  B)
B)
 ( B
( B  C)
C)
 ( C
( C  A) );
A) );
 ( ( A
( ( A  ¬B)
¬B)
 ( B
( B  ¬C)
¬C)
 ( C
( C  ¬A) );
¬A) );
 ¬( ( A
¬( ( A  B
B
 C)
C)  (¬A
(¬A
 ¬B
¬B  ¬C) );
¬C) );
 (¬( A
(¬( A  B
B
 C)
C)  ¬(¬A
¬(¬A
 ¬B
¬B  ¬C) );
¬C) );
 ( (¬A
( (¬A  ¬B
¬B
 ¬C)
¬C)  ( A
( A
 B
B  C) );
C) );
 ( ( A
( ( A  B
B
 C)
C)  (¬A
(¬A
 ¬B
¬B  ¬C) );
¬C) );
$
(0111.1110)} ( A
( A #
B#
C); ¬( A
¬( A  B
B
 C);
C); (¬A
(¬A #
¬B#
¬C); ¬(¬A
¬(¬A  ¬B
¬B
 ¬C);
¬C); ¬( ( A
¬( ( A  B)
B)
 ( B
( B  C)
C)
 ( C
( C  A) );
A) ); ( ( A
( ( A  ¬B)
¬B)
 ( B
( B  ¬C)
¬C)
 ( C
( C  ¬A) );
¬A) ); ¬( ( A
¬( ( A  B
B
 C)
C)  (¬A
(¬A
 ¬B
¬B  ¬C) );
¬C) ); (¬( A
(¬( A  B
B
 C)
C)  ¬(¬A
¬(¬A
 ¬B
¬B  ¬C) );
¬C) ); ( (¬A
( (¬A  ¬B
¬B
 ¬C)
¬C)  ( A
( A
 B
B  C) );
C) ); ( ( A
( ( A  B
B
 C)
C)  (¬A
(¬A
 ¬B
¬B  ¬C) );
¬C) );Echter:
{
 ( ( A
( ( A  ( B
( B  ( C
( C
$
(0000.0000)} ( ( A
( ( A #
B) ( B
( B #
C) ( C
( C #
A) );4.3.
Semantische volledigheid van connectieven.
De gehele (semantische) verzameling van logische relaties in
PPL
kan intensioneel c.q. axiomatisch worden gedefinieerd met een beperkte selectie uit de (syntactische) verzameling van connectieven.We kennen een aantal voorbeelden van minimale complete verzamelingen van axioma's gesteld in implicatie.
(4.3.1)
Met de onderstaande drie regels wordt de hele semantiek van de PPL gedefinieerd.
Deze worden hier vermeld ter kennisneming, en om mee te oefenen.
Deze axiomatisering wordt zelden gebruikt in de praktijk.
Per stelling wordt een toepassing gegeven van de bewijsmethode van Convergente parafrase reductie, die erg handig is in de praktijk om logische geldigheid te toetsen.
(4.3.2)
Stel de welgevormde formules van
Semantische volledigheid van implicatie.
Met de onderstaande drie regels wordt de hele semantiek van de PPL gedefinieerd.
Deze worden hier vermeld ter kennisneming, en om mee te oefenen.
Deze axiomatisering wordt zelden gebruikt in de praktijk.
Per stelling wordt een toepassing gegeven van de bewijsmethode van Convergente parafrase reductie, die erg handig is in de praktijk om logische geldigheid te toetsen.
(1) {A
 (B
(B  A)}:
A)}:
 ( ¬A
( ¬A  (¬B
(¬B
 A) );
A) );
 ( (
( ( ¬B );
¬B );
 (
(
(2) {(A
 (B
(B  C))
C))
 ((A
((A  B)
B)
 (A
(A  C))}:
C))}:
 ( ¬(¬A
( ¬(¬A  (¬B
(¬B
 C))
C))  (¬(¬A
(¬(¬A
 B)
B)  (¬A
(¬A  C)) );
C)) );
 ( ¬(¬A
( ¬(¬A  ¬B
¬B
 C)
C)  ((A
((A  ¬B)
¬B)  ¬A
¬A  C) );
C) );
 ( (A
( (A  B
B
 ¬C)
¬C)  (A
(A  ¬B)
¬B)  ¬A
¬A  C );
C );
 ( (B)
( (B)  (¬B)
(¬B)
 ¬A
¬A  C );
C );
 ( (
( ( ¬A
¬A
 C );
C );
 (
(
(3) {(A
 B)
B)  ((¬B
((¬B
 A)
A)  B)}:
B)}:
 ( (¬A
( (¬A  B)
B)
 ((B
((B  A)
A)
 B) );
B) );
 ( ¬(¬A
( ¬(¬A  B)
B)
 (¬(B
(¬(B  A)
A)  B) );
B) );
 ( (A
( (A  ¬B)
¬B)
 ((¬A
((¬A  ¬B)
¬B)
 B) );
B) );
 ( (A
( (A  (¬A
(¬A
 ¬B)
¬B)  B)
B)  (¬B
(¬B  (¬A
(¬A  ¬B)
¬B)
 B) );
B) );
 ( (A
( (A  ¬B
¬B
 B)
B)  (¬B
(¬B  B) );
B) );
 ( (A
( (A 
 (
(
 ( (
( (
 (
(
 (B
(B  A)}:
A)}: ( ¬A
( ¬A  (¬B
(¬B
 A) );
A) ); ( (
( ($
1) ¬B );
¬B ); (
($
1). (B
(B  C))
C))
 ((A
((A  B)
B)
 (A
(A  C))}:
C))}: ( ¬(¬A
( ¬(¬A  (¬B
(¬B
 C))
C))  (¬(¬A
(¬(¬A
 B)
B)  (¬A
(¬A  C)) );
C)) ); ( ¬(¬A
( ¬(¬A  ¬B
¬B
 C)
C)  ((A
((A  ¬B)
¬B)  ¬A
¬A  C) );
C) ); ( (A
( (A  B
B
 ¬C)
¬C)  (A
(A  ¬B)
¬B)  ¬A
¬A  C );
C ); ( (B)
( (B)  (¬B)
(¬B)
 ¬A
¬A  C );
C ); ( (
( ($
1) ¬A
¬A
 C );
C ); (
($
1). B)
B)  ((¬B
((¬B
 A)
A)  B)}:
B)}: ( (¬A
( (¬A  B)
B)
 ((B
((B  A)
A)
 B) );
B) ); ( ¬(¬A
( ¬(¬A  B)
B)
 (¬(B
(¬(B  A)
A)  B) );
B) ); ( (A
( (A  ¬B)
¬B)
 ((¬A
((¬A  ¬B)
¬B)
 B) );
B) ); ( (A
( (A  (¬A
(¬A
 ¬B)
¬B)  B)
B)  (¬B
(¬B  (¬A
(¬A  ¬B)
¬B)
 B) );
B) ); ( (A
( (A  ¬B
¬B
 B)
B)  (¬B
(¬B  B) );
B) ); ( (A
( (A 
$
1) (
($
1) ); ( (
( ($
1)
$
1 ); (
($
1).(4.3.2)
Semantische volledigheid van negatie, van conjunctie, van disjunctie .
Stel de welgevormde formules van
PPL
zijn WFF* = {F, G,..
}.
(a)
Voor elke F bestaat er een G zodat F semantisch equivalent is aan F,
terwijl G uitsluitend gebruikt maakt van connectieven {¬, ,
,
 }.
}.
(In dat geval staat G in disjunctief normaal vorm (
M.a.w.: de verzameling {¬, ,
,  } is
semantisch volledig.
} is
semantisch volledig.
(b)
Ook geldt: de verzameling {¬, } is semantisch volledig.
} is semantisch volledig.
(c)
Wanneer negatie en conjunctie worden gecombineerd tot de NAND operator '|' (Sheffer stroke) dan volgt:
De verzameling {|} is semantisch volledig.
Axiomatisering met drie connectieven
Voor elke F bestaat er een G zodat F semantisch equivalent is aan F,
terwijl G uitsluitend gebruikt maakt van connectieven {¬,
 ,
,
 }.
}.(In dat geval staat G in disjunctief normaal vorm (
DNF
) en/of conjunctief normaal vorm (CNF
); voorDNF
,DNF
conversies zie deel VI , H.9).M.a.w.: de verzameling {¬,
 ,
,  } is
semantisch volledig.
} is
semantisch volledig.(b)
Axiomatisering met twee connectieven
Ook geldt: de verzameling {¬,
 } is semantisch volledig.
} is semantisch volledig.(c)
Axiomatisering met NAND.
Wanneer negatie en conjunctie worden gecombineerd tot de NAND operator '|' (Sheffer stroke) dan volgt:
De verzameling {|} is semantisch volledig.
{F}  ((F | F) | (F | F)).
((F | F) | (F | F)).
{¬F} (F | F).
(F | F).
{F G}
G}  ¬(F |
G)
¬(F |
G)  ((F | G) | (F | G)).
((F | G) | (F | G)).
{F G}
G}  (¬F
| ¬G)
(¬F
| ¬G)  ((F | F) | (G | G)).
((F | F) | (G | G)).
{F G}
G}  (F
| ¬G)
(F
| ¬G)  (F | (F | G)).
(F | (F | G)).
{F G}
G}  ((F
| ¬G)
((F
| ¬G)  (G | ¬F))
(G | ¬F))
 ( ((F | (F | G)) | (G | (G | F
))) | ((F | (F | G)) | (G | (G | F))) ).
( ((F | (F | G)) | (G | (G | F
))) | ((F | (F | G)) | (G | (G | F))) ).
 ((F | F) | (F | F)).
((F | F) | (F | F)).{¬F}
 (F | F).
(F | F).{F
 G}
G}  ¬(F |
G)
¬(F |
G)  ((F | G) | (F | G)).
((F | G) | (F | G)).{F
 G}
G}  (¬F
| ¬G)
(¬F
| ¬G)  ((F | F) | (G | G)).
((F | F) | (G | G)).{F
 G}
G}  (F
| ¬G)
(F
| ¬G)  (F | (F | G)).
(F | (F | G)).{F
 G}
G}  ((F
| ¬G)
((F
| ¬G)  (G | ¬F))
(G | ¬F))
 ( ((F | (F | G)) | (G | (G | F
))) | ((F | (F | G)) | (G | (G | F))) ).
( ((F | (F | G)) | (G | (G | F
))) | ((F | (F | G)) | (G | (G | F))) ).IV. Wetten voor logische Normaal Vorm conversies [I].
Syntactische standaardisatie.
Een logische 'normaal vorm', of 'canonische vorm', is een gestandaardiseerd schema voor de schrijfwijze (syntax) van logische formules.
5.
Parafrase via Syntactische verandering: binding (Associatief).
Bindingverandering c.q. Nestingverandering (Associatief).
Syntactische verandering zonder (syntactische) termreductie;
zonder (semantische) verandering van hoofdconnectief, en zonder (semantisch) verlies van logische kracht.
Bijv. t.b.v. standaardisatie, via (maximale) reductie van syntactische complexiteit door middel van Nesting vereenvoudiging.
5.1. Syntactische bindingskracht van connectieven.
De connectieven binden - althans volgens gebruik - van sterk naar zwak in de volgorde:
{ ¬,  ,
,  ,
,  ,
,
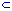 ,
,  ,
,
 }.
}.
 ,
,  ,
,  ,
,
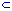 ,
,  ,
,
 }.
}.Als het hoofdconnectief-type van een formule geldt alléén het connectief met de minste bindingskracht.
Bijv.: '¬A  B
B  C
C
 D
D  E
E
mag herschreven en/of geïnterpreteerd worden in geneste structuur als:
'(((((¬A) B)
B)  C )
C )
 D )
D )  E )
E )
Bijv.: 'A C
C  D
D
 E
E  ¬F' :
¬F' :
mag worden herschreven en/of geïnterpreteerd als:
'A (C
(C  (D
(D
 (E
(E  (¬F)))))'.
(¬F)))))'.
 B
B  C
C
 D
D  E
E #
F' :mag herschreven en/of geïnterpreteerd worden in geneste structuur als:
'(((((¬A)
 B)
B)  C )
C )
 D )
D )  E )
E ) #
F).'Bijv.: 'A
#
B C
C  D
D
 E
E  ¬F' :
¬F' :mag worden herschreven en/of geïnterpreteerd als:
'A
#
(B (C
(C  (D
(D
 (E
(E  (¬F)))))'.
(¬F)))))'.De bindingsregels hebben dus geen inherente logische geldingskracht, maar louter een conventionele gebruikswaarde.
Ze hebben als nadeel dat cruciale syntactische structuurkenmerken impliciet blijven, waardoor steeds extra herleiding (aandacht, inspanning) nodig is om de eigenlijke syntactische structuur te achterhalen, wat weinig doelmatig is en ook de kans op fouten verhoogt.
Het is daarom functioneel om als regel alle nestingrelaties expliciet te maken.
Voor zo'n strikt eenduidige vorm van wff kunnen we een afzonderlijke notatie invoeren:
'wff+' : welgevormde formule, strikt eenduidig.
Dat wil zeggen, per (sub)formule is er één soort of type hoofdconnectief.
Bijv.: 'A  Q' : wff+.
Q' : wff+.
Bijv.: 'A Q
Q  x' : wff+.
x' : wff+.
Bijv.: 'A Q
Q  x' : wff, niet wff
+; betekent impliciet 'A
x' : wff, niet wff
+; betekent impliciet 'A  (Q
(Q  x)'.
x)'.
Bijv.: 'A (Q
(Q  x)' : wff, èn wff
+.
x)' : wff, èn wff
+.
 Q' : wff+.
Q' : wff+.Bijv.: 'A
 Q
Q  x' : wff+.
x' : wff+.Bijv.: 'A
 Q
Q  x' : wff, niet wff
+; betekent impliciet 'A
x' : wff, niet wff
+; betekent impliciet 'A  (Q
(Q  x)'.
x)'.Bijv.: 'A
 (Q
(Q  x)' : wff, èn wff
+.
x)' : wff, èn wff
+.5.2. Symmetrie en associatie.
{  ,
,  ,
,
 ,
,  } : zijn symmetrisch
en daardoor Associatief.
} : zijn symmetrisch
en daardoor Associatief.
 ,
,  ,
,
 ,
,  } : zijn symmetrisch
en daardoor Associatief.
} : zijn symmetrisch
en daardoor Associatief.5.3. Nestingverandering per hoofdconnectief.
(5.3.1)
Symmetrie geldt niet voor implicatie { } en zijn inverse variant {
} en zijn inverse variant {
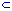 }.
}.
In Conjunctie.
Bijv.: {A  B
B  C}
C}
 ((A
((A  B)
B)  C).
C).
Bijv.: {A B
B  C}
C}
 (A
(A  (B
(B  C)).
C)).
Bijv.: {(A B)
B)  C}
C}
 (A
(A  (B
(B  C)).
C)).
Bijv.: {A (B
(B  C)}
C)}
 ((A
((A  B)
B)  C).
C).
(5.3.2)  B
B  C}
C}
 ((A
((A  B)
B)  C).
C).Bijv.: {A
 B
B  C}
C}
 (A
(A  (B
(B  C)).
C)).Bijv.: {(A
 B)
B)  C}
C}
 (A
(A  (B
(B  C)).
C)).Bijv.: {A
 (B
(B  C)}
C)}
 ((A
((A  B)
B)  C).
C).In Disjunctie.
Bijv.: {A  B
B  C}
C}
 ((A
((A  B)
B)  C).
C).
Bijv.: {A B
B  C}
C}
 (A
(A  (B
(B  C)).
C)).
Bijv.: {(A B)
B)  C}
C}
 (A
(A  (B
(B  C)).
C)).
Bijv.: {A (B
(B  C)}
C)}
 ((A
((A  B)
B)  C).
C).
(5.3.3)  B
B  C}
C}
 ((A
((A  B)
B)  C).
C).Bijv.: {A
 B
B  C}
C}
 (A
(A  (B
(B  C)).
C)).Bijv.: {(A
 B)
B)  C}
C}
 (A
(A  (B
(B  C)).
C)).Bijv.: {A
 (B
(B  C)}
C)}
 ((A
((A  B)
B)  C).
C).In Implicatie.
Symmetrie geldt niet voor implicatie {
 } en zijn inverse variant {
} en zijn inverse variant {
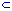 }.
}.
Bijv.: 'A  Q' : wff.
Q' : wff.
Bijv.: 'A Q
Q  x' : wff, niet
wff+.
x' : wff, niet
wff+.
Bijv.: '(A Q)
Q)  x' : wff+.
x' : wff+.
Bijv.: 'A (Q
(Q  x)' : wff+.
x)' : wff+.
 Q' : wff.
Q' : wff.Bijv.: 'A
 Q
Q  x' : wff, niet
wff+.
x' : wff, niet
wff+.Bijv.: '(A
 Q)
Q)  x' : wff+.
x' : wff+.Bijv.: 'A
 (Q
(Q  x)' : wff+.
x)' : wff+.Keten/ ketting-redenering, met geldige parafrase.
Bijv.: {A  B
B  C}
C}
 ((A
((A  B)
B)
 C).
C).
D.w.z.: 'A B
B  C'
C'
mag herschreven en/of geïnterpreteerd worden als: '(A B)
B)
 C';
C';
maar niet als: 'A (B
(B  C)'.
C)'.
 B
B  C}
C}
 ((A
((A  B)
B)
 C).
C).D.w.z.: 'A
 B
B  C'
C'mag herschreven en/of geïnterpreteerd worden als: '(A
 B)
B)
 C';
C';maar niet als: 'A
 (B
(B  C)'.
C)'.Keten/ ketting-redenering, met alleen geldige degressie.
Bijv.: {(A  B)
B)  C}
C}
 (
( (B
(B  C)). (Géén equivalentie!).
C)). (Géén equivalentie!).
(5.3.4)  B)
B)  C}
C}
 (
(degres
) (A (B
(B  C)). (Géén equivalentie!).
C)). (Géén equivalentie!).In Equivalentie.
Bijv.: {A  B
B  C}
C}
 ((A
((A  B)
B)
 C) : is
C) : is
Bijv.: {A B
B  C}
C}
 (A
(A  (B
(B  C)) : is
C)) : is
(5.3.5)  B
B  C}
C}
 ((A
((A  B)
B)
 C) : is
C) : is ongeldig
.Bijv.: {A
 B
B  C}
C}
 (A
(A  (B
(B  C)) : is
C)) : is ongeldig
.In Exclusief Disjunctie.
Bijv.: 'A
Bijv.: '{A ((A
((A
Bijv.: '{A (A
(A
(5.3.6) #
B#
C'..
: is niet toegestaan (syntactisch onwelgevormd; want semantisch onmogelijk in bivalent systeem).Bijv.: '{A
#
B#
C} ((A
((A #
B)#
C)' : is dus niet van toepassing.Bijv.: '{A
#
B#
C} (A
(A #
(B#
C))' : is dus evenmin van toepassing.In Exclusie.
Bijv.: {A | B | C}  ((A | B) | C).
((A | B) | C).
Bijv.: {A | B | C} (A | (B | C)).
(A | (B | C)).
Bijv.: {(A | B) | C} (A | (B | C)).
(A | (B | C)).
Bijv.: {A | (B | C)} ((A | B) | C).
((A | B) | C).
(5.3.7)  ((A | B) | C).
((A | B) | C).Bijv.: {A | B | C}
 (A | (B | C)).
(A | (B | C)).Bijv.: {(A | B) | C}
 (A | (B | C)).
(A | (B | C)).Bijv.: {A | (B | C)}
 ((A | B) | C).
((A | B) | C).In Parallelle Negatie.
Bijv.: {A \ B \ C}  ((A \ B) \ C).
((A \ B) \ C).
Bijv.: {A \ B \ C} (A \ (B \ C)).
(A \ (B \ C)).
Bijv.: {(A \ B) \ C} (A \ (B \ C)).
(A \ (B \ C)).
Bijv.: {A \ (B \ C)} ((A \ B) \ C).
((A \ B) \ C).
 ((A \ B) \ C).
((A \ B) \ C).Bijv.: {A \ B \ C}
 (A \ (B \ C)).
(A \ (B \ C)).Bijv.: {(A \ B) \ C}
 (A \ (B \ C)).
(A \ (B \ C)).Bijv.: {A \ (B \ C)}
 ((A \ B) \ C).
((A \ B) \ C).6.
Parafrase via Syntactische verandering: volgorde (Commutatief).
Volgorde-verandering, Commutatie.
Bijv. t.b.v. standaardisatie, via herordening volgens informele (conventioneel gangbare) alfanumerieke volgrode.
(Alfanumeriek is een verzamelnaam voor de letters van het alfabet en de cijfers 0 tot en met 9. Er zijn dus 36 alfanumerieke tekens, of 62 wanneer onderscheid wordt gemaakt tussen hoofd- en kleine letters).
(6.1)
In Conjunctie.
Bijv.: {A  B}
B}  (B
(B
 A).
A).
(6.2)  B}
B}  (B
(B
 A).
A).In Disjunctie.
Bijv.: {A  B}
B}  (B
(B
 A).
A).
(6.3)  B}
B}  (B
(B
 A).
A).In Implicatie.
Bijv.: {A  B}
B}  (B
(B
 A) : is
A) : is
Wel geldig zijn: B}
B}  (B
(B
 A) : is
A) : is ongeldig
.
(6.3a)
Connectief verandering.
C.q. Transpositie regel.
Het aaneenschakelen van redeneringen.
O.a. t.b.v. Bewijs via 'kettingredenering' of 'ketenredenering' (sorites), c.q. 'sluitredenering' ( syllogisme).
(6.4) Transformatie naar Inverse implicatie.
Connectief verandering.
Bijv.: {A  B}
B}  (B
(B
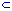 A).
A).
(6.3b)  B}
B}  (B
(B
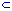 A).
A).Wet van de Contrapositie.
C.q. Transpositie regel.
Bijv.: {A  X} [
X} [
 (¬A
(¬A  X);
X);
 (X
(X  ¬A);]
¬A);]
 (¬X
(¬X  ¬A).
¬A).
(6.3c)  X} [
X} [
 (¬A
(¬A  X);
X);
 (X
(X  ¬A);]
¬A);]
 (¬X
(¬X  ¬A).
¬A).Keten/ ketting-redenering, met geldige parafrase.
Het aaneenschakelen van redeneringen.
O.a. t.b.v. Bewijs via 'kettingredenering' of 'ketenredenering' (sorites), c.q. 'sluitredenering' ( syllogisme).
(6.3c.1)
Van geneste premisse naar geneste conjunctie.
Oftewel Deductiestelling (Deduction theorem).
Van conjuncte premisse naar geneste enkevoudige premisse.
Inverse van Deductiestelling.
Een - 'Lambda-anonieme' - functie met meerdere argumenten c.q. premissen wordt omgezet in een keten van functies met enkelvoudige input die elkaar geconditioneerd c.q. genest aanroepen:
Wet van Import.
Van geneste premisse naar geneste conjunctie.
Oftewel Deductiestelling (Deduction theorem).
Bijv.: {(A  (B
(B  C ) };
C ) };
 ((A
((A  B)
B)
 C ).
C ).
Dus ook: {A (B
(B  C)}
C)}
 ((B
((B  A)
A)
 C).
C).
Idem, algemener:
Bijv.: {A[i] (A[2]
(A[2]
 ( .. (A[n]
( .. (A[n]  C) .. )) }
C) .. )) }
 (A[1]
(A[1]  (A[2]
(A[2]
 ((A[3], .. A[n])
((A[3], .. A[n])  C)) );
C)) );
 (A[1]
(A[1]  ((A[2]
, .. A[n])
((A[2]
, .. A[n])  C) );
C) );
 ((A[1], .. A[n])
((A[1], .. A[n])
 C ).
C ).
Idem, compacter:
Bijv.: { (i
(i  (1..n))} {A[i]
(1..n))} {A[i]
 ((A[1], .. A[i-1], A[i+1], .. A[n]
)
((A[1], .. A[i-1], A[i+1], .. A[n]
)  C ) ) }
C ) ) }  ((A[1]
, .. A[n])
((A[1]
, .. A[n])  C).
C).
Idem, voor verzamelingen:
Bijv.: { K* = {A[1], .. A[n]}
K* = {A[1], .. A[n]}
 (K*
(K*  (B
(B
 C));
C));  ({K*
({K*
 B}
B}  C).
C).
(6.3c.2)  (B
(B  C ) };
C ) };
[ (¬A
(¬A  (¬B
(¬B
 C ) );
C ) );  (¬A
(¬A
 ¬B
¬B  C );
C );
 ((¬A
((¬A  ¬B)
¬B)
 C );
C );  (¬(A
(¬(A
 B)
B)  C );]
C );]
 (¬A
(¬A  (¬B
(¬B
 C ) );
C ) );  (¬A
(¬A
 ¬B
¬B  C );
C );
 ((¬A
((¬A  ¬B)
¬B)
 C );
C );  (¬(A
(¬(A
 B)
B)  C );]
C );] ((A
((A  B)
B)
 C ).
C ).Dus ook: {A
 (B
(B  C)}
C)}
 ((B
((B  A)
A)
 C).
C).Idem, algemener:
Bijv.: {A[i]
 (A[2]
(A[2]
 ( .. (A[n]
( .. (A[n]  C) .. )) }
C) .. )) } (A[1]
(A[1]  (A[2]
(A[2]
 ((A[3], .. A[n])
((A[3], .. A[n])  C)) );
C)) ); (A[1]
(A[1]  ((A[2]
, .. A[n])
((A[2]
, .. A[n])  C) );
C) ); ((A[1], .. A[n])
((A[1], .. A[n])
 C ).
C ).Idem, compacter:
Bijv.: {
 (i
(i  (1..n))} {A[i]
(1..n))} {A[i]
 ((A[1], .. A[i-1], A[i+1], .. A[n]
)
((A[1], .. A[i-1], A[i+1], .. A[n]
)  C ) ) }
C ) ) }  ((A[1]
, .. A[n])
((A[1]
, .. A[n])  C).
C).Idem, voor verzamelingen:
Bijv.: {
 K* = {A[1], .. A[n]}
K* = {A[1], .. A[n]}
 (K*
(K*  (B
(B
 C));
C));  ({K*
({K*
 B}
B}  C).
C).Wet van Export.
Van conjuncte premisse naar geneste enkevoudige premisse.
Inverse van Deductiestelling.
Idem, algemener:
Bijv.: {(A[1], C}
C}
 (A[1]
(A[1]  ((A
[2],
((A
[2],  C) );
C) );
 (A[1]
(A[1]  (A
[2]
(A
[2]  ((A[3],
((A[3],  C)) );
C)) );
 (A[i]
(A[i]  (A
[2]
(A
[2]  (
(  C)
C)
Idem, compacter:
Bijv.: {((A[1], C)
C)
 (i IN (1..n))}
(i IN (1..n))}  (A[i]
(A[i]
 ((A[1],
((A[1],  C))).
C))).
Idem, voor verzamelingen:
Bijv.: { K* = {A[1], .. A[n]}
K* = {A[1], .. A[n]}
 {(K*
{(K*  B)
B)
 C}
C}  (K*
(K*
 (B
(B  C)).
C)).
Bijv.: {(A[1],
..
A[n]) C}
C} (A[1]
(A[1]  ((A
[2],
((A
[2], ..
A[n]) C) );
C) ); (A[1]
(A[1]  (A
[2]
(A
[2]  ((A[3],
((A[3], ..
A[n]) C)) );
C)) );..
 (A[i]
(A[i]  (A
[2]
(A
[2]  (
( ..
(A[n] C)
C) ..
)) ).Idem, compacter:
Bijv.: {((A[1],
..
A[n]) C)
C)
 (i IN (1..n))}
(i IN (1..n))}  (A[i]
(A[i]
 ((A[1],
((A[1], ..
A[i-1], A[i+1] ,..
A[n]) C))).
C))).Idem, voor verzamelingen:
Bijv.: {
 K* = {A[1], .. A[n]}
K* = {A[1], .. A[n]}
 {(K*
{(K*  B)
B)
 C}
C}  (K*
(K*
 (B
(B  C)).
C)).Currying in Lambda-calculus.
Een - 'Lambda-anonieme' - functie met meerdere argumenten c.q. premissen wordt omgezet in een keten van functies met enkelvoudige input die elkaar geconditioneerd c.q. genest aanroepen:
Bijv. {(a,b)  (x *y)} wordt: {a
(x *y)} wordt: {a
 (b
(b  (x *y))}.
(x *y))}.
Idem, algemener:
Bijv.: {(a[1], C}
C}
 (a[1]
(a[1]  (a
[2]
(a
[2]  (
(  C)
C)
Daarvan afgeleid: (x *y)} wordt: {a
(x *y)} wordt: {a
 (b
(b  (x *y))}.
(x *y))}.Idem, algemener:
Bijv.: {(a[1],
..
a[n]) C}
C} (a[1]
(a[1]  (a
[2]
(a
[2]  (
( ..
(a[n] C)
C) ..
)) ).Wet van de Commutativiteit.
Bijv.: {A  (B
(B  C)}
C)}
 (B
(B  (A
(A
 C)).
C)).
 (B
(B  C)}
C)}
[ (¬A
(¬A  (¬B
(¬B
 C));
C));  (¬A
(¬A
 ¬B
¬B  C);
C);
 (¬B
(¬B  ¬A
¬A
 C);
C);  (¬B
(¬B
 (¬A
(¬A  C));]
C));]
 (¬A
(¬A  (¬B
(¬B
 C));
C));  (¬A
(¬A
 ¬B
¬B  C);
C);
 (¬B
(¬B  ¬A
¬A
 C);
C);  (¬B
(¬B
 (¬A
(¬A  C));]
C));] (B
(B  (A
(A
 C)).
C)).In Equivalentie.
Bijv.: {A  B}
B}  (B
(B
 A).
A).
(6.5)  B}
B}  (B
(B
 A).
A).In Exclusief Disjunctie.
Bijv.: {A  (B
(B
(6.6) #
B} (B
(B #
A).In Exclusie.
Bijv.: {A | B}  (B | A).
(B | A).
(6.7)  (B | A).
(B | A).In Parallelle Negatie.
Bijv.: {A \ B}  (B \ A).
(B \ A).
 (B \ A).
(B \ A).C.P. van der Velde © 2004, 2015, 2018.