Course / training:
Method for Logical Analysis
Principles of Formal logic.
Combinatory Explosion in Logical Systems
Contents
1. Introduction: Information, logic and complexity.
1.a. Foundations of a Logical system
1.b. Starting parameters
2. Semantic expansion.
1.a. Foundations of a Logical system
1.b. Starting parameters
2. Semantic expansion.
2.1. Elementary object states.
2.2. Domain states.
2.3. Logical relations.
2.4. Truth values table.
2.5. Arguments (Semantic).
2.6. Inference schemes (Syntactic).
2.7. Inferences, derivations (Semantic).
2.8. Valid reasonings.
2.9. Table of dimensions.
2.10. Numbers for comparision.
2.2. Domain states.
2.3. Logical relations.
2.4. Truth values table.
2.5. Arguments (Semantic).
2.6. Inference schemes (Syntactic).
2.7. Inferences, derivations (Semantic).
2.8. Valid reasonings.
2.9. Table of dimensions.
2.10. Numbers for comparision.
Combinatory Explosion in Logical Systems
1.
Introduction:
the emergence of a System of Logic.
Judgment makes use of information.
Our judgments and estimations are in many ways like our other reactions and decisions.
They are based on information we have available - at conscious as well as subconscious levels.
Information and difference.
About the concept of 'information' a lot of different views and understands exist. To avoid misunderstandings, and grasp its essential meaning, it's useful to first look at its most characteristic property. This becomes apparant when we try to conceive of a situation where she is totally absent.
Clearly, without any information there is only utter chaos, senseless 'noise', total vagueness, a completely non-knowing.
Information only comes into play with the perception of any difference. As soon as a distinction can be made - eg a difference between on/off, in/out, true/false, etc. - some order emerges. Only then reasoning becomes possible, and logic applies. Every amount of information thus implies at least one difference.
Information and ordering.
Any difference on its turn implies at least two 'things', phenomena or states in an area in reality. Thus, based on distinctions, combinations of things can be be considered.
Between these things simultaneously exists at least one order, ie the one that necessarily follows from their difference as perceived.
Moreover, in order to make any sense to us, information in general can not purely consist of loose data. We view the information in a certain cohesion. This implies that it allows for some ordering to be distinguished.
Viewed in reverse, every ordered state, or structure, represents in itself a certain amount of information.
Logical relations.
Given a random collection of elements, we may take a look at the logical relations that are possible between those elements. The logical relations refer to the range of states or values which the elements can take seperately, as well as through their mutual derivation relations.
Information and reasoning.
By combining data, we may obtain more complex forms of information.
Naturally, we do this by means of our thinking.
Every train of thought, and in fact every process of information processing, has the general form of a reasoning, that is to say:
Reasoning:
A number of input data are combined, and next certain data are derived from the combination.
The ways in which those combinations can be made, and the values that these combinations can take, are determined by the laws of
logic.A number of input data are combined, and next certain data are derived from the combination.
Of course these properties certainly apply to judgments and estimations. They are to be considered as reasonings, in that they operate on certain information, and produce information thereafter.
Laws of logic.
The logical laws only apply to the relations between data, ie the combinations and derivations, and not to the individual data (such as direct observations and feelings). They also apply independently of the content and the nature of the data, which includes possible variations in subject, domain, problem, purpose, application, scope, etc..
Levels of logical complexity.
Each form of reasoning, or argument, consists of a combination of one or more distinct logical relations.
Orderings, and therefore arguments, are possible in every imaginable form, but also in every unthinkable form: they are virtually unlimited in possible variation, complexity and size. As will be show below, in a few steps this already reaches far beyond the limits of the imagination and comprehension of people, and even beyond the capacities of calculation and data storage of physical and even theoretical computers of any conceivable size.
Fortunenately, all of these possible forms can be sorted out en judged with help of the laws of logic. Therefore, understanding the laws of logic is indispensable for every judgment being meaningful and reliable. For the optimal use of logic, a clear understanding of the minimal levels of logical complexity and their proportions is indispensable.
1.a.
Foundations of a Logical system.
In this overview we look at the logical possibilities that follow from an arbitrary collection units (items or objects ). We'll see in what ways combinatorial explosion occurs, to what extent this happens and what consequences it has for the complexity of information processing and judgment regarding the input data.
To limit ourselves to the most generally valid principles we will focus on a logical system which itself is of minimal complexity . From this system, propositionlogic can be derived, but also, with the necessary additions, more complex systems such as predicate logic and modal logic.
In general applies that the consequences of combinatorial explosion and complexity themselves increase in explosive ways with each degree of increasing refinement of the logical system which we apply.
Logical system at semantic level.
S!
: a logical system ('apparatus', calculus).S!
PPL :S!
is a system in propositional logic (PPL
) (or higher).S!
PDL-I :S!
is a system in predicate logic (PDL-I
), first-order logic (FOL
) (or higher).S!
) : the semantics, a set of ordering rules, ofS!
.Logical system at syntactical level.
L!
: a formal system (language system).L!
PPL :L!
is a language/system in propositional logic (or higher).L!
PDL-I :L!
is a language/system in predicate logic, first-order logic ,FOL
, (or higher).L!
) : the syntaxis, or grammer, a set of ordering rules, ofL!
.WFF*(
L!
)) : the set of well-formed statements (formulas) ofL!
.1.b.
Starting parameters.
1.1.
Objects.
Applicable in
PPL
and further.D
* : (referential) domain or population, set of elements d[i]; with (i=
1,..
d).d : domain- or population-size; total number of objects, domain-elements ('things', phenomena , items, variables) d[i] within
D
*.D
*=
{d[1], .. d[i], .. d[d] }.d
=
|
D
*|
.Example.
With two items (d
=
2 ), the setD
·d may consist of the following elements (objects), represented by proposition symbols and stated in arbitrary order:
{ (d =
2 )(D
·d=
{' A' ,' B'} ) }.S!
[s1] however extremely minimal, if not futile.Some examples of statements in such a 'minimal' system, stated in a formal language:
{ (d (
Likewise, the domain may consist of only one element. But then the inference systems =
0 )(D
·d=
{} ) : ({}=
(v) {} ); (({})$
=
(v)$
0 ); ({}=
(r)$
0 ); etc.}.S!
[s1 ] also remains very simple.Some examples of statements in such a 'primitive' system, stated in a formal language:
{ (d (
=
1 )(D
*=
{d [1]} ) : ((d[1] )$
=
(v)$
1 ); ((d[1] )$
=
(v)$
0 ); etc.}.Range.
When the number of objects is less then one, any reasoning becomes meaningless.
On the other hand, when it is infinite, an inconceivable amount of reasoning concerning the domain becomes practically undecidable.
For a domain which is manageable, the following applies:
{ (d (1 
0 ) }.
=
|
D
*(mgb
)|
);(1 ≤
d<
0 ) }.1.2.
Values.
Generally applicative to objects.
V
* : value system or 'value palette', set of values v[j]; waarbij (j=
1,..
v).v : total number of values, state values, object values or signal values (valences ); e.g. truth values, v[j] in
V
*.V
*=
{v[1], .. v[j], .. v[v] }.v
=
|
V
*|
.Example.
With two values (v
=
2 ) the setV
·v may consist of the following elements (values), represented by value constants and stated in arbitrary order:{ (v =
2 )(V
·v=
{0 ,1 } ) }.Range.
When the number of values is less then two, any assignment of value becomes meaningless, and thus any attempt to meaningful reasoning becomes impossible.
On the other hand, when this number is infinite, almost any reasoning concerning the domain becomes practically undecidable.
For a value set which is sensible and manageable, the following applies:
{ (v (2
0 ) }.
=
|
V
*(mgb
)|
);(2 ≤
v<
0 ) }.1.3.
Parameters for Predicate logic.
In
PDL
some further parameters come into play.
(2a) p : total number of predicate-variables (attributes, predicate names); including identity, '='.
(2b) r(v,d) : (maximum) number of argument-places, or arity, for each predicate name.
(We may eventually use for simplicity and security the maximum over all predicate names).
(2c) n : total number of elements (individuals, objects) in the referential domain (the population).
The (maximum) number of items a in (2b) r(v,d) : (maximum) number of argument-places, or arity, for each predicate name.
(We may eventually use for simplicity and security the maximum over all predicate names).
(2c) n : total number of elements (individuals, objects) in the referential domain (the population).
PDL
is a derivate of the latter three.{p ≤
a≤
(p *MAX(1,(r (v,d)*
n)) }.PDL
system we have sufficient information about the parameters p, r (v,d) and n, we can calculate a, and may reason further following the rules for aPPL
system.Below we explore which combinatorial possibilities are generated by these parameters on the semantic level and the syntactic level respectively.
2.
Semantic expansion .
2.1.
Elementary object states .
Object states constitute pairs or tupels (the Cartesisch product) from the v values and d elements.
They reflect the domain at an observational level.
At a semantical level these are truth statements with respect to separate objects.
In logical language these are e.g. literals, ground instances, or 'witnesses'.
They resemble samples from a population.
H
·(v,d) : The set of all possible unique object states.Example.
With two truth values (v
=
2, binary system) and two items (d=
2) the setH
·(v,d) may consist of the following elements (object states), represented by proposition symbols and stated in arbitrary order:(H
·(v=
2,d=
2)=
{' A' ,'¬A' ,' B' ,'¬B' } ).Size.
h(v,d) : The total number of possible unique object states.
{ 
v d
( h(v,d) :=
|
H
·(v,d)|
;:=
(|
V
·v|
,|
D
·d|
;:=
v*
d )d, v }.In a binary system.
Under (v
=
2 ) applies:H
·(v,d) is just as large as the doubling of setD
·d.The values h(2,d) largely correspond to the sequence A005843 (formerly M0985) in the On-line Encyclopedia of Integer Sequences (OEIS).
{ d ( h(2,d) :=
2*
d;:=
A005843(d )|
(offset 0 ) )d }.
Eg., from (d
follows (h(2,d)
=
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..
} );follows (h(2,d)
=
{ 2, 4, 6, 8, 10, 12, 14, 16, 18, 20,..
}.Range.
The number h(v,d) remains liniar (polynomial) in d.
(2 ≤
h(v,d)<
0 ).Complexity class.
The set
H
·(v,d) remains within the class of countable infinite sets (denumerable sets).Thus it can be searched algorithmically (it is tracktable) - with a singletape Turing machine - in linear polynomial computational time (
P-TIME
).(H
·(v,d)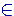
POLY
(d^1 );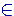TIME
(d );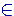
P-TIME
).2.2.
Domain states.
Domain states consist of conjunct combinations of all objects with their specific values, ie various object states.
They reflect the domain in a purely descriptive way.
At a semantical level these are truth statements with respect to the state of the entire domain.
They are similar to the cells (categories of variance) in a so-called contingency table (cross tabulation , of 'crosstab'), which forms the basis of numerous statistical measures for the comparision of variances, in particular Chi-square (Χ2), and variants or derivates of the latter, such as correlation coefficient, regression coefficient, Student's t, F, Fisher z, etc..
B
·(v,d) : The set of all possible unique domain states.Example.
With two truth values (v
=
2, binary system) and two items (d=
2) the setB
·(v,d) may consist of the following elements (domain states), represented by proposition symbols and stated in arbitrary order:(B
·(v=
2,d=
2)=
{'( A
B)' ,'( A
¬B)' ,'(¬A B)' ,'(¬A ¬
B)' } ).Size.
b(v,d) : The total number of possible unique domain states.
The number b(v,d) equals the number of repetition variantions, or, sequence variations with replacement i.e. repetition, with size (length) d from v elements.
{ v d
( b(v,d) :=
|
B
·(v,d)|
;:=
(d1 := 1, ..
d ) v;=
v ^d;:=
b(v,d -1 )*
v )d, v }.It is equal to the number of rows in the truth-values table.
In a binary system.
Under (v
=
2 ) applies:B
·(v,d) is just as large as the set of all possible subsets - the power set - ofD
·d.In a binary system the number of domain states represents the quantity of signal, signal content, or signal capacity , which is measured as the amount of domain elements d in bits (binary digits):
The values b(2,d) correspond to the sequence A000079 (formerly M1129, N0432) in the OEIS.
I.e.:
{ d ( b(2,d) :=
|
P
·d|
;:=
b (2,d -1 )*
2;:=
lg2 d bits;:=
A000079(d )|
(offset 0 ) )d }.
Eg., from (d
follows (b(2,d)
=
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..
} );follows (b(2,d)
=
{ 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024,..
} ).Range.
The number b(v,d) remains exponential in d.
(2 ≤
b(v,d)<
0 ^0 );
Complexity class.
The set
B
·(v,d) remains within the class of uncountable infinite sets , which have the size of the continuum (cardinality of the continuum).Thus it can only be searched algorthmically in exponential computational time (
EXP-TIME
).(B
·(v,d)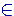
EXP-TIME
(d ) ).2.3.
Logical relations.
Logical relations reflect the domain at an analytical level.
At a semantical level they constitute the possible conditional truth statements with respect to the entire domain or parts of it.
In logical languages these are e.g. truth-value patterns, formulas, propositions, theorems, and the like.
They correspond to the columns in the truth-values table.
T
·(v,d) : The set of all possible unique logical relations.Example.
With two truth values (v
=
2, binary system) and two items (d=
2), the setT
·(v,d) may consist of the following elements (logical relations), represented by proposition symbols and stated in arbitrary order:T
·(v=
2,d=
2)=
{' T' ,' F'
,' A' ,' B' ,'¬A' ,'¬B'
,'( A B)' ,'( A ¬B)' ,'(¬
A B)' ,'(¬A ¬B)'
,'( A
B)' ,'( A ¬B)' ,'(¬
A B)' ,'(¬A ¬B)'
,'( A
B)' ,'( A
,' A' ,' B' ,'¬A' ,'¬B'
,'( A
B)' ,'( A ¬B)' ,'(¬
A B)' ,'(¬A ¬B)','( A
B)' ,'( A ¬B)' ,'(¬
A B)' ,'(¬A ¬B)','( A
B)' ,'( A #
B)' } ).Size.
t(v,d) : The total number of possible unique logical relations.
The number t(v,d) equals the numer of order variations or permutations with repetition with size (length) b(v,d) from v elements.
{ v d
( t(v,d) :=
|
T
·(v,d)|
);:=
(b1 := 1, ..
b(v, d) ) v;:=
|
B
·(v,b( v,d))|
;:=
v ^|
B
·(v,d)|
;:=
v ^b(v,d );:=
v ^(v ^d);:=
t(v,d -1 )*
v ) d, v }.In a binary system.
Under (v
=
2 ) applies:T
·(v,d) is just as large as the power set of the power set ofD
·d.The values t(2,d) correspond to the sequence A001146 (formerly M1297, N0497) in the OEIS.
{ d ( t(2,d) :=
|
P
·b(2,d)|
;:=
|
P
·|P
·d|
|
);:=
t(2,d -1 )*
2;:=
A001146(d )|
(offset 0 ) )d }.
Eg., { t(2, 1)
t(2, 2)
t(2, 3)
t(2, 4)
t(2, 5)
t(2, 6)
t(2, 7)
t(2, 8)
t(2, 9)
t(2, 10)
=
4,t(2, 2)
=
16,t(2, 3)
=
256,t(2, 4)
=
65536,t(2, 5)
=
4.294967 296 ·(10^ 9),t(2, 6)
=
1.844674 407370 955161 6 ·(10^ 19),t(2, 7)
=
3.402823 669209 384634 633746 074317 682114 56 ·(10^ 38),t(2, 8)
=
1.157920 892373 161954 235709 850086 879078 5326 ·(10^ 77),t(2, 9)
=
1.340780 792994 259709 957402 499820 584612 7479 ·(10^ 154),t(2, 10)
=
1.797693 134862 315907 729305 190789 024733 6179 ·(10^ 308),..
}.Range.
The number t(v,d) remains hyper-exponential in d.
(2 ≤
t(v,d)<
0 ^(0 ^
0 ) );
Complexity class.
The set
T
·(v,d) can be searched in hyper-exponential computational time (2-EXP-TIME
).(T
·(v,d)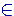
2-EXP-TIME
(d ) ).2.4.
The Truth-values table.
Given a domain
D
·d and value setV
·v, the possible immediate logical relations-between-relations are completely defined through the so-called truth-values table .This is construed on basis of systematic value assignment (validation) of the objects by a simple standarized algorithm. The objects each in turn go through the range of values, through so-called 'nested' cycles (loops), thus getting their unique, ordered truth-value patterns. Next, all other ordered value combinations are filled in. In this way a closed, coherent table arises of all possible sequences of (truth) values given parameters (d,v).
The value patterns are simular to statements with at least one proverb, or clause, in other words, 'sentences'.
In a binary system, they are expressed by binary numbers. Each of them has length of b(v,d) value constants . These are simular to characters or symbols in written language.
The length b(v,d) equals the amount of information in standard units: bits.
Furthermore, the table represents, with perfect garantees, all possible elementary logical relations together with their definite, immediate mutual logical relations.
W
·(v,d)[T
] : The ordered set of all cells in the truth-values table.Example.
Truth value table for a logical system with (v =2) values and (d=2) variables, interpreted for proposition logic (
PPL
), predicate logic (PDL
), and shorthand Skolem form (Sk
) respectively.
Table bivalid value combinations |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Value pattern |
Logical relation in PPL |
Logical relation in PDL |
Logical relation in Skolem L. |
Logical power | ||||||
| 1 | 1 | 1 | 1 | 1 |
T |
¬F |
X ¬X |
0 | |||
| 2 | 0 | 0 | 0 | 0 |
F |
¬T |
X ¬X |
1 | |||
| 3 | 1 | 1 | 0 | 0 |
A1 |
¬¬A1 |
0.50 | ||||
| 4 | 1 | 0 | 1 | 0 |
A2 |
¬¬A2 |
0.50 | ||||
| 5 | 0 | 0 | 1 | 1 |
¬A1 |
¬A1 |
0.50 | ||||
| 6 | 0 | 1 | 0 | 1 |
¬A2 |
¬A2 |
0.50 | ||||
| 7 | 1 | 0 | 0 | 0 |
A1 A2 |
¬(¬A1 ¬A2) |
x A[x] |
¬ x ¬A[x] |
A[x] |
0.75 | |
| 8 | 0 | 1 | 0 | 0 |
A1 ¬A2 |
¬(¬A1 A2) |
0.75 | ||||
| 9 | 0 | 0 | 1 | 0 |
¬A1 A2 |
¬(A1 ¬A2) |
0.75 | ||||
| 10 | 0 | 0 | 0 | 1 |
¬A1 ¬A2 |
¬(A1 A2) |
A1\A2 |
¬x A[x] |
x ¬A[x] |
¬A[x] |
0.75 |
| 11 | 1 | 1 | 1 | 0 |
A1 A2 |
¬(¬A1 ¬A2) |
x A[x] |
¬x ¬A[x] |
A[cs] |
0.25 | |
| 12 | 1 | 1 | 0 | 1 |
A1 ¬A2 |
¬(¬A1 A2) |
A1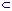 A2 |
0.25 | |||
| 13 | 1 | 0 | 1 | 1 |
¬A1 A2 |
¬(A1 ¬A2) |
A1 A2 |
0.25 | |||
| 14 | 0 | 1 | 1 | 1 |
¬A1 ¬A2 |
¬(A1 A2) |
A1|A2 |
¬x A[x] |
x ¬A[x] |
¬A[cs] |
0.25 |
| 15 | 1 | 0 | 0 | 1 |
A1 A2 |
¬(A1#A2) |
(A1 A2)
(¬A1 ¬A2) |
0.50 | |||
| 16 | 0 | 1 | 1 | 0 |
A1#A2 |
¬(A1 A2) |
(A1 ¬A2)
(¬A1 A2) | 0.50 | |||
Size.
w(v,d)t : The total number of cells in the truth-values table.
The number w(v,d)t(v,d) becomes the product of the number of domain states (rows) b(v,d), and the number of domain-state relations (columns) t(v,d ):
{ v d
( w(v,d)t :=
|
W
·( 2,d)t|
;:=
|
(T
*(v,d ),B
*(v,d) )|
;:=
(|
T
*(v,d)|
*
|
B
*(v,d)|
);:=
(|
B
*(v,b(v,d))|
*
|
B
*(v,d)|
);:=
b(v,d)*
t(v,d);:=
v ^(v ^d )*
v ^d;:=
v ^((v ^d) +d ) ) d, v }.In a binary system.
Under (v
=
2 ) applies:{ d ( w(2,d)t
:=
|
W
·(2,d)t|
;:=
2 ^((2 ^d) +d ) )d }.
E.g., { w(2, 1)t
w(2, 2)t
w(2, 3)t
w(2, 4)t
w(2, 5)t
w(2, 6)t
w(2, 7)t
w(2, 8)t
w(2, 9)t
w(2,10)t
=
8,w(2, 2)t
=
64,w(2, 3)t
=
2018,w(2, 4)t
=
1.048576 ·(10^6),w(2, 5)t
=
1.37438953472 ·(10^11),w(2, 6)t
=
1.180591620717411303424 ·(10^21 ),w(2, 7)t
=
4.3556142965880123323311949751266331066368 ·(10^40 ),w(2, 8)t
=
2.9642774844752946028434172162224104410437 ·(10^79 ),w(2, 9)t
=
6.8647976601306097149819007990813932172694 ·(10^156 ),w(2,10)t
=
1.8408377700990114895148085153679613272248 ·(10^311 ),..
}.The same sequence in bytes (8-bits):
{ 1,
8,
256,
1.31072 ·(10^5,
1.717986 9184 ·(10^10,
1.475739 525896 764129 28 ·(10^20,
5.444517 870735 015415 413993 718908 291383 2960 ·(10^39,
3.705346 855594 118253 554271 520278 013051 3046 ·(10^78,
8.580997 075163 262143 727375 998851 741521 5868 ·(10^155,
2.301047 212623 764361 893510 644209 951659 0310 ·(10^310,
8,
256,
1.31072 ·(10^5,
1.717986 9184 ·(10^10,
1.475739 525896 764129 28 ·(10^20,
5.444517 870735 015415 413993 718908 291383 2960 ·(10^39,
3.705346 855594 118253 554271 520278 013051 3046 ·(10^78,
8.580997 075163 262143 727375 998851 741521 5868 ·(10^155,
2.301047 212623 764361 893510 644209 951659 0310 ·(10^310,
..
}.2.5.
Arguments (Semantic).
In setting up an argument we usually don't make use of all possible logical relations about the subject in question, but a certain selection, or subset, of
T
·(v,d).Arguments constitute of unique combinations of logical relations (i.e. without doubles).
At a semantic level these are sets of conditional truth-value statements which we regard in conjunction.
They reflect the domain at a discursive level.
In logical languages these are sets of truth-value patterns, formulas, propositions, theoremes, and the like: so called ' theories'.
For a solid analysis we have to take all possible selections into account.
U
·(v,d) : The set of all possible unique arguments.Example.
In an extremely simple, so to say 'primitive' logical system, with two truth values (v
=
2, binary system ) and only one item (d=
1), the setU
·(v,d) may consist of the following subsets (arguments), represented here as combinations of logical relations stated in terms of propositiesymbols , and in arbitrary order:U
·(v=
2,d=
1)=
{ {}
,{' T'}
,{' T' ,' F'} {' T' ,' A'} {' T' ,'¬A'}
,{' T' ,' F' ,' A'} ,{' T' ,'F' ,'¬A'} ,{' T' ,' A' ,'¬A'}
,{' T' ,' F' ,' A' ,'¬A'}
,{' F'}
,{' F' ,' A'} ,{' F' ,'¬A'}
,{' F' ,' A' ,'¬A'}
,{' A'}
,{' A' ,'¬A'}
,{¬A'} }.
,{' T'}
,{' T' ,' F'} {' T' ,' A'} {' T' ,'¬A'}
,{' T' ,' F' ,' A'} ,{' T' ,'F' ,'¬A'} ,{' T' ,' A' ,'¬A'}
,{' T' ,' F' ,' A' ,'¬A'}
,{' F'}
,{' F' ,' A'} ,{' F' ,'¬A'}
,{' F' ,' A' ,'¬A'}
,{' A'}
,{' A' ,'¬A'}
,{¬A'} }.
Size.
u(2,d) : The total number of possible unique arguments.
The number u(2,d) equals the sum of all possible unique unsorted selections (without internal repetition ) from
T
·(v,d) - i.e. of the binomial coefficients of t( v,d) above the length (number of logical relations) t1 of each subset ofU
· v,d.{ v d
( u(2,d)(v,d) :=
|
U
·(v, d)|
; ( u1 ( (U
*[ u1]
U
·(v,d) )
( (u(2,d)(v,d)[u1] :=
|
U
*[u1]|
) ( t1 ( (t1 =
u (2,d)(v,d)[u1] ) ( (U
* [u1]U
·t1 )
( U
·t1U
·(v ,d) ) ) )t1 ) ) )u1 ); ( u(2,d)(v,d)
:=
(u1 := 1, ..
u(2,d )(v,d) ) u(2,d)(v,d)[u1];:=
(t1 := 1, ..
t(v, d) ) (|
U·t1|
);:=
(t1 := 1, ..
t(v, d) )binomial
(t(v,d), t1 );:=
|
T
·(v,t(v,d))|
;:=
2 ^|
T
·(v,d)|
;:=
2 ^(v ^(v ^d)) ) )d, v }.In a binary system.
Under (v
=
2 ) applies:U
·(v,d) is just as large as the power set of the power set of the power set ofD
·d.Some of the values u(2,d)·(2,d) correspond to numbers in the sequence A051285 of the OEIS.
{ d ( u(2,d)
Eg., u(2, 1)
u(2, 2)
u(2, 3)
u(2, 4)
u(2, 5)
u(2, 6)
u(2, 7)
u(2, 8)
u(2, 9)
u(2, 10)
=
16,u(2, 2)
=
65536,u(2, 3)
=
1.157920 892373 161954 235709 850086 879078 5327 ·(10^ 77),u(2, 4)
=
2.003529 930406 846464 979072 351560 255750 4478 ·(10^ 1.9728 ·(10 ^ 4) ),u(2, 5)
=
3.103280 543863 286140 299891 155863 640203 1970 ·(10^ 1.292913 986 ·(10 ^ 9) ),u(2, 6)
=
1.906974 011604 473384 552241 746745 187983 8889 ·(10^ 5.553023 288523 357132 ·(10 ^ 18) ),u(2, 7)
=
5.404596 770346 448769 045335 584018 890286 8344 ·(10^ 1.024351 994387 393637 500121 092501 032327 0013 ·(10 ^ 58) ),u(2, 8)
=
3.792584 931520 968368 388666 761840 860509 4478 ·(10^ 3.485689 212103 261792 986571 570093 041799 6503 ·(10 ^ 76) ),u(2, 9)
=
1.536561 964731 566339 928128 482575 903914 8145 ·(10^ 4.036152 363014 112689 691315 198542 699515 0356 ·(10 ^ 153) ),u(2, 10)
=
2.371036 276223 981569 086193 449295 336389 1223 ·(10^ 5.411595 565927 717197 055868 235175 883435 8915 ·(10 ^ 307) ),..
.Range.
The number u(2,d) remains ultra-exponential in d.
(2 ≤
u(2,d)<
2 ^(
0 ^(0 ^
0 ) ) );
Complexity class.
The set
U
·(v,d) can be searched in ultra-exponential computational time (3-EXP-TIME
).(U
·(v,d)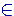
3-EXP-TIME
(d ) ).2.6.
Inference schemes, derivations, (semantic).
A very general mode of reasoning which occurs 'in nature' is the one in which at least one thinking step is taken. Typically, there is a difference between the thought content before the thought step, and that after it. In addition, the general assumption is that the second content contains an adaptation or addition to the first.
(1)
This means that from a certain collection of data (facts, connections) another set of data is derived.
Such a derivation has as its main connective the implication.
Briefly, every reasoning has the form 'premise implies conclusion'.
This means that both the premise group as the conclusion group consists of a certain subset of
Broadly speaking, this takes the form:
{ v d
k1 k2 ( ( 
Eg. (PPL):
(2)
{ v d
( 
(k1 := 1, (
k2 := 1,
This means that the set of all possible unique forms of reasoning under the parameters {
v,d} is formed by a matrix:
{ v d
(
r(v,d)U: The total number of possible unique inferences or conclusions at the semantic level.
The size of the collection is of course formed by the Cartesian product (
u(2,d) ·u(2,d)).
{ v d
( r(v,d)U
{ d ( r(2,d)U
The set
Reasoning as derivation.
This means that from a certain collection of data (facts, connections) another set of data is derived.
Such a derivation has as its main connective the implication.
Briefly, every reasoning has the form 'premise implies conclusion'.
Eg.: (X Y ).
Y ).
NB. Aristotle formulated a principle for the reasoning form called the syllogism, that is in fact valid for each form of argument:
"The syllogism is a discourse in which, certain things being laid down, another thing follows necessarily, simply because those things are laid down.
" (Aristotle, Prior Anal., 1, 1).
An argument in a system with a scale of v values about a domain with d objects will therefore have the form of
a derivation with the form:
Eg.: (X·(v,d) Y·(v,
d) ).
In general, we reason from a set of premises (premises) to a collection of conclusions.Y·(v,
d) ).This means that both the premise group as the conclusion group consists of a certain subset of
U
·(v,d).
(a) The premise is shaped by a certain subset from
(b) The conclusion is shaped by some (different or the same) subset say
U
·(v,d), sayU
·(v,d)[k1] with length (size) l[k1] elements.(b) The conclusion is shaped by some (different or the same) subset say
U
·(v,d) [k2] with length (size) l[k2] elements.R
·(v,d)[k1,k2]: reasoning from (an element of)U
·(v,d) to (an element of)U
·(v,d) .Broadly speaking, this takes the form:
{ v d
k1 k2 ( R
·( v,d)[k1,k2] ( U
·( v,d)[k1]U
·(v, d)[k2] ) )k2, k1, d, v }.
{ v1 d1 ( v1
k1 k2
( (
(
(
( ¬C ) };
( B ), (C ¬D
) } );
¬C ) )
(¬A B ), (C ¬D ) ) )
k2, k1 )d1, v1 }.
v1 d1 ( v1 =
2; d1=
4;D
·d1=
{A, B, C , D };k1 k2
( (U
·(v1,d1)[k1]U
·(v1,d1) );(U
·(v1,d1)[k2]
U
·(v1,d1) );(U
·(v1,d1)[k1]
U
·(v1,d1)[k2] );(U
·(v1,d1)[k1]=
{A, (B ¬C ) };(U
·(v1,d1)[k2]=
{¬A B ), (C ¬D
) } );R
·(v,d)[k1,k2]:=
((A, (B ¬C ) )
(¬A B ), (C ¬D ) ) )
k2, k1 )d1, v1 }.(2)
The set van derivations.
R
·(v,d)[U
]: the set of all possible unique inferences or conclusions at the semantic level. { v d
( R
·(v,d)[U
]:=
(k1 := 1, ..
u(v,d) ) (
k2 := 1, ..
u(v,d) )R
·(v,d) [U
][k1,k2] k2, k1 )d , v }.This means that the set of all possible unique forms of reasoning under the parameters {
v,d} is formed by a matrix: { v d
( R
·(v,d)[U
]:=
(U
·(v,d)X
U
·(v,d) ) ) d, v }.Size.
r(v,d)U: The total number of possible unique inferences or conclusions at the semantic level.
The size of the collection is of course formed by the Cartesian product (
u(2,d) ·u(2,d)). { v d
( r(v,d)U :=
|
R
·(v ,d)[U
]|
;:=
u(v,d)^2 ;:=
v^(2*
t(v,d) ) )d , v }.In a binary system.
{ d ( r(2,d)U
:=
|
R
·(2,d)[U
]|
;:=
u(2,d)^2;:=
2^(2*
t(2,d) ):=
)d, v }.
Eg., { r(2, 1)
r(2, 2)
r(2, 3)
r(2, 4)
r(2, 5)
r(2, 6)
r(2, 7)
r(2, 8)
r(2, 9)
r(2, 10)
=
256,r(2, 2)
=
429496 7296,r(2, 3)
=
1.340780 792994 259709 957402 499820 584612 7479 ·(10^ 154),r(2, 4)
=
4.014132 182036 063039 166060 606038 876734 3771 ·(10^ 3.9456 ·(10 ^ 4) ),r(2, 5)
=
9.630350 133920 413014 213703 778052 746804 2213 ·(10^ 2.585827 972 ·(10 ^ 9) ),r(2, 6)
=
3.636549 880934 858190 730055 838296 676980 3584 ·(10^ 1.110604 657704 671426 4 ·(10 ^ 19) ),r(2, 7)
=
2.920966 625003 926469 642581 049794 912721 3645 ·(10^ 2.048703 988774 787275 000242 185002 064654 0026 ·(10 ^ 58) ),r(2, 8)
=
1.438368 435388 603127 724431 746286 617796 3432 ·(10^ 6.971378 424206 523585 973143 140186 083599 3006 ·(10 ^ 76) ),r(2, 9)
=
2.361022 671459 731320 687702 749778 179430 9461 ·(10^ 8.072304 726028 225379 382630 397085 399030 0713 ·(10 ^ 153) ),r(2, 10)
=
5.621813 023170 085026 967697 421355 931681 4924 ·(10^ 1.082319 113185 543439 411173 647035 176687 1783 ·(10 ^ 308) ),..
}.Complexity class.
The set
R
·(v,d)[U
]: remains on the same complexity level asU
·(v,d).2.7.
Minimal inferences, derivations (Semantic).
(1)
As mentioned, a collection
(2)
Each of the subsets in the two components of the derivation can therefore always be reduced according to logical laws to the smallest possible logical-semantic content: in this case, logical relations in a domain with d objects.
We consider the components as mentioned in conjunction.
For convenience, we assume a binary system. This always has two values: valence
The set of possible arguments can therefore be reduced to its paraphrase reduct
version at semantic level.
(v d k1
k2 (
(
(
(
p1
q1 ( (
(p1 := 1,
(q1 := 1,
The paraphrase reduct versions of premise and conclusion will therefore each consist of exactly one element from each of the original subsets
k1, k2, from
This means that the set of all possible unique minimal forms of reasoning under the parameters
{v,d} is formed by a matrix:
{ v d
(
r(v,d)T: The total number of all possible unique minimal reasoning or conclusions.
Obviously, the size of this collection is formed by the Cartesian product (
t(v,d) ·t(v,d)).
{ v d
( r(v,d)T
{ d ( r(2,d)T
The set
(1)
Ultimately, we want to know whether an argument is valid, in other words valid. In other words, which of the derivation relations from the matrix
Each element of the matrix
The total number of all possible unique contradictory reasoning or conclusions is simply the same as that of any set of disjunctions: exactly one.
The total number in the consistent set of all possible unique reasoning or conclusions is therefore simply r (v,d)·(v,d)T -1.
(2)
xT: The total number of all possible unique valid reasonings or conclusions.
The formula for the number of valid derivation relations xT with valence v =2 and number of objects d is:
The values xT·(2,d) largely correspond to the powers of 3 of the powers of 2. See sequence A011764 in the OEIS.
Below is a table with the most important dimensions of the collections mentioned above.
This table shows how combinatorial possibilities in a simple logical system quickly lead to a search space of astronomical proportions. For example, with 100000 items we can make a number of 'minimal arguments' (at the semantic level) whose number consists of a number of digits where just the length of the number can be represented with an exponent (decimal logarithm) which in turn has a length of 30102 digits. In other words, not the number itself is 30102 digits long, but the exponent with which her length can be represented.
To put the above numbers somewhat in perspective, the following are some examples of large numbers occurring in nature (all according to fairly rough estimates).
• The number of galaxy clusters: approx. 4 ·10 ^8.
• The number of galaxies in the universe: approx. 10 ^11.
• The number of stars per galaxy: approx. 10^8 to 10^14.
• The number of stars in 'our' galaxy, the Milky Way: approx. 10^11.
• The number of stars in the observable universe: approx. 10 ^22.
• The number of molecules in the observable universe: approx. 10 ^80.
• The total number of fish in the oceans: approx. 3.5 ·10 ^9.
• The number of ants on Earth: approx. 3.5 ·10 ^12.
• The total number of grains of sand on all beaches on earth: approx. 10 ^21.
• The number of cells in the human body: approx. 10 ^14.
• The number of different proteins that can be built from 100 amino acids: approx. 10 ^130.
To highlight two examples:
With 5 items, you can make almost as many -unique, minimal- arguments as the total number of grains of sand on all beaches on Earth.
With 7 items, which is the average memory capacity of our conscious attention window, you can make almost as many -unique, minimal- arguments as molecules existing in the observable universe.
These -literally- astronomical numbers indicate the level of complexity and thus decision problems.
It does not help to resort to a more advanced logical system. As a general rule, the more advanced the logical system, the more expressive power it has, but the less decision-making power. With each step towards a more advanced logical system, such as modal logic, multivalued logic, predicate logic, etc., and also so-called 'fuzzy logic', the numbers and problems of complexity and decidability are only increasing explosively again!
Clearly, without sufficient knowledge and skills of logical proof and testing, possible arguments about more than two items are already almost impossible to assess.
Derivations are at the semantic level bipartite .
As mentioned, a collection
U
·(v,d) contains subsetsU
·(v,d)[k1] each consisting of unique combinations of logical relations from the collectionT
·(v,d). All those elements have their own logical validity value which is unique withinT
·(v,d). When we combine these values, for example in a premise or conclusion within a derivation, then according to the logical laws at semantic level, the immediate result is paraphrase reduction of the combination to one logical validity value which in turn corresponds to one logical relation inT
·(v,d). This means that as a net result, premise and conclusion each contain (again: at semantic level) only one element. Therefore, at semantic level we can calculate logical derivations as propositions with only two simple elements.(2)
The set of reasonings in their minimal paraphrase form .
Each of the subsets in the two components of the derivation can therefore always be reduced according to logical laws to the smallest possible logical-semantic content: in this case, logical relations in a domain with d objects.
We consider the components as mentioned in conjunction.
For convenience, we assume a binary system. This always has two values: valence
(v
This system has a number of logical relationships as we saw earlier:=
2 ).
(t(v,d)
=
v ^(v ^d ) ).The set of possible arguments can therefore be reduced to its paraphrase reduct
version at semantic level.R
·(v,d)[T
] the set of all possible unique minimal reasoning or conclusions at semantic level.(v d |
(k1
k2 ( R
·(v,d)[U
][k1,k2 ](U
·(v,d)[k1] in conjunctieU
·(v,d)[k2] in conjunctie );(Cj
(U
·(v,d)[k1 ]Cj
(U
·(v,d) [k2] );(U
·(v,d)[k1]syn
par-rdc
U
·(v,d )[k2]syn
par-rdc
);par-rdc
(p1
q1 ( (T
·(v,d)[p1]
T
·(v,d)[q1] );R
·(v,d)[T
] [p1,q1] ;R
·(v,d)[T
]:=
(p1 := 1, ..
u(2,d) )
(q1 := 1, ..
u(2,d) )R
·(v,d) [T
][p1,q1] ) ) );The paraphrase reduct versions of premise and conclusion will therefore each consist of exactly one element from each of the original subsets
k1, k2, from U
·(v,d).This means that the set of all possible unique minimal forms of reasoning under the parameters
{v,d} is formed by a matrix: { v d
( R
·(v,d)[T
]:=
(T
·(v,d)X
T
·(v,d) ) ) d, v }.Size.
r(v,d)T: The total number of all possible unique minimal reasoning or conclusions.
Obviously, the size of this collection is formed by the Cartesian product (
t(v,d) ·t(v,d)). { v d
( r(v,d)T :=
|
R
·(v ,d)[T
]|
;:=
t(v,d)^2 ;:=
v^(2*
b(v,d) ) )d , v }.In a binary system.
{ d ( r(2,d)T
:=
|
R
·(2,d)[T
]|
;:=
t(2,d)^2;:=
t(2,d+1);:=
2^(2*
b(2,d) ):=
A001146(d )^2;:=
A001146(d +1 ) )d }.
Eg., { r(2, 1)T
r(2, 2)T
r(2, 3)T
r(2, 4)T
r(2, 5)T
r(2, 6)T
r(2, 7)T
r(2, 8)T
r(2, 9)T
r(2,10)T
=
16,r(2, 2)T
=
256,r(2, 3)T
=
65536,r(2, 4)T
=
4.294967 296 ·(10^ 9),r(2, 5)T
=
1.844674 407370 955161 6 ·(10^ 19),r(2, 6)T
=
3.402823 669209 384634 633746 074317 682114 56 ·(10^ 38),r(2, 7)T
=
1.157920 892373 161954 235709 850086 879078 5326 ·(10^ 77),r(2, 8)T
=
1.340780 792994 259709 957402 499820 584612 7479 ·(10^ 154),r(2, 9)T
=
1.797693 134862 315907 729305 190789 024733 6179 ·(10^ 308),r(2,10)T
=
3.231700 607131 100730 071487 668866 995196 0444 ·(10^ 616),..
}.Complexity class.
The set
R
·(v,d)[T
]: remains on the same complexity level asT
·(v,d).2.8.
Valid reasonings.
(1)
Evaluation of arguments.
Ultimately, we want to know whether an argument is valid, in other words valid. In other words, which of the derivation relations from the matrix
R
·(v,d)[T
] are valid?Each element of the matrix
R
·(v,d)[T
] is easy to solve like any implication according to the rules of the general truth value table.
See above, 2.4. Truth value table.
Also see: Principles of Logical Proof; (4.1a) Method of Truth Value Tables.
And: Proof Method for Proposition Logic: the Truth Value Table method .
Also see: Principles of Logical Proof; (4.1a) Method of Truth Value Tables.
And: Proof Method for Proposition Logic: the Truth Value Table method .
(1.1)
Each of the logical relationships in the components of
Each of these value patterns is an element of the set (value patterns of) logical relationships
This means, as we have seen, that each of these binary patterns has a length of:
The results again consist of binary truth value patterns.
(1.3)
Rules for interpretation of a binary truth value pattern:
Encoding as binary numbers.
Each of the logical relationships in the components of
R
·(v,d)[T
] can be endoded in the simplest logical system, propoposition logic (PPL), as a binary truth value pattern.Each of these value patterns is an element of the set (value patterns of) logical relationships
T
·( v,d)[k1].This means, as we have seen, that each of these binary patterns has a length of:
b(v,d)·(v,d)
(1.2) =
v·^d .Paraphrase reduction to one binary number.
The results again consist of binary truth value patterns.
(1.3)
Interpretation of the binary outcome.
Rules for interpretation of a binary truth value pattern:
(a) Not all bits are set to 0 or 1 : undecided, indefinite contingency.
(b) All bits are set to 0 or 1 : decided.
(b) All bits are set to 0 or 1 : decided.
(b1) All bits are set to 0: contradiction (non-satisfiability).
Only true if 'true implies false' (i.e.
(b2) Not all bits are set to 0, and neither are they to 1 : (definitite) contingency.
Only true if 'true implies false' (i.e.
$
1 $
0 ).(b2) Not all bits are set to 0, and neither are they to 1 : (definitite) contingency.
(b2.1) Not all bits are set to 0 : consistency (satisfiability).
(b2.2) Not all bits are set to 1 : invalidity (presupposition, c.q. fallacy).
(b3) All bits are set to 1: validity.(b2.2) Not all bits are set to 1 : invalidity (presupposition, c.q. fallacy).
The total number of all possible unique contradictory reasoning or conclusions is simply the same as that of any set of disjunctions: exactly one.
The total number in the consistent set of all possible unique reasoning or conclusions is therefore simply r (v,d)·(v,d)T -1.
(2)
The valid reasoning.
Size.
xT: The total number of all possible unique valid reasonings or conclusions.
The formula for the number of valid derivation relations xT with valence v =2 and number of objects d is:
x(v,d)T
=
(v +1)·^b(v,d );=
(v +1)·^(v·^d);In a binary system.
The values xT·(2,d) largely correspond to the powers of 3 of the powers of 2. See sequence A011764 in the OEIS.
Eg., { x(2, 1)T
x(2, 2)T
x(2, 3)T
x(2, 4)T
x(2, 5)T
x(2, 6)T
x(2, 7)T
x(2, 8)T
x(2, 9)T
x(2,10)T
=
9,x(2, 2)T
=
81,x(2, 3)T
=
6561,x(2, 4)T
=
4.304672 1 ·(10 ^7 ),x(2, 5)T
=
1.853020 188851 841 ·(10 ^15 ),x(2, 6)T
=
3.433683 820292 512484 657849 089281 ·(10 ^30 ),x(2, 7)T
=
1.179018 457773 858317 152087 286141 251866 5678 ·(10 ^61 ),x(2, 8)T
=
1.390084 523771 447327 649397 867896 613031 1422 ·(10 ^122 ),x(2, 9)T
=
1.932334 983228 891510 545406 872201 958105 5401 ·(10 ^244 ),x(2,10)T
=
3.733918 487410 200435 329597 541848 665882 2541 ·(10 ^488 ),..
}.The same sequence as percentages valid implications:
{ 56.25%,
31.640625%,
10.011291 503906 25%,
1.002259 575761 854648 590087 890625%,
1.004524 257206 332858 195774 182519 244277 5005 ·(10 ^-002)%,
1.009068 983315 934771 190166 090841 089949 3574 ·(10 ^-006)%,
1.018220 213090 254245 618211 973419 191101 3791 ·(10 ^-014)%,
1.036772 402345 562763 403206 053360 190738 2718 ·(10 ^-030)%,
1.074897 014265 389476 630012 892337 230410 6700 ·(10 ^-062)%,
1.155403 591276 648908 023678 855815 537058 0566 ·(10 ^-126)%,
31.640625%,
10.011291 503906 25%,
1.002259 575761 854648 590087 890625%,
1.004524 257206 332858 195774 182519 244277 5005 ·(10 ^-002)%,
1.009068 983315 934771 190166 090841 089949 3574 ·(10 ^-006)%,
1.018220 213090 254245 618211 973419 191101 3791 ·(10 ^-014)%,
1.036772 402345 562763 403206 053360 190738 2718 ·(10 ^-030)%,
1.074897 014265 389476 630012 892337 230410 6700 ·(10 ^-062)%,
1.155403 591276 648908 023678 855815 537058 0566 ·(10 ^-126)%,
..
}.2.9.
Table of dimensions.
Below is a table with the most important dimensions of the collections mentioned above.
|
Combinatory explosion in logical system (PPL) |
|||||
|---|---|---|---|---|---|
|
Truth values (valence) v =2 (Binary system) |
|||||
| items |
Domain states (pattern length) |
Logical relations (formulas) | Tupels (pairs) of formulas | Valid implications (amount) | Valid implications (ppt.) |
| d | b(v,d) | t(v,d) | r(v,d)T | x(v,d)T | %(x/t)(v,d)T |
|
1 |
2 |
4 |
16 |
9 | 56.25% |
|
2 |
4 |
16 |
256 |
81 |
31.640 625% |
|
3 |
8 |
256 |
65536 |
6561 |
10.011291 503906 25% |
|
4 |
16 |
65536 |
429496 7296 |
430467 21 |
1.002259 575761 854649% |
|
5 |
32 |
429496 7296 |
1.844674 407371 955162 ·(10 ^019 [ 2] ) |
1.853020 188851 841 ·(10 ^015 [ 2] ) |
1.004524 257206 332858 ·(10 ^-002 )% |
|
6 |
64 |
1.844674 407370 955162 ·(10 ^019 [ 2] ) |
3.402823669 209384635 ·(10 ^038 [ 2] ) |
3.433683 820292 512485 ·(10 ^030 [ 2] ) |
1.009068 983315 934771 ·(10 ^-006 )% |
|
7 |
128 |
3.402823 669209 384635 ·(10 ^038 [ 2] ) |
1.157920 892373 161954 ·(10 ^077 [ 2] ) |
1.179018 457773 858317 ·(10 ^061 [ 2] ) |
1.018220 213090 254246 ·(10 ^-014 [ 2] )% |
|
8 |
256 |
1.157920 892373 161954 ·(10 ^077 [ 2] ) |
1.340780792 994259710 ·(10 ^154 [ 3] ) |
1.390084 523771 447328 ·(10 ^122 [ 3] ) |
1.036772 402345 562763 ·(10 ^-030 [ 2] )% |
|
9 |
512 |
1.340780 792994 ·(10 ^154 [ 3] ) |
1.797693 134862 315907 ·(10 ^308 [ 3] ) |
1.932334 983228 891511 ·(10 ^244 [ 3] ) |
1.074897 014265 389476 ·(10 ^-062 [ 2] )% |
|
10 |
1024 |
1.797693 134862 315907 ·(10 ^308 [ 3] ) |
3.231700 607131 100730 ·(10 ^616 [ 3] ) |
3.733918 487410 200435 ·(10 ^488 [ 3] ) |
1.155403 591276 648908 ·(10 ^-126 [ 3] )% |
|
10 ^2 |
1.267650 600228 229401 ·(10 ^30 [ 2] ) |
2.285367 694229 513703 ·(10 ^3.816008 546901 470562 ·(10 ^29 [ 2] ) ) |
5.222905 497827 924040 ·(10 ^7.632017 093802 941125 ·(10 ^29 [ 2]) ) |
2.561263 804102 827066 ·(10 ^6.048230 449270 260188 ·(10 ^29 [ 2]) ) |
4.903906 082865 165216 ·(10 ^-1.583786 644532 680936 ·(10 ^29 [ 2]) ) % |
|
10 ^3 |
1.071508 607186 267321 ·(10 ^301 [ 3] ) |
7.096672 219435 693805 ·(10 ^3.225562 313752 005814 ·(10 ^300 [ 3] ) ) |
5.036275 659011 033621 ·(10 ^6.451124 627504 011628 ·(10 ^300 [ 3] ) ) |
1.296912 946078 858393 ·(10 ^5.112395 311036 297716 ·(10 ^300 [ 3] ) ) |
2.575142 891073 463136 ·(10 ^-1.338729 316467 713912 ·(10 ^300 [ 3] ) )% |
|
10 ^4 |
1.995063 116880 758385 ·(10 ^3010 [ 4] ) |
6.467855 830387 433571 ·(10 ^(6.005738 414239 835051 ·(10 ^3009 [ 4] ) ) |
4.183315 904267 671786 ·(10 ^(1.201147 682847 967010 ·(10 ^3010 [ 4] ) ) |
1.968225 299623 265918 ·(10 ^(9.518870 175710 679943 ·(10 ^3009 [ 4] ) ) |
4.704940 637199 671382 ·(10 ^(-2.492606 652768 990158 ·(10 ^3009 [ 4] ) ) % |
|
10 ^5 |
9.990020 930143 845079 ·(10 ^30102 [ 5] ) |
1.022672 567782 053958 ·(10 ^(+3.007295 957284 283071 ·(10 ^30102 [ 5] ) ) % |
1.045859 180893 939748 ·(10 ^(+6.014591 914568 566142 ·(10 ^30102 [ 5] ) ) % |
1.376624 183690 244770 ·(10 ^(+4.766451 320865 920576 ·(10 ^30102 [ 5] ) ) % |
1.316261 509043 298055 ·(10 ^(-1.248140 593702 645566 ·(10 ^30102 [ 5] ) ) % |
This table shows how combinatorial possibilities in a simple logical system quickly lead to a search space of astronomical proportions. For example, with 100000 items we can make a number of 'minimal arguments' (at the semantic level) whose number consists of a number of digits where just the length of the number can be represented with an exponent (decimal logarithm) which in turn has a length of 30102 digits. In other words, not the number itself is 30102 digits long, but the exponent with which her length can be represented.
2.10.
Numbers for comparision.
To put the above numbers somewhat in perspective, the following are some examples of large numbers occurring in nature (all according to fairly rough estimates).
In the universe.
• The number of galaxy clusters: approx. 4 ·10 ^8.
• The number of galaxies in the universe: approx. 10 ^11.
• The number of stars per galaxy: approx. 10^8 to 10^14.
• The number of stars in 'our' galaxy, the Milky Way: approx. 10^11.
• The number of stars in the observable universe: approx. 10 ^22.
• The number of molecules in the observable universe: approx. 10 ^80.
On Earth.
• The total number of fish in the oceans: approx. 3.5 ·10 ^9.
• The number of ants on Earth: approx. 3.5 ·10 ^12.
• The total number of grains of sand on all beaches on earth: approx. 10 ^21.
In the human body.
• The number of cells in the human body: approx. 10 ^14.
• The number of different proteins that can be built from 100 amino acids: approx. 10 ^130.
To highlight two examples:
With 5 items, you can make almost as many -unique, minimal- arguments as the total number of grains of sand on all beaches on Earth.
With 7 items, which is the average memory capacity of our conscious attention window, you can make almost as many -unique, minimal- arguments as molecules existing in the observable universe.
These -literally- astronomical numbers indicate the level of complexity and thus decision problems.
It does not help to resort to a more advanced logical system. As a general rule, the more advanced the logical system, the more expressive power it has, but the less decision-making power. With each step towards a more advanced logical system, such as modal logic, multivalued logic, predicate logic, etc., and also so-called 'fuzzy logic', the numbers and problems of complexity and decidability are only increasing explosively again!
Clearly, without sufficient knowledge and skills of logical proof and testing, possible arguments about more than two items are already almost impossible to assess.
C.P. van der Velde © 2014, 2018, 2024.