Methode Formele Logica
Schema's
Logische niveau's en criteria
Inhoudsopgave
1. Niveau I: Waarheid / onwaarheid van beweringen
2. Niveau II: Vervulbaarheid / geldigheid
2.1. Waarheidswaarden-tabel voor PPL - tweewaardig, voor twee variabelen.
2.2. Waarheidswaarden-tabel PDL - tweewaardig, voor twee variabelen.
2.3. Waarheidsgehalte en logische kracht.
2.4. Formules in gestandaardiseerde vorm.
2.5. Het beoordelen van theorieën (verzamelingen van proposities).
2.6. Contingentie en Vooronderstelling.
2.7. Elementaire Geldige en Ongeldige afleidingen.
2.8. Geldigheid, Vervulbaarheid en Contingentie.
2.9. Relaties tussen logische criteria van niveau II.
2.2. Waarheidswaarden-tabel PDL - tweewaardig, voor twee variabelen.
2.3. Waarheidsgehalte en logische kracht.
2.4. Formules in gestandaardiseerde vorm.
2.5. Het beoordelen van theorieën (verzamelingen van proposities).
2.6. Contingentie en Vooronderstelling.
2.7. Elementaire Geldige en Ongeldige afleidingen.
2.8. Geldigheid, Vervulbaarheid en Contingentie.
2.9. Relaties tussen logische criteria van niveau II.
4. Tabel met Enkele Mijlpalen in de Meta-logica
5. Criteria in de formele logica
Meta-waarheid: logische criteria
Logische kwaliteit |
|---|
Niveau I:
Waarheid / onwaarheid
van beweringen
1.1. Waarheidswaarden-tabel voor PPL - tweewaardig.
In een formeel logisch systeem worden alle mogelijke logische relaties bij een gekozen vocabulaire volledig gedefinieerd door middel van de waarheidswaarden-tabel.
De waarheidswaarden-tabel voor het meest simpele logische systeem, de propositielogica (PPL), dekt - bij elk gekozen formalisme of format - hoe dan ook alle basiscombinaties die in het meest elementaire begin van elke vorm van redenering een rol spelen. Ze vormt daardoor echt de allereerste, noodzakelijke grondslag voor correct combinatorisch denken.
Waarheidswaarden-tabel PPL - voor één variabele.
Deze waarheidswaarden-tabel bevat alle mogelijke volgordes van waarden van twee variabelen (proposities) in de PPL, die twee waarden kunnen aannemen.
De grondslag bestaat uit 1 variabele x 2 waarden = 2 basiscombinaties. Daarmee zijn 2 volgordes mogelijk, of reeksen van waarheidswaarden: waarvan elk een unieke logische relatie weergeeft. Hierdoor ontstaat de onderstaande meest eenvoudige tabel van 2 rijen bij 2 kolommen is 4 cellen.
| 1 | 2 |
|---|---|
| 1 | 0 |
| 0 | 1 |
| T | F |
| A | ¬A |
| ¬B | B |
Waarheidswaarden. |
||
|---|---|---|
1 |
± |
0 |
Waar,verum: Verificatie. |
Onbepaald,ongeïnterpreteerd: Indefiniet. |
Onwaar,falsum: Falsificatie. |
Waarheidswaarde(value, valor): |
||
$(G)=1. |
(0 <$(G)<1). |
$(G)=0. |
Waarheidswaardetoekenning(valuatie): |
||
|
V!(G) :=1. |
¬V!(G)  {0,1}. |
V!(G) :=0. |
Waarheidswaardebepaling(evaluatie), via eindig bewijs: |
||
 i E![i]  G. |
(¬i E![i] G) 
(¬j E![j] ¬G). |
i E![i] ¬G. |
Interpretatie(denotatie, assignment): |
||
m M![m] G. |
(¬m M![m]G)
(¬n M![n]¬G). |
m M![m] ¬G. |
Niveau II:
Vervulbaarheid / geldigheid
2.1. Waarheidswaarden-tabel voor PPL - tweewaardig.
Waarheidswaarden-tabel PPL - met twee variabelen.
Deze waarheidswaardentabel bevat alle mogelijke volgordes van waarheidswaarden bij de combinatie van twee variabelen die elk twee waarden kunnen aannemen. Deze uitgangsgegevens leveren allereerst 2 waarden keer 2 variabelen = 4 combinaties, oftewel mogelijke (individuele) objecttoestanden.
De grondslag voor de tabel bestaat uit 2 waarden tot de macht 2 variabelen = 4 toestandcombinaties, oftewel mogelijke domeintoestanden.
Daarmee zijn 2 tot de macht 4 = 16 volgordes mogelijk, of reeksen van waarheidswaarden, oftewel mogelijke (domein)toestandsrelaties , waarvan elk een unieke logische relatie weergeeft.
Hierdoor ontstaat de onderstaande tabel van 4 kolommen bij 16 rijen is 64 cellen.
Tabel tweewaardige waardencombinaties |
||||||||
|---|---|---|---|---|---|---|---|---|
| Nr. | Waarde- patroon |
Logische relatie in PPL |
Logische kracht | |||||
| 1 | 1 | 1 | 1 | 1 |
T |
¬F |
X ¬X |
0 |
| 2 | 0 | 0 | 0 | 0 |
F |
¬T |
X ¬X |
1 |
| 3 | 1 | 1 | 0 | 0 |
A |
¬¬A |
0.50 | |
| 4 | 1 | 0 | 1 | 0 |
B |
¬¬B |
0.50 | |
| 5 | 0 | 0 | 1 | 1 |
¬A |
¬A |
0.50 | |
| 6 | 0 | 1 | 0 | 1 |
¬B |
¬B |
0.50 | |
| 7 | 1 | 0 | 0 | 0 |
A B |
¬(¬A ¬B) |
0.75 | |
| 8 | 0 | 1 | 0 | 0 |
A ¬B |
¬(¬A B) |
0.75 | |
| 9 | 0 | 0 | 1 | 0 |
¬A B |
¬(A ¬B) |
0.75 | |
| 10 | 0 | 0 | 0 | 1 |
¬A ¬B |
¬(A B) |
A\B |
0.75 |
| 11 | 1 | 1 | 1 | 0 |
A B |
¬(¬A ¬B) |
0.25 | |
| 12 | 1 | 1 | 0 | 1 |
A ¬B |
¬(¬A B) |
A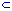 B |
0.25 |
| 13 | 1 | 0 | 1 | 1 |
¬A B |
¬(A ¬B) |
A B |
0.25 |
| 14 | 0 | 1 | 1 | 1 |
¬A ¬B |
¬(A B) |
A|B |
0.25 |
| 15 | 1 | 0 | 0 | 1 |
A B |
¬(A#B) |
0.50 | |
| 16 | 0 | 1 | 1 | 0 |
A#B |
¬(A B) |
0.50 | |
|
{Naar: Benjamin Peirce (1809-1880), Friedrich Wilheml Karl Ernst Schröder (1841-1902), e.a..} |
||||||||
|
{Zie: Bewijsmethode voor Propositielogica: de Waarheidswaarden- tabelmethode
.} |
||||||||
2.2. Waarheidswaarden-tabel voor PDL - tweewaardig.
Waarheidswaarden-tabel voor PDL - met twee variabelen.
In de predikatenlogica (PDL) kunnen eigenschappen (predikaten) worden toegepast op verschillende domein-elementen (via objectvariabelen, objectconstanten, en logische functies). Hierdoor nemen de combinatorische mogelijkheden nog eens hyper-exponentieel toe.
In PDL worden vervolgens kwantoren toegepast op geprediceerde objectvariabelen, om regelmatige relaties tussen predicatie s van dezelfde predicaatnaam op dezelfde variabelenaam compact weer te geven (conjunctieve relaties via universele kwantor, disjunctieve relaties via existentiële kwantor). Maar voordat we die regelmatigheden kunnen vinden, hebben we nog steeds te maken met die combinatorische explosie.
Hieronder een uiterst simpel voorbeeld: voor een tweewaardig systeem, met een 'minuscule' omvang: één predicaat, van ariteit één, en een domein van slechts twee elementen. Daarmee komen we alweer op 16 mogelijke logische relaties.
Tabel tweewaardige waardencombinaties |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nr. | Waarde- patroon |
Logische relatie in PPL |
Logische relatie in PDL |
Logische relatie in Sk |
Logische kracht | ||||||
| 1 | 1 | 1 | 1 | 1 |
T |
¬F |
X ¬X |
0 | |||
| 2 | 0 | 0 | 0 | 0 |
F |
¬T |
X ¬X |
1 | |||
| 3 | 1 | 1 | 0 | 0 |
A1 |
¬¬A1 |
0.50 | ||||
| 4 | 1 | 0 | 1 | 0 |
A2 |
¬¬A2 |
0.50 | ||||
| 5 | 0 | 0 | 1 | 1 |
¬A1 |
¬A1 |
0.50 | ||||
| 6 | 0 | 1 | 0 | 1 |
¬A2 |
¬A2 |
0.50 | ||||
| 7 | 1 | 0 | 0 | 0 |
A1 A2 |
¬(¬A1 ¬A2) |
 x A[x] |
¬x ¬A[x] |
A[x] |
0.75 | |
| 8 | 0 | 1 | 0 | 0 |
A1 ¬A2 |
¬(¬A1 A2) |
0.75 | ||||
| 9 | 0 | 0 | 1 | 0 |
¬A1 A2 |
¬(A1 ¬A2) |
0.75 | ||||
| 10 | 0 | 0 | 0 | 1 |
¬A1 ¬A2 |
¬(A1 A2) |
A1\A2 |
¬x A[x] |
x ¬A[x] |
¬A[x] |
0.75 |
| 11 | 1 | 1 | 1 | 0 |
A1 A2 |
¬(¬A1 ¬A2) |
x A[x] |
¬x ¬A[x] |
A[cs] |
0.25 | |
| 12 | 1 | 1 | 0 | 1 |
A1 ¬A2 |
¬(¬A1 A2) |
A1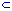 A2 |
0.25 | |||
| 13 | 1 | 0 | 1 | 1 |
¬A1 A2 |
¬(A1 ¬A2) |
A1 A2 |
0.25 | |||
| 14 | 0 | 1 | 1 | 1 |
¬A1 ¬A2 |
¬(A1 A2) |
A1|A2 |
¬x A[x] |
x ¬A[x] |
¬A[cs] |
0.25 |
| 15 | 1 | 0 | 0 | 1 |
A1 A2 |
¬(A1#A2) |
(A1 A2)
(¬A1 ¬A2) |
0.50 | |||
| 16 | 0 | 1 | 1 | 0 |
A1#A2 |
¬(A1 A2) |
(A1 ¬A2)
(¬A1 A2) | 0.50 | |||
2.3. Waarheidsgehalte en logische kracht.
Logische kracht is omgekeerd evenredig aan waarheid.
Gegeven een formule F - d.i. een mogelijke logische relatie onder formeel systeem
L!
- uit verzameling T* (met omvang t=
v**(v**d)).Hiervoor geldt:
(a)
F is afleidbaar uit de maximale logische kracht in
{ j ( (F[j]
T*) 
($0 F[j]) )
j;
j ($0 F
[j]) j;
($0 ( j 
F[j]) );
($0 ( j F
[j]) );
($0 ( j 
F[j]) );
($0 (T*
)) }.
(b)
Uit F is de minimale logische kracht in
{ j ( (F[j]
T*) (F[j]
j (F[j]
(( j F
[j])
(( j F
[j])
((j F[j])
((T*)
(c)
Combinatie van (a) en (b).
{ j ( (F[j]
T*) ( ($0 F[j])
(F[j]
j ( ($0 F
[j]) (F[j]
( ($0 (j
F[j]) ) ( (j
F[j])
( ($0 (j
F[j]) ) ( (j
F[j])
( ($0 (j F
[j]) ) ( (j F[j])
( ($0 (j
F[j]) ) ( (j
F[j])
( ($0 (T*
)) ( (T*)
($0
Logische kracht en contradictie.
F is afleidbaar uit de maximale logische kracht in
L!
: d.i. contradictie (onwaarheid onder alle omstandigheden); oftewel onwaarheid; oftewel waarheidswaarde$
0.{ j ( (F[j]
T*) ($0 F[j]) )
j;j ($0 F
[j]) j;($0 ( j
F[j]) );($0 ( j F
[j]) );($0 ( j
F[j]) );($0 (T*
)) }.Logische kracht en waarheid.
Uit F is de minimale logische kracht in
L!
afleidbaar: d.i. geldigheid (waarheid onder alle omstandigheden); oftewel waarheid; oftewel waarheidswaarde$
1.{ j ( (F[j]
T*) (F[j] $
1) )j;j (F[j]
$
1) j;(( j F
[j]) $
1 );(( j F
[j]) $
1 );((j F[j])
$
1 );((T*) $
1 ) }.Contradictie, Logische kracht en waarheid.
Combinatie van (a) en (b).
{ j ( (F[j]
T*) ( ($0 F[j])
(F[j] $
1) ) )j ;j ( ($0 F
[j]) (F[j] $
1 ) )j; ( ($0 (j
F[j]) ) ( (j
F[j]) $
1 ) ); ( ($0 (j
F[j]) ) ( (j
F[j]) $
1 ) ); ( ($0 (j F
[j]) ) ( (j F[j])
$
1 ) ); ( ($0 (j
F[j]) ) ( (j
F[j]) $
1 ) ); ( ($0 (T*
)) ( (T*)
$
1) );($0 $
1) }.2.4. Formules in gestandaardiseerde vorm.
In de formele logica wordt een verzameling van logische formules een theorie genoemd. De formules in de verzameling staan in de regel voor beweringen of redeneringen (proposities).
Er bestaan in de formele logica een aantal gestandaardiseerde vormen waarmee formules of verzamelingen van formules helder, eenduidig en compact kunnen worden weergegeven, waardoor ze efficiënt bewerkt en beoordeeld kunnen worden, zgn. normaalvormen.
Een handige vorm voor formules wanneer we ze willen beoordelen is de Conjunctief Normaal Vorm (
CNV
), of Conjunctive Normal Form (CNF
). Een formule inCNF
heeft de vorm van een conjunctie van disjuncties. Met andere woorden, op de hoofdlijn van redenering bestaat een nevenstelling van één of meer conjuncten, waarbij elke conjunct bestaat uit een disjunctie samengesteld uit minstens één enkelvoudige formule (atoom of literaal).Een
CNF
maakt daardoor uitsluitend gebruik van de connectieven {¬,,
}.Algemene structuur van een CNF
verzameling:
{ (T* =
WFF*(L!
PDl)); ( k ( (K*[k] 
CNF
*(T*))(K*[k] =
{ [ F[1]
[ F[2] .. ] ] F[n[k]] } )(n[k] =
|
K*[k]|
) )(K*[k] =
{
(j[k]=1,..n[k]) F[j[k]] } ) ( ( j ( (F[j]
K*[k])F[j] =
{ [ G[j,1]
[ G[j,2] .. G[m[j[k]]] ] ] } )(m[j[k]] =
|
F[j] | ) ( (F[j] =
{
(h[j[k]]=1,..h[n[k]]) G[h[j[k]]]) } ) ( (0 >
j[k]≥
n[k] )
(0 >
h[j[k]]≥
m[j[k]]) ) ) )j )k ) }.2.5. Het beoordelen van theorieën (verzamelingen van proposities).
Hoe kunnen we de logische 'status', c.q. de semantische waarde, van zo'n verzameling beoordelen? Dit is afhankelijk van het formele systeem, c.q. de logische taal waarin de verzameling geformuleerd is.
We zullen hier alleen enkele randvoorwaarden noemen die het meest algemeen gelden voor het beoordelen van een verzameling formules.
Algemene vereisten voor beoordeling van een theorie :
(a)
{ k ( (K*[k]
( ( ( j ( (F[j]
K*[k])
( (F[j]
( (
( h ( (G[h[j[k]]] F[j
]) (G[h[j[k]]]
) (K*[k]
(b)
{ k ( (K*[k]
( ( ( j ( (F[j]
K*[k])
( (F[j]
( (
( h ( (G[h[j[k]]] F[j
]) (G[h[j[k]]]
) (K*[k]
(c)
Noch (a) noch (b).
De verzameling is geldig (behelst tautologie).
{ k ( (K*[k]
CNF
*(T*)) ( (|
K*[k])|
>
1) ( j ( (F[j]
K*[k]) ( (F[j]$
=
1) ( (|
F[j])|
>
1)
( h ( (G[h[j[k]]] F[j
]) (G[h[j[k]]]$
=
1) )h ) ) ) )j )(K*[k]$
=
1) )k }.(b)
De verzameling is inconsistent (bevat contradictie).
{ k ( (K*[k]
CNF
*(T*)) ( (|
K*[k]|
=
0) ( j ( (F[j]
K*[k]) ( (F[j]$
=
0) ( (|
F[j]|
>
1)
( h ( (G[h[j[k]]] F[j
]) (G[h[j[k]]]$
=
0) )h ) ) ) )j )(K*[k]$
=
0) )k }.(c)
De verzameling is contingent (is onbeslist).
Noch (a) noch (b).
2.6. Contingentie en Vooronderstelling.
Contingentie.
In de meest algemene zin betekent 'contingent' onbepaald, welke betekenis op haar beurt diverse schakeringen kan hebben: niet welbepaald, ongedetermineerd, (nog) niet vaststaand, voorwaardelijk, dus nader te bepalen; ook: niet noodzakelijk (het geval), niet inherent, niet essentieel; soms ook: 'toevallig' c.q. onderhevig aan toeval, accidentie, coïncidentie en dergelijke.
In de formele logica kunnen we twee betekenissen van de term contingentie onderscheiden die volkomen exact zijn te definiëren.
(1)
Contingent in de zin van subspecifiek onbepaald, c.q. indefiniet. Dat wil zeggen: (geheel) onbeslist wat betreft de waarheidswaarde.
(Niet te verwarren met indefiniet in wiskundige, algebraïsche zin).
De waarheidswaarde kan dus in principe nog 'vrij' variëren over de gehele waardenschaal, dat is in een binair systeem van 0[00..] (onwaar, contradictie) tot en met 1[11..] (waar, valide, tautologie), dus inclusief deze beide extremen.
{ j (I-CONTIN(F[j] )
((0[00..) ≤
(
Een bewering of redenering die indefiniet-contingent is, is dus (nog) niet gevalueerd. Ze hoeft dus niet per se (eindig
-)bewijsbaar te zijn.
Ze hoeft zelfs niet beslisbaar te zijn.
Ze hoeft dus ook niet gevalideerd c.q. geldig te zijn.
Ze hoeft ook zeker niet consistent te zijn.
(2)
Contingent in de zin van specifiek onbepaald, c.q. definiet dat wil zeggen (geheel) beslist wat betreft de waarheidswaarde.
De waarheidswaarde ligt hier echter tussen de uiterste waarden van de waardenschaal, dat is in een binair systeem als het ware 'ingesloten' tussen 0[00..] (onwaar, contradictie) tot 1[11..] (waar, valide, tautologie), dus exclusief deze beide uitersten.
{ j (D-CONTIN(F[j] )
((0[00..) <
(
Een bewering of redenering die definiet-contingent is, is dus - wat betreft waarheid/geldigheid - wèl gevalueerd.
Ze is daarbij echter niet (eindig-)bewijsbaar gebleken.
Daarmee is ze dus al beslisbaar gebleken.
Ze is daarbij niet gevalideerd kunnen worden, dus wèl bewezen ongeldig.
En daarnaast is ze consistent, waarmee ze bovendien, volgens de Consistentiestelling (zie 2.8) vervulbaar is.
Tenzij anders vermeld wordt 'contingent' hieronder gebruikt in de zin van 'definiet-contingent', oftewel 'contingent-ongeldig
'.Indefiniet-contingent.
Contingent in de zin van subspecifiek onbepaald, c.q. indefiniet. Dat wil zeggen: (geheel) onbeslist wat betreft de waarheidswaarde.
(Niet te verwarren met indefiniet in wiskundige, algebraïsche zin).
De waarheidswaarde kan dus in principe nog 'vrij' variëren over de gehele waardenschaal, dat is in een binair systeem van 0[00..] (onwaar, contradictie) tot en met 1[11..] (waar, valide, tautologie), dus inclusief deze beide extremen.
{ j (I-CONTIN(F[j] )((0[00..) ≤ $
(F[j]) ≤ (1[11..]) );($
(F[j]) [
0[00..] .. 1[11..]]
) }.Ze hoeft zelfs niet beslisbaar te zijn.
Ze hoeft dus ook niet gevalideerd c.q. geldig te zijn.
Ze hoeft ook zeker niet consistent te zijn.
(2)
Definiet-contingent, oftewel Contingent-ongeldig.
Contingent in de zin van specifiek onbepaald, c.q. definiet dat wil zeggen (geheel) beslist wat betreft de waarheidswaarde.
De waarheidswaarde ligt hier echter tussen de uiterste waarden van de waardenschaal, dat is in een binair systeem als het ware 'ingesloten' tussen 0[00..] (onwaar, contradictie) tot 1[11..] (waar, valide, tautologie), dus exclusief deze beide uitersten.
{ j (D-CONTIN(F[j] )((0[00..) < $
(F[j]) < (1[11..]) );($
(F[j]) <
0[00..] .. 1[11..]>
) }.Ze is daarbij echter niet (eindig-)bewijsbaar gebleken.
Daarmee is ze dus al beslisbaar gebleken.
Ze is daarbij niet gevalideerd kunnen worden, dus wèl bewezen ongeldig.
En daarnaast is ze consistent, waarmee ze bovendien, volgens de Consistentiestelling (zie 2.8) vervulbaar is.
Vooronderstelling.
Te onderscheiden zijn:
(1) Logische vooronderstelling: is wat de gronden voor een ongeldige redeneervorm compleet maakt waardoor deze laatste geldig wordt.
Ze is enkel gebonden aan universele abstracte patronen volgens de wetmatigheden van semantiek, syntax en vocabulaire binnen een systeem van de (formele, of combinatorische) logica.
(2) Taalkundige vooronderstelling: is iets anders, nl. wat een taaluiting of tekengeving impliceert ongeacht haar waarheidsgehalte (is a.h.w. een consequens in termines).
Deze is gebonden aan taalvormen c.q. symbolen volgens de conventionele regels van syntax en lexicon van een (menselijk) taalsysteem.
Beide zijn dus niet direct fysisch-gebonden (dus niet aan tijd, ruimte, energie, materie).
(3) Een vooroordeel is een interne, mentale of psychische inhoud, m.n. van cognitieve aard.
Deze is dan ook gebonden aan persoon of groep (performatief, auteur, bron), en daardoor tenminste deels en op de eerste plaats - via neuro-physiologie - fysisch-gebonden. Ze is daarmee in wezen incidenteel van aard (hoewel mogelijk relatief langdurig). Ze gaat in tijd vooraf aan conclusies, beslissingen, uitspraken, handelen, e.d..
Ze is enkel gebonden aan universele abstracte patronen volgens de wetmatigheden van semantiek, syntax en vocabulaire binnen een systeem van de (formele, of combinatorische) logica.
(2) Taalkundige vooronderstelling: is iets anders, nl. wat een taaluiting of tekengeving impliceert ongeacht haar waarheidsgehalte (is a.h.w. een consequens in termines).
Deze is gebonden aan taalvormen c.q. symbolen volgens de conventionele regels van syntax en lexicon van een (menselijk) taalsysteem.
Beide zijn dus niet direct fysisch-gebonden (dus niet aan tijd, ruimte, energie, materie).
(3) Een vooroordeel is een interne, mentale of psychische inhoud, m.n. van cognitieve aard.
Deze is dan ook gebonden aan persoon of groep (performatief, auteur, bron), en daardoor tenminste deels en op de eerste plaats - via neuro-physiologie - fysisch-gebonden. Ze is daarmee in wezen incidenteel van aard (hoewel mogelijk relatief langdurig). Ze gaat in tijd vooraf aan conclusies, beslissingen, uitspraken, handelen, e.d..
Enkele onderlinge relaties.
(·) Elke concrete taaluiting kan een taalkundige vooronderstelling impliceren.
(·) Een taalkundige vooronderstelling kan voortkomen uit een tevoren aanwezige psychische/ cognitieve inhoud (of, niet zelden, een gebrek daaraan).
(·) Een psychische/ cognitieve inhoud kan geheel of gedeeltelijk voortkomen uit een tevoren aanwezige vooroordeel.
(·) Een vooroordeel kan voortvloeien uit een ongeldige redenering.
(·) Een ongeldige redenering impliceert noodzakelijk en tegelijk een logische vooronderstelling: d.i. contradictie of definiet-contingentie.
Merk op dat alleen de laatste relatie noodzakelijk altijd geldt, en ook expliciet, compleet, exact en met zekerheid afleidbaar kan zijn ..
(hoewel dat afhankelijk is van eindig-bewijsbaarheid en beslisbaarheid).(·) Een taalkundige vooronderstelling kan voortkomen uit een tevoren aanwezige psychische/ cognitieve inhoud (of, niet zelden, een gebrek daaraan).
(·) Een psychische/ cognitieve inhoud kan geheel of gedeeltelijk voortkomen uit een tevoren aanwezige vooroordeel.
(·) Een vooroordeel kan voortvloeien uit een ongeldige redenering.
(·) Een ongeldige redenering impliceert noodzakelijk en tegelijk een logische vooronderstelling: d.i. contradictie of definiet-contingentie.
Definiet-contingentie, formeel.
Een formule F[j] is definiet-contingent:
• F[j] is vervulbaar, maar ongeldig;
• F[j] is noch waar, noch onwaar;
• Het waarheidswaardepatroon c[t] van F[j] ligt tussen
• F[j] is noch waar, noch onwaar;
• Het waarheidswaardepatroon c[t] van F[j] ligt tussen
$
0[00..] en$
1[11..];
(·) Er bestaat een formule X[i]) die logisch equivalent is aan F[j], èn die syntactisch
identiek is aan de maximaal semantische reduct van F[j], d.i. F[j]·
(·) Er bestaat een interpretatie c.q. model
equiv-rdc
;
Dus: De aanname van X[i] vervult F[j]) ;
M.a.w.: F[j] vooronderstelt X[i]) ;
M.a.w.: F[j] vooronderstelt X[i]) ;
M
![m] die X[i] is of omvat, en waaronder F[j] (dus) geldig is.{ j ( D-CONTIN(F[j] );
• {SATBL(F[j] ) ¬TAUT(F
[j] ) };
•( ((¬ F[j])
(¬ ¬F[j]));
• ( t ( (F[j]$ = c
[t]) (
{SATBL(F[j] ) ¬TAUT(F
[j] ) };•
( ((¬ F[j])
(¬ ¬F[j]));•
( t ( (F[j]$ = c
[t]) ($
0<
c[t]<
$
1) )t;
(·) ( i ( ( (F[j]
X[i])
(F[j]·
((¬ X[i])
(¬ ¬X[i])) );
(X[i] F[j]);
(X[i] (
F[j]));
(·) (m ( 
X[i] ) (
F[j] ) )m ) )i ) )j }.
( i ( ( (F[j]
X[i])(F[j]·equiv-rdc
=
(syn
) X[i])((¬ X[i])
(¬ ¬X[i])) );(X[i] F[j]);(X[i] (
F[j]));(m ( M
![m]
X[i] ) (M
![m]
F[j] ) )m ) )i ) )j }.2.7. Elementaire Geldige en Ongeldige afleidingen.
(a)
(Semantische equivalent-reductie; Parafrase).
(Semantische degressief-reductie; Subsumptie).
(Contradictie; Reductio ad absurdum).
Equivalent-geldigheid.
(Semantische equivalent-reductie; Parafrase).
Bijv.: { h j ( (¬F[h]
G[j]) 
(F[h]
G[j]) )j ,h }.
(b) h j ( (¬F[h]
G[j]) (F[h]
G[j]) )j ,h }.Degressief-geldigheid.
(Semantische degressief-reductie; Subsumptie).
Bijv.: { h j (F[h]
G[j]) (
k l ( (F[h] C[k])
(G[j] D[l]) )l ,k ) )j
,h }.
(c) h j (F[h]
G[j]) (degres
) (
k l ( (F[h] C[k])
(G[j] D[l]) )l ,k ) )j
,h }.Contingent-ongeldigheid.
Bijv.: { h j ( (F[h]
G[j]) (
k ( (F[h] D[k])
G[j] )k ) ( l ( F
[h] (G[j] C[l]
) )l ) ) )j ,h }.
(d) h j ( (F[h]
G[j]) (nonseq
) ( (
k ( (F[h] D[k])
G[j] )k ) ( l ( F
[h] (G[j] C[l]
) )l ) ) )j ,h }.Inconsistent-ongeldigheid.
(Contradictie; Reductio ad absurdum).
Bijv.: { h j ( (F[h]
G[j]) (
¬G[j]) )j ,h }.
h j ( (F[h]
G[j]) (contrad
) (F[h]
¬G[j]) )j ,h }.
2.8. Geldigheid, Vervulbaarheid en Contingentie.
Schema Geldigheid / Vervulbaarheid / Definiet-contingentie |
||
|---|---|---|
1 |
± |
0 |
Niet noodzakelijk onwaar:Vervulbaar,Logische mogelijkheid. (Is nog niet hetzelfde als 'mogelijk waar').
SATBL(G);
(TAUT(G) D-CONTIN(G);¬ ¬G;((G ) (¬
(¬G ) ) );{ t ( (G$ = c[t]
) (c[t] >$0) )t };{ j F[j]
G };{ m M![m]
G }.{ j ((F[j]
¬F[j]) G) }; |
Onmogelijk waar:Onvervulbaar,Logisch uitgesloten. 'Uitgesloten grond'.
¬SATBL(G);
¬G;{ t ( (G$ = c[t]
) (c[t] = $0) )t };{¬j ((¬
¬F[j]) (F[j] G
)) };{¬m M![m]
G }.{ j ((F[j]
¬F[j]) G) }; |
|
Consistentie,Widerspruchsfreiheit. Verzameling K* is consistent: Uit K* is geen contradictie afleidbaar.
CONSIS(K*);
{ ¬( (K*  G)
(K* ¬G) ) }; { ¬(K* 
) }; { j ( ¬( (K*
F[j]) (K* ¬F
[j]) )j }; { j ( ¬( {K* 
F[j]} )¬( {K* ¬F[j]}
) )j }; { ¬j ( ( F[j]
K* )( ¬F[j] K
* ) )j }. |
Inconsistentie,Inconsistent-ongeldigheid. Verzameling K* is inconsistent. Uit K* is een contradictie afleidbaar.
INCNS(K*);
¬CONSIS(K*); { (K* G)
(K* ¬G) }; { K*
}; { j ( (K*
F[j]) (K* ¬F
[j])j }; { j ( ( {K*
F[j]} )( {K* ¬F[j]}
) )j }; { j ( ( F[j]
K* )( ¬F[j] K*
) )j }. |
|
Consistentiestelling,Fundamenteel theorema (Model-existence theorem): 'Consistentie impliceert Vervulbaarheid'. (Elke deelverzameling : (Consistent Vervulbaar)).
{CONSIS(K*)
SATBL(K*)};{¬(K*
) ¬(K* 
)}. |
||
Noodzakelijk/ altijd waar:Geldig,Tautologie, Geldig-vervulbaarheid.
TAUT(G);
G;{ t ( (G$ = c[t]
) (c[t] = $1) )t };{¬j ((¬
¬F[j]) (F[j] ¬
G)) };{¬m M![m]
¬G }.{¬j (F[j]
¬F[j] G) }; |
Noch waar, noch onwaar:Definiet-contingentie,Contingent-ongeldigheid (ongeldig maar consistent), Contingent-vervulbaarheid (ongeldig maar vervulbaar),
D-CONTIN(G);
{SATBL(G) ¬TAUT(G)};{(¬ G) (¬
¬G)};{ t ( (G$ = c[t]
)($0 <c[t]<$1) )t };{ j ((¬
¬F[j]) (F[j] G
)) } { h ((¬
¬H[h]) (H[h] ¬
G)) };{ (m M![m]
G)(n M! [n] ¬G) }. |
|
Niet noodzakelijk-waar:Ongeldig.Onvoldoende grond, non sequitur [nonseq]:
NONSEQ(G);
¬TAUT(G);(D-CONTIN(G) ¬SATBL(G);¬ G;{ t ( (G$ = c[t]
) (c[t] <$1) )t };{ j ((¬
¬F[j]) (F[j] ¬
G)) };{ m M![m]
¬G }. |
||
Correctheid(Soundness in-formele-zin): 'Afleidbaar impliceert logisch gevolg'. Verzameling K* is correct. (Elke deelverzameling :(Afleidbaar Logisch gevolg)).
CORRECT(K*);
{DRVBL(K*,G) SEQUIT(K*,
G)}; { (K* G)
(K* G) }; { j ( (K*
F[j]) (K* F
[j]) ) }. |
||
Volledigheid(Completeness, Vollständigkeit). 'Waarheid/ Geldigheid impliceert Afleidbaarheid'. Verzameling K* is volledig: (Elke deelverzameling :(Waar/ Geldig Afleidbaar)).
COMPLET(K*);
{SEQUIT(K*,G) DRVBL(K*,
G)}; { (K* G)
(K* G) }; { j ( (K*
F[i]) (K* F
[j]) ) }. |
||
Maximaal consistentie:Verzameling K* is maximaal consistent: (Elke deelverzameling :(Logisch gevolg Afleidbaar)).
MAXCONS(K*);
{ CONSIS(K*) COMPLET(K*) }; { (K* G)
(K* G) }; { j ( (K*
F[j]) (K* F
[j]) )j }; { j ( CONSIS(K* \ {F[j]
})¬CONSIS(K* {F[j]
}) )j }; { j ( ( (F[j]
K*) ( {K* ¬F[j]
} ) ) ( ¬(F[j] K*) ¬( {K* F
[j]} ) ) )j };Implicaties: { j ( (F[j]
K*)||(¬F[j]K*) )
j }; |
|
|
|
(·) Volledigheid van de PPL: bewijs door Emil L. Post (1920, Introduction to a general theory of elementary propositions). (·) Volledigheid van de PDL-I: bewijs door Kurt F. Gödel (1929/1930, Über die Vollständigkeit des Logikkalküls). |
(·) Onvolledigheid van de elementaire rekenkunde (first-order theory of natural numbers volgens het logicistisch
onderzoeksprogramma, dat gebaseerd was op de klassieke logica in het Organon van Aristotelis, en was uitgewerkt in
de Grundgesetze der Arithmetik van F.L. Gottlob Frege (1893, 1903) en de Principia Mathematica van Bertrand Russell en Alfred North Whitehead,
delen I-III (1910, 1912, 1913): bewijs door Kurt Gödel (1931, Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme 1 ). |
|
2.9. Relaties tussen logische criteria van niveau II.
(1)
(Via aanname of (re)presentatie).
( Geldig Vervulbaar /Consistent
).
( Definiet-contingent Vervulbaar /Consistent
).
( Definiet-Contingent Ongeldig ).
( Onvervulbaar /Inconsistent /Contradictie
Ongeldig ).
( Onvervulbaar /Inconsistent /Contradictie
( Valid
Geldige stelling of redenering.
(Via aanname of (re)presentatie).
( Geldig Vervulbaar /Consistent
). ( Definiet-contingent Vervulbaar /Consistent
). ( Definiet-Contingent Ongeldig ). ( Onvervulbaar /Inconsistent /Contradictie
Ongeldig ). ( Onvervulbaar /Inconsistent /Contradictie #
Vervulbaar /Consistent ). ( Valid #
Invalid ).Niveau III.
Beslisbaarheid en Recursiviteit van formele systemen
Schema Beslisbaarheid en Recursiviteit |
|||
|---|---|---|---|
1 |
± |
||
Beslisbaar,Decidable: De vraag of een expressie G een definiete (waarheids)waarde heeft, is altijd te beantwoorden: De (waarheids)waarde van G is altijd afleidbaar met een eindig bewijs. |
Onbeslisbaar,Undecidable: De vraag of een expressie G een definiete (waarheids)waarde heeft, is niet altijd te beantwoorden: De (waarheids)waarde van G is niet altijd afleidbaar met een eindig bewijs. |
||
|
G is Waarheidswaardebeslisbaar:
DECIDBL(G);
{( ( G
$1) )||( ( G
$0) ) };{( (
G ) ) ||( (
¬G ) ) };Implicaties: { ( (
G ) ||( ¬G ) ) }.{ (
( G ||¬G ) ) };{ ( G ||¬G ) };{ G ||¬G } (altijd logische waarde).$1 (waarheid). |
G is Niet waarheidswaardebeslisbaar:
¬DECIDBL(G);
{ (¬ ( G
$1) )(¬ ( G
$0) ) };{ (¬ (
G ) ) (¬ (
¬G ) ) };Implicaties: { ¬ ( (
G ) ||( ¬G ) ) };{ ¬ (
( G ||¬G ) ) };{ ¬ ( G ||¬G ) };{ } (geen logische waarde);$0 (geen waarheid). |
||
G is Validiteitsbeslisbaar:{ ( (
G) ) ||( (¬
G) ) };Implicaties: { ( (
G ) ||( ¬ G ) ) };{ ( G ) ||( ¬ G ) }.{ TAUT(G) ||¬SATBL(G) } (altijd validiteit swaarde).$1 (waarheid).G is determinaat. |
G is Niet validiteitsbeslisbaar:{ (¬ (
G) ) (¬ (¬
G) ) }; Implicaties: { ¬ ( (
G ) ||( ¬ G ) ) }.{ ¬( G )
¬( ¬G ) }.{ D-CONTIN(G) } (geen validiteitswaarde).$0 (geen waarheid).G is indeterminaat. |
||
|
Recursief: Onder alle invoer is het systeem 'halting' (terminerend in eindige tijd). |
Niet-recursief:Onder sommige invoer blijft het systeem (mogelijkerwijs) oneindig 'looping'. |
||
|
RC(G);
{ RE(G) CO-RE(G) };{ ( (
G) ) ||( (¬
G) ) };Implicaties: { ( (
G) ||(¬ G) ) }. |
¬RC(G);
{ ¬RE(G) ¬CO-RE(G) }.{ (¬ (
G) ) (¬ (¬
G) ) };Implicaties: { ¬ ( (
G) ||(¬ G) ) }. |
||
Recursief |
Co-recursief |
|
|
|
Verzameling K* is Recursief opsombaar: Als K* een uitkomst heeft, dan is dat altijd aantoonbaar.
RE(K*);
{ k ( (Ks*[k]
K*)j ( (Ks*[k]
F[j])(Ks*[k]
F[j]) )j )k }. |
Complement van K* is Recursief opsombaar: Als K* geen uitkomst heeft, dan is dat altijd aantoonbaar.
CO-RE(K*);
{ k ( (Ks*[k]
K*)j ( ¬(Ks*[k]
F[j])¬(Ks*[k]
F[j]) )j )k }. |
Verzameling K* is niet Recursief opsombaar: Als K* een uitkomst heeft, dan is dat niet altijd aantoonbaar.
¬RE(K*);
{ k ( (Ks*[k]
K*)j ( (Ks*[k]
F[j])¬(Ks*[k]
F[j]) )j )k }. |
Complement van K* is niet Recursief opsombaar: Als K* geen uitkomst heeft, dan is dat niet altijd aantoonbaar.
¬CO-RE(K*);
{ k ( (Ks*[k]
K*)j ( ¬(Ks*[k]
F[j])¬¬(Ks*[k]
F[j]) )j )k }. |
|
Verzameling K* is Recursief opsombaar (via Turing Machine procedure): Als K* een uitkomst heeft, dan is dat altijd berekenbaar.
RE(K*)TM;
{ k ( (Ks*[k]
K*)j h ((TM[h](Ks*[k]) F[j])m (TM[m](K*
) (TM[h](Ks*[k]) F
[j]) )m )h ,j )k }. |
Complement van K* is Recursief opsombaar (via Turing Machine procedure): Als K* geen uitkomst heeft, dan is dat altijd berekenbaar.
CO-RE(K*)TM;
{ k ( (Ks*[k]
K*)j h (¬(TM[h](Ks*[k]) F[j])m ( (TM[m](K*
) ¬(TM[h](Ks*[k]) F
[j]) )m )h ,j )k }. |
Verzameling K* is niet Recursief opsombaar (via Turing Machine procedure): Als K* een uitkomst heeft, dan is dat niet altijd berekenbaar.
¬RE(K*)TM;
{ k ( (Ks*[k]
K*)j h ((TM[h](Ks*[k]) F[j])¬m (TM[m](K*
) (TM[h](Ks*[k]) F
[j]) )m )h ,j )k }. |
Complement van K* is niet Recursief opsombaar (via Turing Machine procedure): Als K* geen uitkomst heeft, dan is dat niet altijd berekenbaar.
¬CO-RE(K*)TM;
{ k ( (Ks*[k]
K*)j h (¬(TM[h](Ks*[k]) F[j])¬m (TM[m](K*
) ¬(TM[h](Ks*[k]) F
[j]) )m )h ,j )k }. |
|
(·) 'Effective procedure' (Hilbert, 1900, 1928). (·) 'Recursive function' (Gödel, 1930, 1931). (·) 'Lambda definable function' (Church, 1935, 1936). (·) 'Turing Machine computable function' (Turing, 1936, 1937). |
(·) Onbeslisbaarheid/ niet-recursiviteit van de elementaire calculus van natuurlijke getallen (elementary number theory): bewijs door Alonzo Church, (1935/1936, An Unsolvable Problem of Elementary Number Theory). (·) Onbeslisbaarheid/ niet-recursiviteit van de gehele elementaire rekenkunde (first order arithmetic): bewijs door Alan M. Turing (1936/1937, On computable numbers, with an application to the Entscheidungsproblem). |
||
4. Tabel met Enkele Mijlpalen in de Meta-logica
| Auteur | Jaar | Formalisme | Domein | Criterium | |
|---|---|---|---|---|---|
| Hilbert | 1900,1928 | Effectieve procedure (hypothetisch) | Wiskunde, Logica |
Decidability; Entscheidbarheit; Entscheidungs-definitheit; Beslisbaarheid. |
|
| Post | 1920 |
Truth table method |
PPL |
Completeness; Vollständigkeit; Volledigheid. |
|
| Gödel | 1929/1930 | Deduction | PDL-I |
Completeness; Vollständigkeit; Volledigheid. Recursief opsombaar (Recursively enumerable) |
|
| Gödel | 1931 | Gödel-nummering |
PDL-I, Rekenkunde van Natuurlijke getallen First-order theory of natural numbers (Principia Mathematica) |
Einige formal unentscheidbare Satze: Unvollständigkeit; Onvolledigheid. Niet-Recursief opsombaar (Not recursively enumerable). |
|
| Church | 1935/1936 |
Lambda-calculus (Lambda-definable): Recursive functions of positive integers |
PDL-I, Rekenkunde Natuurlijke getallen: Elementary number theory |
Unsolvable problem: Undecidability; Unentscheidbarheit; Onbeslisbaarheid. |
|
| Turing | 1936/1937 |
(Universal) Turing machine (Turing machine computability) |
PDL-I, Rekenkunde: First order arithmetic |
Undecidability; Unentscheidbarheit; Onbeslisbaarheid |
5. Criteria in de formele logica
In het overzicht ' Criteria in de Formele Logica' worden de belangrijkste criteria in de formele logica besproken.
Deze criteria zijn van toepassing op formules, zinnen, verzamelingen, theorieën en (taal)systemen in de logica.
Ze dienen om volkomen exact de meest essentiële eigenschappen van bepaalde gegevens weer te geven: de kwaliteit, de rijkweidte, de mogelijkheden maar ook de beperkingen.
Criteria in de Formele Logica
(1)
Criteria voor beslissingen over inhoudelijke aspecten van taaluitingen.
O.a. vervulbaarheid, geldigheid, (definiet-)contingentie, eindig-vervulbaarheid, compactheid, etc..
(2)
Criteria voor beslissingen over aspecten van vorm en ordening van beweringen.
Correctheid: O.a. afleidbaarheid, bewijsbaarheid, consistentie.
(3)
D.w.z. projecties vanuit semantiek naar syntax.
O.a. volledigheid.
(4)
D.w.z. projecties vanuit syntax naar semantiek.
O.a. consistentiestelling, correctheid, Beslisbaarheid.
Semantische criteria
Criteria voor beslissingen over inhoudelijke aspecten van taaluitingen.
O.a. vervulbaarheid, geldigheid, (definiet-)contingentie, eindig-vervulbaarheid, compactheid, etc..
(1a) Vervulbaarheid (satisfiability): Waarheid onder minstens één mogelijke interpretatie.
((Welgevormd niet-Weerlegd)
Vervulbaar).
(1b) Geldigheid (validiteit, tautologie): Waarheid onder èlke mogelijke interpretatie.
((Welgevormd altijd-Waar)
Geldig).
(1c) Definiet-Contingentie: Vervulbaar, maar niet geldig.
(Waar onder minstens één mogelijke interpretatie, maar niet elke).
((Welgevormd (Vervulbaar
niet-Geldig)) Definiet-contingent).
(1d) Eindig-vervulbaarheid (finitely satisfiability): Een (deel)verzameling van formules is eindig en vervulbaar.
(((Deel)verzameling: (Welgevormd (Eindig
Vervulbaar))) Eindig-vervulbaar).
(1e) Compactheid: Als elke eíndige deelverzameling (subset) van een - mogelijk oneindige - verzameling vervulbaar
is, dan is die verzameling als geheel vervulbaar.
(((Elke deelverzameling: (Welgevormd Eindig-vervulbaar
)) Vervulbaar) Compact).
((Welgevormd niet-Weerlegd)
Vervulbaar).((Welgevormd altijd-Waar)
Geldig).(Waar onder minstens één mogelijke interpretatie, maar niet elke).
((Welgevormd (Vervulbaar
niet-Geldig)) Definiet-contingent).(((Deel)verzameling: (Welgevormd (Eindig
Vervulbaar))) Eindig-vervulbaar).(((Elke deelverzameling: (Welgevormd Eindig-vervulbaar
)) Vervulbaar) Compact).(2)
Syntactische criteria.
Criteria voor beslissingen over aspecten van vorm en ordening van beweringen.
Correctheid: O.a. afleidbaarheid, bewijsbaarheid, consistentie.
(2a) Afleidbaarheid: Afleidbaar via syntactische productieregels.
((Welgevormd resultaat van uitsluitend correcte formele bewerkingen)
Afleidbaar).
(2b) Bewijsbaarheid (eindig-afleidbaarheid): Syntactisch afleidbaar via een eindige afleidingsreeks.
(((Welgevormd resultaat van eindige reeks louter formele bewerkingen)
Eindig-afleidbaar) Bewijsbaar).
(2c) Consistentie: Afleidbaar garandeert non-contradictie.
(Voor elke deelverzameling: ((Afleidbaar Non-contradictie)
Consistent)).
(2d) Maximaal consistentie: Consistentie garandeert inconsistentie bij elke mogelijke semantische (d.i. niet-redundante, conjuncte)
uitbreiding.
((Consistent (toevoeging van elke andere formule
inconsistent)) Maximaal-consistent).
(2e) Negatie-volledigheid (negation-completeness): Verzameling K* bevat voor elke welgevormde zin in de taal
hetzij de bevesting, hetzij de ontkenning.
((Elke deelverzameling: (Welgevormd (Waarheidsbeslissing
(hetzij Waar, hetzij Onwaar)))) Negatie-volledig
).
((Welgevormd resultaat van uitsluitend correcte formele bewerkingen)
Afleidbaar).(((Welgevormd resultaat van eindige reeks louter formele bewerkingen)
Eindig-afleidbaar) Bewijsbaar).(Voor elke deelverzameling: ((Afleidbaar Non-contradictie)
Consistent)).((Consistent (toevoeging van elke andere formule
inconsistent)) Maximaal-consistent).((Elke deelverzameling: (Welgevormd (Waarheidsbeslissing
(hetzij Waar, hetzij Onwaar)))) Negatie-volledig
).(3)
Semantische criteria, m.b.t. syntax:
D.w.z. projecties vanuit semantiek naar syntax.
O.a. volledigheid.
(3a) Syntactisch - Adequatie.
Vervulbaarheid garandeert Consistentie.
((Elke deelverzameling: (Vervulbaar Consistent))
Adequaat).
(3b) Syntactisch - Volledigheid (bewijskracht, Completeness, Vollständigkeit).
Waarheid/ Geldigheid garandeert Afleidbaarheid.
((Elke deelverzameling: (Waar/ Geldig Afleidbaar))
Volledig).
Vervulbaarheid garandeert Consistentie.
((Elke deelverzameling: (Vervulbaar Consistent))
Adequaat).Waarheid/ Geldigheid garandeert Afleidbaarheid.
((Elke deelverzameling: (Waar/ Geldig Afleidbaar))
Volledig).(4)
Syntactische criteria, m.b.t. semantiek:
D.w.z. projecties vanuit syntax naar semantiek.
O.a. consistentiestelling, correctheid, Beslisbaarheid.
(4a) Fundamenteel theorema, consistentiestelling (Model-existence theorem):
Consistentie garandeert vervulbaarheid.
((Elke deelverzameling: (Consistent Vervulbaar))
Fundamenteel theorema).
(4b) Logische correctheid van formele systemen ('soundness', in zwakke betekenis, deductieve kracht):
Afleidbaarheid garandeert Waarheid/ Geldigheid.
((Elke deelverzameling: (Afleidbaar Waar/ Geldig))
Correct).
(4c) Logische 'soundness' van formele systemen, (in sterke betekenis): Afleidbaarheid garandeert Logisch Gevolg
.
((Elke deelverzameling: (Afleidbaar Logisch gevolg))
Sound).
(4d) Reductio ad absurdum: Logische geldigheid garandeert Non-contradictie.
((Welgevormd (Tegendeel/Ontkenning
(Een conjuncte deelverzameling: (Contradictie afleidbaar: inconsistent)))) Waar/ Geldig).
(4e) Beslisbaarheid (besliscapaciteit) van formele systemen: Syntactische welgevormdheid garandeert
validiteitsbeslissing.
((Welgevormd (Geldigheidsbeslissing:
(hetzij Geldig, hetzij Ongeldig))) ValiditeitsBeslisbaar).
Consistentie garandeert vervulbaarheid.
((Elke deelverzameling: (Consistent Vervulbaar))
Fundamenteel theorema).((Elke deelverzameling: (Afleidbaar Waar/ Geldig))
Correct).((Elke deelverzameling: (Afleidbaar Logisch gevolg))
Sound).
Dus uit bewijsbaarheid van contradictie afgeleid uit het tegendeel, volgt logische geldigheid.
Principe van bewijs door 'weerlegging van het tegendeel'.
Principe van bewijs door 'weerlegging van het tegendeel'.
((Welgevormd (Tegendeel/Ontkenning
(Een conjuncte deelverzameling: (Contradictie afleidbaar: inconsistent)))) Waar/ Geldig).
((Welgevormd (Geldigheidsbeslissing:
(hetzij Geldig, hetzij Ongeldig))) ValiditeitsBeslisbaar).C.P. van der Velde © 2006, 2018.