Method of 'Formal Logic'
Diagrams
Logical levels and criteria
Contents
1. Level I: Truth / Falsity of statements
2. Level II: Satisfiability / validity
2.1. Truth-values table for PPL - bivalid, for two variables.
2.2. Truth-values table for PDL - bivalid, for two variables.
2.3. Truth / validity and logical power.
2.4. Formulas in standarized vorm.
2.5. Judging theories. (sets of propositions).
2.6. Contingency and Presupposition.
2.7. Basic Valid and Invalid derivations.
2.8. Validity, Satisfiability and Contingency.
2.9. Relations between logical criteria of level II.
2.2. Truth-values table for PDL - bivalid, for two variables.
2.3. Truth / validity and logical power.
2.4. Formulas in standarized vorm.
2.5. Judging theories. (sets of propositions).
2.6. Contingency and Presupposition.
2.7. Basic Valid and Invalid derivations.
2.8. Validity, Satisfiability and Contingency.
2.9. Relations between logical criteria of level II.
4. Table with some Milestones in Meta-logic
5. Criteria in formal logic
Meta-truth: logical criteria
Logical quality |
|---|
Level I:
Truth / Falsity
of statements
1.1. Truth-values table for PPL for two variables.
In a formal logical system all possible logical relations are completely defined by a chosen vocabulary by means of a Truth values-table.
The Truth-values table for the most simple logical system, propositional logic (PPL), covers - for any chosen formalism or format - in any way all basic combinations that are involved in the most elementary beginning of any form of reasoning. Because of this, it really provides the very first, necessary foundings of accurate combinatory thinking.
Truth-values table PPL - for one variable.
This Truth-values table contains all possible orderings of values of two variables (propositions) in PPL, than can adopt two values.
The basis consists of one variable by two values = two basic combinations. With this, two orders are possible of series of truth values: each of which reflects a unique logical relation. Thus the following table arises of the most simple nature, of two rows by two columns is four cells.
Table 1.
| 1 | 2 |
|---|---|
| 1 | 0 |
| 0 | 1 |
| T | F |
| A | ¬A |
| ¬B | B |
Table 2.
Truth values |
||
|---|---|---|
1 |
± |
0 |
True,verum: Verification. |
Unspecified,uninterpreted: Indefinite. |
False,falsum: Falsification. |
Truth value(value, valor): |
||
$(G)=1. |
(0 <$(G)<1). |
$(G)=0. |
Truth value assignment(valuation): |
||
|
V!(G) :=1. |
¬V!(G)  {0,1}. {0,1}. |
V!(G) :=0. |
Truth value determination(evaluation), through a finite proof: |
||
 i E![i] i E![i]  G. G. |
(¬ i E![i] i E![i]  G) G)
 (¬ (¬ j E![j] j E![j]
 ¬G). ¬G). |
 i E![i] i E![i]  ¬G. ¬G. |
Interpretation(denotation, assignment): |
||
 m m M![m] G
. G
. |
(¬ m m M![m] G
) G
)  (¬ (¬ n n M![n] ¬G). ¬G). |
 m m M![m] ¬G
. ¬G
. |
Neither true nor false:
x!--[
Undecided:
]--x
D-CONTIN(G);
 {SATBL(G)
{SATBL(G)  ¬TAUT(G)};
¬TAUT(G)};
 {(¬
{(¬ G)
G)
 (¬
(¬ ¬G)};
¬G)};
 {
{  k ( (G$ =
c[k])
k ( (G$ =
c[k])
 ($0
($0
 {
{  j ((¬
j ((¬
 ¬F[j])
¬F[j])  (F[j]
(F[j]
 G)) }
G)) }
 {
{  k ((¬
k ((¬
 ¬F[k])
¬F[k])  (F[k]
(F[k]
 ¬G)) };
¬G)) };
 { (
{ ( m
m  G)
G)
 (
( n
n  ¬G) }.
¬G) }.
 {SATBL(G)
{SATBL(G)  ¬TAUT(G)};
¬TAUT(G)}; {(¬
{(¬ G)
G)
 (¬
(¬ ¬G)};
¬G)}; {
{  k ( (G$ =
c[k])
k ( (G$ =
c[k]) ($0
($0 <
c[k]<
$
1) )k }; {
{  j ((¬
j ((¬
 ¬F[j])
¬F[j])  (F[j]
(F[j]
 G)) }
G)) }  {
{  k ((¬
k ((¬
 ¬F[k])
¬F[k])  (F[k]
(F[k]
 ¬G)) };
¬G)) }; { (
{ ( m
m M
![ m] G)
G) (
( n
n M
![n] ¬G) }.
¬G) }.Level II:
Satisfiability / validity
2.1. Truth-values table for PPL - bivalid.
This truth-values table contains all possible ordenings of values under the combination of two variables that each can adopt two values.
Its base consists of 2 values to the power of 2 variables = 4 basic combinations or (possible) domain states .
With this, 2 to the power of 4 = 16 orders are possible of series of truth values.
Each of these reflects a unique logical relation, or (possible) domain states-relation.
Thus the following table arises of 4 columns by 16 rows is 64 cells; each containing one precise truth value .
Table 3.
Table bivalid value combinations |
||||||||
|---|---|---|---|---|---|---|---|---|
| No. | Value pattern |
Logical relation in PPL |
Logical power | |||||
| 1 | 1 | 1 | 1 | 1 |
T |
¬F |
X ¬ ¬X |
0 |
| 2 | 0 | 0 | 0 | 0 |
F |
¬T |
X ¬ ¬X |
1 |
| 3 | 1 | 1 | 0 | 0 |
A |
¬¬A |
0.50 | |
| 4 | 1 | 0 | 1 | 0 |
B |
¬¬B |
0.50 | |
| 5 | 0 | 0 | 1 | 1 |
¬A |
¬A |
0.50 | |
| 6 | 0 | 1 | 0 | 1 |
¬B |
¬B |
0.50 | |
| 7 | 1 | 0 | 0 | 0 |
A B |
¬(¬A ¬ ¬B) |
0.75 | |
| 8 | 0 | 1 | 0 | 0 |
A ¬ ¬B |
¬(¬A B) |
0.75 | |
| 9 | 0 | 0 | 1 | 0 |
¬A B |
¬(A ¬ ¬B) |
0.75 | |
| 10 | 0 | 0 | 0 | 1 |
¬A ¬ ¬B |
¬(A B) |
A\B |
0.75 |
| 11 | 1 | 1 | 1 | 0 |
A B |
¬(¬A ¬ ¬B) |
0.25 | |
| 12 | 1 | 1 | 0 | 1 |
A ¬ ¬B |
¬(¬A B) |
A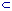 B |
0.25 |
| 13 | 1 | 0 | 1 | 1 |
¬A B |
¬(A ¬ ¬B) |
A B |
0.25 |
| 14 | 0 | 1 | 1 | 1 |
¬A ¬ ¬B |
¬(A B) |
A|B |
0.25 |
| 15 | 1 | 0 | 0 | 1 |
A B |
¬(A#B) |
0.50 | |
| 16 | 0 | 1 | 1 | 0 |
A#B |
¬(A B) |
0.50 | |
|
{Courtesy: Benjamin Peirce (1809-1880), Friedrich Wilheml Karl Ernst Schröder (1841-1902), e.a..} |
||||||||
|
{Cf.: Proof method for Propositional logic: the Truth-value
table method.} |
||||||||
2.2. Truth-values table for PDL - bivalid .
In predicate logic (PDL) attributes (or predicates) may be applied to various domain elements.
Because of this, the combinatory possibilities again increase in hyper-exponential ways.
Next, in PDL so-called quantors may be applied to predications on object-variables, to represent systematic relations between predications with identical predicate names, on identical variable names in a concise manner (conjunctive relations through universal quantors, disjunctive relations through existential quantor). However, before we succeed in finding these regularities, we still have tot deal with that combinatory explosion.
Following here is a simple example: for a bivalid system, of a 'tiny' size: consisting of one predicate, of arity one, and a domain of only two elements. With this we end up again with 16 possible logical relations.
Table 4.
Table bivalid value combinations |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Value pattern |
Logical relation in PPL |
Logical relation in PDL |
Logical relation in Skolem L. |
Logical power | ||||||
| 1 | 1 | 1 | 1 | 1 |
T |
¬F |
X ¬ ¬X |
0 | |||
| 2 | 0 | 0 | 0 | 0 |
F |
¬T |
X ¬ ¬X |
1 | |||
| 3 | 1 | 1 | 0 | 0 |
A1 |
¬¬A1 |
0.50 | ||||
| 4 | 1 | 0 | 1 | 0 |
A2 |
¬¬A2 |
0.50 | ||||
| 5 | 0 | 0 | 1 | 1 |
¬A1 |
¬A1 |
0.50 | ||||
| 6 | 0 | 1 | 0 | 1 |
¬A2 |
¬A2 |
0.50 | ||||
| 7 | 1 | 0 | 0 | 0 |
A1 A2 |
¬(¬A1 ¬ ¬A2) |
 x x A[x] |
¬ x ¬ x ¬A[x] |
A[x] |
0.75 | |
| 8 | 0 | 1 | 0 | 0 |
A1 ¬ ¬A2 |
¬(¬A1 A2) |
0.75 | ||||
| 9 | 0 | 0 | 1 | 0 |
¬A1 A2 |
¬(A1 ¬ ¬A2) |
0.75 | ||||
| 10 | 0 | 0 | 0 | 1 |
¬A1 ¬ ¬A2 |
¬(A1 A2) |
A1\A2 |
¬ x x A[x] |
 x ¬ x ¬A[x] |
¬A[x] |
0.75 |
| 11 | 1 | 1 | 1 | 0 |
A1 A2 |
¬(¬A1 ¬ ¬A2) |
 x x A[x] |
¬ x ¬ x ¬A[x] |
A[cs] |
0.25 | |
| 12 | 1 | 1 | 0 | 1 |
A1 ¬ ¬A2 |
¬(¬A1 A2) |
A1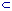 A2 |
0.25 | |||
| 13 | 1 | 0 | 1 | 1 |
¬A1 A2 |
¬(A1 ¬ ¬A2) |
A1 A2 |
0.25 | |||
| 14 | 0 | 1 | 1 | 1 |
¬A1 ¬ ¬A2 |
¬(A1 A2) |
A1|A2 |
¬ x x A[x] |
 x ¬ x ¬A[x] |
¬A[cs] |
0.25 |
| 15 | 1 | 0 | 0 | 1 |
A1 A2 |
¬(A1#A2) |
(A1 A2) (¬ (¬A1 ¬ ¬A2) |
0.50 | |||
| 16 | 0 | 1 | 1 | 0 |
A1#A2 |
¬(A1 A2) |
(A1 ¬ ¬A2) (¬ (¬A1 A2) | 0.50 | |||
2.3. Truth value and logical power.
Logical power is inversely proportional to truth value.
Given a formula F - that is a each possible logical relation under formal system
L!
- of set T* (with size t=
v**(v**d)). The following applies:
(a)
F is derivable from the maximum logical power in
 {
{  j ( (F[j]
j ( (F[j]
 T*)
T*)  ($0
($0
 F[j]) )j;
F[j]) )j;

 j ($0
j ($0  F[j]) j;
F[j]) j;
 ($0
($0  (
(  j
j
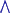 F[j]) );
F[j]) );
 ($0
($0  (
(  j
F[j]) );
j
F[j]) );
 ($0
($0  (
(  j
j
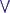 F[j]) );
F[j]) );
 ($0
($0  (
( T
*)) }.
T
*)) }.
(b)
F serves to derive the minimum logical power in
 {
{  j ( (F[j]
j ( (F[j]
 T*)
T*)  (F[j]
(F[j]


 j (F[j]
j (F[j]

 ((
((  j
j  F[j])
F[j]) 
 ((
((  j
j 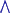 F[j])
F[j]) 
 ((
(( j F[j])
j F[j])

 ((
(( T*)
T*)

(c)
Combining (a) and (b).
 {
{  j ( (F[j]
j ( (F[j]
 T*)
T*)  ( ($0
( ($0
 F[j])
F[j])  (F[j]
(F[j]


 j ( ($0
j ( ($0  F[j])
F[j])  (F[j]
(F[j]

 ( ($0
( ($0  (
( j
j
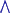 F[j]) )
F[j]) )  ( (
( (
 j
j 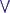 F[j])
F[j])

 ( ($0
( ($0  (
( j
j
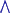 F[j]) )
F[j]) )  ( (
( (
 j
j 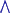 F[j])
F[j])

 ( ($0
( ($0  (
( j
F[j]) )
j
F[j]) )  ( (
( ( j F
[j])
j F
[j]) 
 ( ($0
( ($0  (
( j
j
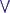 F[j]) )
F[j]) )  ( (
( (
 j
j 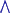 F[j])
F[j])

 ( ($0
( ($0  (
( T
*))
T
*))  ( (
( ( T*)
T*)

 ($0
($0 
In formal logic a set of logical formulas is called a theory. The formulas in the set in general refer to statements or arguments (propositions).
In formal logic a number of standarized forms exists by which formulas or sets of formulas can be represented in a clear, precise and compact manner, so that they can be processed and be judged efficiently, so-called normal forms. ]-->
A convenient form for formulas when we want to judge them is the Conjunctive Normal Form (
A ,
,
 }.
}.
General structure of a
 { (T*
{ (T*
 (
(  k ( (K*[k]
k ( (K*[k]
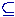
 (K*[k]
(K*[k]  [ F[2]
[ F[2]  .. ] ] F
[n[k]] } )
.. ] ] F
[n[k]] } )
 (n[k]
(n[k]
 (K*[k]
(K*[k] 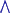 (j[k]=1,..n[k]) F[j[k]] } )
(j[k]=1,..n[k]) F[j[k]] } )
 ( (
( (  j ( (F[j]
j ( (F[j]
 K*[k])
K*[k])
 F[j]
F[j]  [ G[j,2]
[ G[j,2]  .. G
[m[j[k]]] ] ] } )
.. G
[m[j[k]]] ] ] } )
 (m[j[k]]
(m[j[k]]
 ( (F[j]
( (F[j] 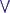 (h[j[k]]=1,..h[n[k]]) G[h[j[k]]]) } )
(h[j[k]]=1,..h[n[k]]) G[h[j[k]]]) } )
 ( (0
( (0  (0
(0
How can we judge the logical 'status', or semantical value, of such a set? This is dependent of the formal system, or the logical language in which the set has been formulated.
We can only mention some preconditions that in general apply to judge a set of formulas.
In its most general sense, 'contingent' means indefinite, which meaning can in turn have various shades: not defined, not yet established, conditional, thus yet to be determined; also: not necessarily (the case), not inherent, not essential; sometimes also: accidental, 'by chance' or subject to chance, coincidence and the like.
In formal logic we can distinguish two meanings of the term contingency which can be defined in a perfectly precise and exact way.
To be distinguished:
A formula F[j] is definitely-contingent:
 {
{  j ( D-CONTIN(F[j] );
j ( D-CONTIN(F[j] );

Table 5.
Logical power and contradiction.
F is derivable from the maximum logical power in
L!
: i.e. contradiction (falsity under all conditions); or falsity; or truth value$
0. {
{  j ( (F[j]
j ( (F[j]
 T*)
T*)  ($0
($0
 F[j]) )j;
F[j]) )j;
 j ($0
j ($0  F[j]) j;
F[j]) j; ($0
($0  (
(  j
j
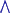 F[j]) );
F[j]) ); ($0
($0  (
(  j
F[j]) );
j
F[j]) ); ($0
($0  (
(  j
j
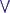 F[j]) );
F[j]) ); ($0
($0  (
( T
*)) }.
T
*)) }.Logical power and truth.
F serves to derive the minimum logical power in
L!
: i.e. validity (truth under all conditions); or truth; or truth value$
1. {
{  j ( (F[j]
j ( (F[j]
 T*)
T*)  (F[j]
(F[j]

$
1) )j;
 j (F[j]
j (F[j]

$
1) j; ((
((  j
j 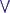 F[j])
F[j]) 
$
1 ); ((
((  j
j 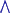 F[j])
F[j]) 
$
1 ); ((
(( j F[j])
j F[j])

$
1 ); ((
(( T*)
T*)

$
1 ) }.Contradiction, Logical power and truth.
Combining (a) and (b).
 {
{  j ( (F[j]
j ( (F[j]
 T*)
T*)  ( ($0
( ($0
 F[j])
F[j])  (F[j]
(F[j]

$
1) ) )j;
 j ( ($0
j ( ($0  F[j])
F[j])  (F[j]
(F[j]

$
1 ) )j; ( ($0
( ($0  (
( j
j
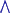 F[j]) )
F[j]) )  ( (
( (
 j
j 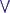 F[j])
F[j])

$
1 ) ); ( ($0
( ($0  (
( j
j
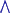 F[j]) )
F[j]) )  ( (
( (
 j
j 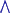 F[j])
F[j])

$
1 ) ); ( ($0
( ($0  (
( j
F[j]) )
j
F[j]) )  ( (
( ( j F
[j])
j F
[j]) 
$
1 ) ); ( ($0
( ($0  (
( j
j
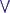 F[j]) )
F[j]) )  ( (
( (
 j
j  F[j])
F[j])

$
1 ) ); ( ($0
( ($0  (
( T
*))
T
*))  ( (
( ( T*)
T*)

$
1) ); ($0
($0 
$
1) }.2.4. Formulas in standarized vorm.
In formal logic a set of logical formulas is called a theory. The formulas in the set in general refer to statements or arguments (propositions).
In formal logic a number of standarized forms exists by which formulas or sets of formulas can be represented in a clear, precise and compact manner, so that they can be processed and be judged efficiently, so-called normal forms. ]-->
A convenient form for formulas when we want to judge them is the Conjunctive Normal Form (
CNF
). A formula inCNF
consists of a conjunction of disjunctions. In other words, on the mainline of argumentation a juxtaposition of one or more conjuncts exists, while each conjunct is a disjunction consisting of at least one simple formula (an atom or a literal).A
CNF
thus makes only use of the connectives {¬, ,
,
 }.
}.General structure of a CNF
set:
 { (T*
{ (T* =
WFF*(L!
PDl )); (
(  k ( (K*[k]
k ( (K*[k]
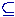
CNF
*(T*)) (K*[k]
(K*[k] =
{ [ F[1] [ F[2]
[ F[2]  .. ] ] F
[n[k]] } )
.. ] ] F
[n[k]] } ) (n[k]
(n[k] =
|
K*[k]|
) (K*[k]
(K*[k] =
{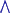 (j[k]=1,..n[k]) F[j[k]] } )
(j[k]=1,..n[k]) F[j[k]] } ) ( (
( (  j ( (F[j]
j ( (F[j]
 K*[k])
K*[k]) F[j]
F[j] =
{ [ G[j,1] [ G[j,2]
[ G[j,2]  .. G
[m[j[k]]] ] ] } )
.. G
[m[j[k]]] ] ] } ) (m[j[k]]
(m[j[k]] =
|
F[j]|
 ( (F[j]
( (F[j] =
{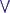 (h[j[k]]=1,..h[n[k]]) G[h[j[k]]]) } )
(h[j[k]]=1,..h[n[k]]) G[h[j[k]]]) } ) ( (0
( (0 >
j[k]≥
n[k] ) (0
(0 >
h[j[k]]≥
m[j[k]]) ) ) ) j )k ) }.2.5. Judging theories (sets of propositions).
How can we judge the logical 'status', or semantical value, of such a set? This is dependent of the formal system, or the logical language in which the set has been formulated.
We can only mention some preconditions that in general apply to judge a set of formulas.
General requirements for judging a theory :
(a)
 {
{  k ( (K*[k]
k ( (K*[k]
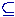
 ( (
( (  j ( (F[j]
j ( (F[j]
 K*[k])
K*[k])
 ( (F[j]
( (F[j]
 ( (
( ( (
(  h ( (G[h[j[k
]]]
h ( (G[h[j[k
]]]  F[j])
F[j])  (G
[h[j[k]]]
(G
[h[j[k]]]
)  (K*[k]
(K*[k]
(b)
 {
{  k ( (K*[k]
k ( (K*[k]
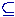
 ( (
( (  j ( (F[j]
j ( (F[j]
 K*[k])
K*[k])
 ( (F[j]
( (F[j]
 ( (
( ( (
(  h ( (G[h[j[k
]]]
h ( (G[h[j[k
]]]  F[j])
F[j])  (G
[h[j[k]]]
(G
[h[j[k]]]
)  (K*[k]
(K*[k]
(c)
Neither (a) nor (b).
The set is valid (is a tautology).
 {
{  k ( (K*[k]
k ( (K*[k]
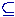
CNF
*(T*)) ( (
( (  j ( (F[j]
j ( (F[j]
 K*[k])
K*[k]) ( (F[j]
( (F[j]$
=
1) ( (
( (|
F[j]|
>
1) (
(  h ( (G[h[j[k
]]]
h ( (G[h[j[k
]]]  F[j])
F[j])  (G
[h[j[k]]]
(G
[h[j[k]]]$
=
1) )h ) ) ) )j ) (K*[k]
(K*[k]$
=
1) ) k }.(b)
The set is inconsistent (contains contradiction).
 {
{  k ( (K*[k]
k ( (K*[k]
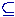
CNF
*(T*)) ( (
( (  j ( (F[j]
j ( (F[j]
 K*[k])
K*[k]) ( (F[j]
( (F[j]$
=
0) ( (
( (|
F[j]|
>
1) (
(  h ( (G[h[j[k
]]]
h ( (G[h[j[k
]]]  F[j])
F[j])  (G
[h[j[k]]]
(G
[h[j[k]]]$
=
0) )h ) ) ) )j ) (K*[k]
(K*[k]$
=
0) )k }.(c)
The set is contingent (is undecided).
Neither (a) nor (b).
2.6. Contingency and Presupposition.
Contingency.
In its most general sense, 'contingent' means indefinite, which meaning can in turn have various shades: not defined, not yet established, conditional, thus yet to be determined; also: not necessarily (the case), not inherent, not essential; sometimes also: accidental, 'by chance' or subject to chance, coincidence and the like.
In formal logic we can distinguish two meanings of the term contingency which can be defined in a perfectly precise and exact way.
(1)
Contingent in the sense of sub-specific indefinite, or indefinitely. Which means: (entirely) undecided as for the truth value.
(Not to be confused with indefinite in mathematic, algebraic sense).
The truth value can therefore in principle still vary 'freely' over the entire value scale, that is in a binary system from 0[00..] (false, contradiction) to 1[11..] (true, valid, tautology), i.e. both these extremes included.
 {
{  j (I-CONTIN(F[j] )
j (I-CONTIN(F[j] )
 ((0[00..) ≤
((0[00..) ≤
 (
(
A statement or reasoning which is indefinitely-contingent, is thus not (yet) valuated.
Therefore, it does not necessarily need to be (finitely-)provable.
It doesn't even have to be decidable.
So it has not been validated, So it doesn't have to be valid too.
It certainly doesn't have to consistent.
(2)
Contingent in the sense of specifically indefinite, or definite, which means (entirely) decided as for the truth value.
The truth value however, is here between the extreme values of the value scale, that is in a binary system as it were 'locked in' between 0[00..] (false, contradiction) to 1[11..] (true, valid, tautology), i.e. both these extremes excluded.
 {
{  j (D-CONTIN(F[j] )
j (D-CONTIN(F[j] )
 ((0[00..) <
((0[00..) <
 (
(
A statement or reasoning which is definitely-contingent, has therefore been shown to be
- in terms of truth/validity - not (finitely-)provable.
As such, she has thus been shown to be decidable.
She is indeed thereby proven to be invalid, and in addition, she has proven to be consistent, and, moreover, according to the Consistency Theorem (see 2.8) to be satisfyable.
Unless otherwise stated, 'contingent' will be used here in the sense of 'definitely-contingent' or '
contingent-invalid'.Indefinitely-contingent.
Contingent in the sense of sub-specific indefinite, or indefinitely. Which means: (entirely) undecided as for the truth value.
(Not to be confused with indefinite in mathematic, algebraic sense).
The truth value can therefore in principle still vary 'freely' over the entire value scale, that is in a binary system from 0[00..] (false, contradiction) to 1[11..] (true, valid, tautology), i.e. both these extremes included.
 {
{  j (I-CONTIN(F[j] )
j (I-CONTIN(F[j] ) ((0[00..) ≤
((0[00..) ≤ $
(F[j]) ≤ (1[11..]) ); (
($
(F[j])
[
0[00..] .. 1[11..]]
) }.It doesn't even have to be decidable.
So it has not been validated, So it doesn't have to be valid too.
It certainly doesn't have to consistent.
(2)
Definite-contingent, or Contingent-invalid.
Contingent in the sense of specifically indefinite, or definite, which means (entirely) decided as for the truth value.
The truth value however, is here between the extreme values of the value scale, that is in a binary system as it were 'locked in' between 0[00..] (false, contradiction) to 1[11..] (true, valid, tautology), i.e. both these extremes excluded.
 {
{  j (D-CONTIN(F[j] )
j (D-CONTIN(F[j] ) ((0[00..) <
((0[00..) < $
(F[j]) < (1[11..]) ); (
($
(F[j])
<
0[00..] .. 1[11..]>
) }.As such, she has thus been shown to be decidable.
She is indeed thereby proven to be invalid, and in addition, she has proven to be consistent, and, moreover, according to the Consistency Theorem (see 2.8) to be satisfyable.
Presupposition.
To be distinguished:
(1) Logical presupposition is what completes the grounds of an invalid inference pattern
thus making the latter valid.
She is only bounded to universal abstract patterns following laws and principles of a system of (formal, or combinatory) logic.
(2) Linguistic presupposition is different: namely, what is implied by a language expression or sign-giving regardless of any truth value of the latter in her references (is as it where a consequens in termines).
She is bounded to specific language symbols and structures following conventional rules of syntax and lexicon of a (human) language system.
Both are therefore not directly physically-bound (i.e. not to time, space, energy, matter).
(3) A prejudice is an internal, mental or psychological content, in particular of cognitive nature.
Thus she is bounded to a person or group (performative, author, source). Because of this, she is at least in part, and at least first - through neuro-physiology - physically-bound. Thus she is essentially incidental of nature (although possibly of relative long duration). She precedes in time actual conclusions, decisions, utterances, behavior, etc..
She is only bounded to universal abstract patterns following laws and principles of a system of (formal, or combinatory) logic.
(2) Linguistic presupposition is different: namely, what is implied by a language expression or sign-giving regardless of any truth value of the latter in her references (is as it where a consequens in termines).
She is bounded to specific language symbols and structures following conventional rules of syntax and lexicon of a (human) language system.
Both are therefore not directly physically-bound (i.e. not to time, space, energy, matter).
(3) A prejudice is an internal, mental or psychological content, in particular of cognitive nature.
Thus she is bounded to a person or group (performative, author, source). Because of this, she is at least in part, and at least first - through neuro-physiology - physically-bound. Thus she is essentially incidental of nature (although possibly of relative long duration). She precedes in time actual conclusions, decisions, utterances, behavior, etc..
Some mutual relations.
(·) Any given language expression may imply a linguistic presupposition.
(·) A linguistic presupposition may originate from the presence of a psychological (cognitive) content - or, not too rarely, absence of such.
(·) A psychological (cognitive) content may entirely or partly be construed on basis of the presence of prejudice.
(·) A prejudice may come from an invalid inference.
(·) An invalid inference necessarily and simultaneously implies a logical presupposition: i.e. contradiction or definite-contingency.
Notice how only the latter relation is necessarily always valid, and may also be derivable
in a explicit, complete, precise and secure way .. (although dependent of finitely-provability and
decidability).(·) A linguistic presupposition may originate from the presence of a psychological (cognitive) content - or, not too rarely, absence of such.
(·) A psychological (cognitive) content may entirely or partly be construed on basis of the presence of prejudice.
(·) A prejudice may come from an invalid inference.
(·) An invalid inference necessarily and simultaneously implies a logical presupposition: i.e. contradiction or definite-contingency.
Definite-contingency, in formal terms.
A formula F[j] is definitely-contingent:
• F[j] is satisfyable, but invalid;
• F[j] is neither true, nor false;
• The truth-value pattern c[t] of F[j] lies between
• F[j] is neither true, nor false;
• The truth-value pattern c[t] of F[j] lies between
$
0[00..] and$
1[11..];
(·) There exists a formula X[i]) that is logically equivalent to F[j]
, and that is syntactically identical to the maximal semantical reduct of F[j], i.e. F
[j]·
(·) There exists an interpretation i.e. model
equiv-rdc
;
Thus: Assuming X[i] satisfies F[j]) ;
In other words: F[j] presupposes X[i]) .
In other words: F[j] presupposes X[i]) .
M
![m] that is or contains X[i], and (therefore) under which F[j] is valid. {
{  j ( D-CONTIN(F[j] );
j ( D-CONTIN(F[j] );
•  {SATBL(F[j] )
{SATBL(F[j] )  ¬TAUT(
F[j] ) };
¬TAUT(
F[j] ) };
• ( ((¬
( ((¬ F[j])
F[j])
 (¬
(¬ ¬F[j]));
¬F[j]));
• (
(  t ( (F[j]$ =
c[t])
t ( (F[j]$ =
c[t])  (
(
 {SATBL(F[j] )
{SATBL(F[j] )  ¬TAUT(
F[j] ) };
¬TAUT(
F[j] ) };•
 ( ((¬
( ((¬ F[j])
F[j])
 (¬
(¬ ¬F[j]));
¬F[j]));•
 (
(  t ( (F[j]$ =
c[t])
t ( (F[j]$ =
c[t])  (
($
0<
c [t]<
$
1) )t;
(·)  (
(  i ( ( (F[j]
i ( ( (F[j]
 X[i])
X[i])
 (F[j]·
(F[j]·
 ((¬
((¬ X[i])
X[i])
 (¬
(¬ ¬X[i])) );
¬X[i])) );
 (X[i]
(X[i]  F
[j]);
F
[j]);
 (X[i]
(X[i]  (
(
 F[j]));
F[j]));
(·)  (
( m (
m (  X[i] )
X[i] )  (
(
 F[j] ) )m ) )
i ) )j }.
F[j] ) )m ) )
i ) )j }.
 (
(  i ( ( (F[j]
i ( ( (F[j]
 X[i])
X[i]) (F[j]·
(F[j]·equiv-rdc
=
(syn
) X[i]) ((¬
((¬ X[i])
X[i])
 (¬
(¬ ¬X[i])) );
¬X[i])) ); (X[i]
(X[i]  F
[j]);
F
[j]); (X[i]
(X[i]  (
(
 F[j]));
F[j])); (
( m (
m ( M
![m] X[i] )
X[i] )  (
(
M
![m] F[j] ) )m ) )
i ) )j }.
F[j] ) )m ) )
i ) )j }.2.7. Basic Valid and Invalid derivations.
(a)
(Semantical equivalent-reduction; Paraphrase).
(Semantical degressive-reduction; Subsumption).
(Contradiction; Reductio ad absurdum).
Equivalent-validity.
(Semantical equivalent-reduction; Paraphrase).
E.g.: {  h
h  j ( (¬F[h]
j ( (¬F[h]
 G[j])
G[j])  (F[h]
(F[h]
 G[j]) )j ,h }.
G[j]) )j ,h }.
(b)  h
h  j ( (¬F[h]
j ( (¬F[h]
 G[j])
G[j])  (F[h]
(F[h]
 G[j]) )j ,h }.
G[j]) )j ,h }.Degressive-validity.
(Semantical degressive-reduction; Subsumption).
E.g.: {  h
h  j ( (F[h]
j ( (F[h]
 G[j])
G[j])  (
( k
k  l ( (F
[h]
l ( (F
[h]  C[k])
C[k])  (G
[j]
(G
[j]  D[l]) )l ,k ) )
j ,h }.
D[l]) )l ,k ) )
j ,h }.
(c)  h
h  j ( (F[h]
j ( (F[h]
 G[j])
G[j])  (
(degres
) ( k
k  l ( (F
[h]
l ( (F
[h]  C[k])
C[k])  (G
[j]
(G
[j]  D[l]) )l ,k ) )
j ,h }.
D[l]) )l ,k ) )
j ,h }.Contingent-invalidity.
E.g.: {  h
h  j ( (F[h]
j ( (F[h]
 G[j])
G[j])  (
( k ( (F[h]
k ( (F[h]
 D[k])
D[k])  G[j]
)k )
G[j]
)k )  (
(  l ( F[h
]
l ( F[h
]  (G[j]
(G[j]  C
[l]) )l ) ) )j ,h }.
C
[l]) )l ) ) )j ,h }.
(d)  h
h  j ( (F[h]
j ( (F[h]
 G[j])
G[j])  (
(nonseq
) ( ( k ( (F[h]
k ( (F[h]
 D[k])
D[k])  G[j]
)k )
G[j]
)k )  (
(  l ( F[h
]
l ( F[h
]  (G[j]
(G[j]  C
[l]) )l ) ) )j ,h }.
C
[l]) )l ) ) )j ,h }.Inconsistent-invalidity.
(Contradiction; Reductio ad absurdum).
E.g.: {  h
h  j ( (F[h]
j ( (F[h]
 G[j])
G[j])  (
( ¬G[j]) )
j ,h }.
¬G[j]) )
j ,h }.
 h
h  j ( (F[h]
j ( (F[h]
 G[j])
G[j])  (
(contrad
) (F[h] ¬G[j]) )
j ,h }.
¬G[j]) )
j ,h }.
2.8. Validity, Satisfiability and Contingency.
Table 5.
Diagram Validity / Satisfiability / Contingentie |
||
|---|---|---|
1 |
± |
0 |
Not necessarily untrue:Satisfiable,'Logically possible'. (Is not yet equivalent to 'possibly true').
SATBL(G);
 (TAUT(G) (TAUT(G)  D-CONTIN(G); D-CONTIN(G); ¬ ¬ ¬G; ¬G; (( (( G ) G )
 (¬ (¬ ( ( ¬
G ) ) ); ¬
G ) ) ); { {  k ( (G$
= c[k]) k ( (G$
= c[k])  (c[k] (c[k] >$0) )k }; { {  j F[j] j F[j]
 G }; G }; { {  m m M! [m] G }. G }. { {  j ((F[j] j ((F[j]
 ¬F[j]) ¬F[j])  G
) }; G
) }; |
Impossibly true:Unsatisfiable,Logically excluded. 'Excluded grounds'.
¬SATBL(G);
  ¬G; ¬G; { {  k ( (G$
= c[k]) k ( (G$
= c[k])  (c[k] = (c[k] = $0) )k }; {¬ {¬ j ((¬ j ((¬
 ¬F[j]) ¬F[j])  (F
[j] (F
[j]  G)) }; G)) }; {¬ {¬ m m M! [m] G }. G }. { {  j ((F[j] j ((F[j]
 ¬F[j]) ¬F[j])  G
) }; G
) }; |
|
Consistency,Widerspruchsfreiheit. Set K* is consistent: From K* no contradiction is derivable.
CONSIS(K*);
 { ¬( (K* { ¬( (K*  G) G)
 (K* (K*  ¬G) ) }; ¬G) ) }; { ¬(K* { ¬(K* 
 ) }; ) }; { {  j ( ¬( (K* j ( ¬( (K*
 F[j]) F[j])  (K* (K*
 ¬F[j]) )j }; ¬F[j]) )j }; { {  j ( ¬( {K* j ( ¬( {K*
 F[j]} F[j]} 
 ) ) ¬( {K* ¬( {K*  ¬F
[j]} ¬F
[j]}   ) )j
}; ) )j
}; { ¬ { ¬ j ( ( F
[j] j ( ( F
[j]  K* ) K* ) ( ¬F[j] ( ¬F[j]
 K* ) )j }. K* ) )j }. |
Inconsistency,Inconsistent-invalidity. Set K* is inconsistent. From K* a contradiction can be derived.
INCNS(K*);
 ¬CONSIS(K*); ¬CONSIS(K*); { (K* { (K*  G) G)
 (K* (K*  ¬G) }; ¬G) }; { K* { K* 
 }; }; { {  j ( (K* j ( (K*
 F[j]) F[j])  (K* (K*
 ¬F[j])j }; ¬F[j])j }; { {  j ( ( {K* j ( ( {K*
 F[j]} F[j]} 
 ) ) ( {K* ( {K*  ¬F
[j]} ¬F
[j]}   ) )j }; ) )j };
 { {  j ( ( F[
j] j ( ( F[
j]  K* ) K* ) ( ¬F[j] ( ¬F[j]
 K* ) )j }. K* ) )j }. |
|
Consistency theorem,Fundamental theorem (Model-existence theorem): 'Consistency implies Satisfiability'.  (Every subset : (Consistent (Every subset : (Consistent  Satisfiable)).
Satisfiable)).
{CONSIS(K*)
 SATBL(K*)}; SATBL(K*)}; {¬(K* {¬(K* 
 ) )  ¬(K* ¬(K*
  )}. )}. |
||
Necessarily / always true:Valid,Tautology, Valid-satisfiability.
TAUT(G);
  G; G; { {  k ( (G$
= c[k]) k ( (G$
= c[k])  (c[k] = (c[k] = $1) )k }; {¬ {¬ j ((¬ j ((¬
 ¬F[j]) ¬F[j])  (F
[j] (F
[j]  ¬G)) }; ¬G)) }; {¬ {¬ m m M! [m] ¬G }. ¬G }. {¬ {¬ j (F[j] j (F[j]
 ¬F[j] ¬F[j]  G
) }; G
) }; |
Neither true nor false:Definite-Contingency,Contingent-invalidity (invalid but consistent), Contingent-satisfiability (invalid but satisfyable), Insufficiently grounded.
D-CONTIN(G);
 {SATBL(G) {SATBL(G)  ¬TAUT(G)}; ¬TAUT(G)}; {(¬ {(¬ G) G)
 (¬ (¬ ¬G)}; ¬G)}; { {  k ( (G$
= c[k]) k ( (G$
= c[k]) ($0 ($0 <c[k]<$1) )k }; { {  j ((¬ j ((¬
 ¬F[j]) ¬F[j])  (F
[j] (F
[j]  G)) } G)) }  { {  k ((¬ k ((¬
 ¬F[k]) ¬F[k])  (F
[k] (F
[k]  ¬G)) }; ¬G)) }; { ( { ( m m M! [m] G) G) ( ( n n M![n] ¬G) }. ¬G) }. |
|
Not necessarily-true:Invalid,non sequitur [nonseq]:
NONSEQ(G);
 ¬TAUT(G); ¬TAUT(G); (D-CONTIN(G) (D-CONTIN(G)  ¬SATBL(G); ¬SATBL(G); ¬ ¬ G; G; { {  k ( (G$
= c[k]) k ( (G$
= c[k])  (c[k] (c[k] <$1) )k }; { {  j ((¬ j ((¬
 ¬F[j]) ¬F[j])  (F
[j] (F
[j]  ¬G)) }; ¬G)) }; { {  m m M! [m] ¬G }. ¬G }. |
||
Correctness(Soundness in-formele-zin): 'Derivable implies logical consequence'. Set K* is correct.  (Every subset : (Every subset :(Derivable  Logical consequence). Logical consequence).
CORRECT(K*);
 {DRVBL(K*,G) {DRVBL(K*,G)  SEQUIT(K
*,G)}; SEQUIT(K
*,G)}; { (K* { (K*  G) G)
 (K* (K*  G) }; G) }; { {  j ( (K* j ( (K*
 F[j]) F[j])  (K* (K*
 F[j]) ) }. F[j]) ) }. |
||
Completeness(Vollständigkeit). 'Validity implies Derivability'. Set K* is complete:  (Every subset : (Every subset :(Logical consequence  Derivable)). Derivable)).
COMPLET(K*);
 {SEQUIT(K*,G) {SEQUIT(K*,G)  DRVBL(K
*,G)}; DRVBL(K
*,G)}; { (K* { (K*  G) G)
 (K* (K*  G) }; G) }; { {  j ( (K* j ( (K*
 F[i]) F[i])  (K* (K*
 F[j]) ) }. F[j]) ) }. |
||
Maximal consistency:Set K* is maximally consistent:  (Every subset : (Every subset :(Logical consequence  Derivable)). Derivable)).
MAXCONS(K*);
 { CONSIS(K*) { CONSIS(K*)  COMPLET(K*
) }; COMPLET(K*
) }; { (K* { (K*  G) G)
 (K* (K*  G) }; G) }; { {  j ( (K* j ( (K*
 F[j]) F[j])  (K* (K*
 F[j]) )j }; F[j]) )j }; { {  j ( CONSIS(K* \ {F
[j]}) j ( CONSIS(K* \ {F
[j]}) ¬CONSIS(K* ¬CONSIS(K*  {F
[j]}) )j }; {F
[j]}) )j }; { {  j ( ( (F[j] j ( ( (F[j]
 K*) K*) ( {K* ( {K*  ¬F
[j]} ¬F
[j]}   ) ) ) ) ( ¬(F[j] ( ¬(F[j]  K
*) K
*) ¬( {K* ¬( {K*
 F[j]} F[j]} 
 ) ) )j }; ) ) )j };Implications:  { {  j ( (F[j] j ( (F[j]
 K*) K*)||(¬F[j] K
*) )j }; K
*) )j }; |
|
|
|
(·) Completeness of PPL: proof by Emil L. Post (1920, Introduction to a general theory of elementary propositions). (·) Completeness of PDL-I: proof by Kurt F. Gödel (1929/1930, Über die Vollständigkeit des Logikkalküls). |
(·) Incompleteness of elementary arithmetic (first-order theory of natural numbers according to
the logicistic research program, that was based on classic logic in the Organon of
Aristotelis, and had been further developed in the Grundgesetze der Arithmetik of F.L. Gottlob Frege
(1893, 1903) and the Principia Mathematica of Bertrand Russell and Alfred North Whitehead,
parts I-III (1910, 1912, 1913): proved by Kurt Gödel (1931, Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme 1). |
|
2.9. Relations between logical criteria of level II.
(1)
(By assumption or (re)presentation).
'From strong to weak'.
 ( Valid
( Valid  Satisfiable /
Consistent ).
Satisfiable /
Consistent ).
 ( Definitely-Contingent
( Definitely-Contingent  Satisfiable /Consistent ).
Satisfiable /Consistent ).
 ( Definitely-Contingent
( Definitely-Contingent  Invalid
).
Invalid
).
 ( Unsatisfiable /Inconsistent /Contradiction
( Unsatisfiable /Inconsistent /Contradiction
 Invalid ).
Invalid ).
 ( Onvervulbaar /Inconsistent /Contradictie
( Onvervulbaar /Inconsistent /Contradictie
 ( Valid
( Valid
Valid statement or inference.
(By assumption or (re)presentation).
'From strong to weak'.
 ( Valid
( Valid  Satisfiable /
Consistent ).
Satisfiable /
Consistent ). ( Definitely-Contingent
( Definitely-Contingent  Satisfiable /Consistent ).
Satisfiable /Consistent ). ( Definitely-Contingent
( Definitely-Contingent  Invalid
).
Invalid
). ( Unsatisfiable /Inconsistent /Contradiction
( Unsatisfiable /Inconsistent /Contradiction
 Invalid ).
Invalid ). ( Onvervulbaar /Inconsistent /Contradictie
( Onvervulbaar /Inconsistent /Contradictie #
Satisfiable /Consistent ). ( Valid
( Valid #
Invalid ).Level III.
Decidability and Recursivity of formal systems
Table 6.
Diagram Decidability and Recursivity |
|||
|---|---|---|---|
1 |
± |
||
Decidable:The question whether an expression G has a definite (truth) value, can always be answered:  The (truth) value of G is always derivable through a finite proof. The (truth) value of G is always derivable through a finite proof. |
UnDecidable:The question whether an expression G has a definite (truth) value, can not always be answered:  The (truth) value of G is not always derivable through a finite proof. The (truth) value of G is not always derivable through a finite proof.
|
||
|
G is Truth-value Decidable:
DECIDBL(G);
 {( {(  ( G ( G
 $1) )||( ( G ( G  $0) ) }; {( {(  ( (
 G ) ) G ) ) ||( ( (  ¬G ) ) }; ¬G ) ) };Implications:  { {  ( ( ( (
 G ) G ) ||( ¬G ) ) }. ¬G ) ) }. { {  ( (
 ( G ( G ||¬G ) ) }; { {  ( G ( G
||¬G ) }; { G { G ||¬G } (always logical value). $1 (truth). |
G is Not truth-value deDecidable:
¬DECIDBL(G);
 { (¬ { (¬ ( G ( G
 $1) ) (¬ (¬
 ( G ( G  $0) ) }; { (¬ { (¬ ( (
 G ) ) G ) )  (¬ (¬
 ( (  ¬G ) ) }; ¬G ) ) };Implications:  { ¬ { ¬ ( ( ( (
 G ) G ) ||( ¬G ) ) }; ¬G ) ) }; { ¬ { ¬ ( (
 ( G ( G ||¬G ) ) }; { ¬ { ¬ ( G ( G
||¬G ) }; { } (no logical value); { } (no logical value); $0 (no truth). |
||
G is Validity Decidable: { ( { ( ( (
 G) ) G) ) ||( (¬ (¬ G) ) }; G) ) };Implications:  { {  ( ( ( (
 G ) G ) ||( ¬ G ) ) }; G ) ) }; { ( { (  G ) G )
||( ¬ G ) }. G ) }. { TAUT(G) { TAUT(G) ||¬SATBL(G ) } (always validity value). $1 (truth).G is determinate. |
G is Not validity Decidable: { (¬ { (¬ ( (
 G) ) G) )  (¬ (¬
 (¬ (¬ G) ) }; G) ) };Implications:  { ¬ { ¬ ( ( ( (
 G ) G ) ||( ¬ G ) ) }. G ) ) }. { ¬( { ¬(  G ) G )
 ¬( ¬(  ¬G ) }. ¬G ) }. { D-CONTIN(G) } (no validity value). { D-CONTIN(G) } (no validity value). $0 (no truth).G is indeterminate. |
||
Recursive:For all input, the system will be 'halting' (terminating in finite time). |
Non-recursive:For some input the system will be infinitely 'looping'. |
||
|
RC(G);
 { RE(G) { RE(G)  CO-RE(G
) }; CO-RE(G
) }; { ( { ( ( (
 G) ) G) ) ||( (¬ (¬ G) ) }; G) ) };Implications:  { {  ( ( ( (
 G) G) ||(¬ G) ) }. G) ) }. |
¬RC(G);
 { ¬RE(G) { ¬RE(G)  ¬CO-RE(G
) }. ¬CO-RE(G
) }. { (¬ { (¬ ( (
 G) ) G) )  (¬ (¬
 (¬ (¬ G) ) }; G) ) };Implications:  { ¬ { ¬ ( ( ( (
 G) G) ||(¬ G) ) }. G) ) }. |
||
Recursively |
Co-recursively |
|
|
|
Set K* is Recursively enumerable: If K* has a result, then that will always be provable.
RE(K*);
 { {  k ( (Ks*[k] k ( (Ks*[k]
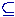 K*) K*)  j ( (Ks*[k] j ( (Ks*[k]
 F[j]) F[j])  (Ks*[k] (Ks*[k]
 F[j]) )j )k }. F[j]) )j )k }. |
Complement of K* is Recursively enumerable: If K* has no result, then that will always be provable.
CO-RE(K*);
 { {  k ( (Ks*[k] k ( (Ks*[k]
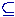 K*) K*)  j ( ¬(Ks*[k] j ( ¬(Ks*[k]
 F[j]) F[j])  ¬(Ks*[k] ¬(Ks*[k]
 F[j]) )j )k }. F[j]) )j )k }. |
Set K* is not Recursively enumerable: If K* has a result, then that will not always be provable.
¬RE(K*);
 { {  k ( (Ks*[k] k ( (Ks*[k]
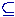 K*) K*)  j ( (Ks*[k] j ( (Ks*[k]
 F[j]) F[j]) ¬ ¬ (Ks*[k] (Ks*[k]
 F[j]) )j )k }. F[j]) )j )k }. |
Complement of K* is not Recursively enumerable: If K* has no result, then that will not always be provable.
¬CO-RE(K*);
 { {  k ( (Ks*[k] k ( (Ks*[k]
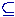 K*) K*)  j ( ¬(Ks*[k] j ( ¬(Ks*[k]
 F[j]) F[j]) ¬ ¬ ¬(Ks*[k] ¬(Ks*[k]
 F[j]) )j )k }. F[j]) )j )k }. |
|
Set K* is Recursively enumerable (through Turing Machine procedure): If K* has a result, then that will always be computable.
RE(K*)TM;
 { {  k ( (Ks*[k] k ( (Ks*[k]
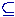 K*) K*)  j j
 h ( h ((TM[h](Ks*[k])  F
[j]) F
[j])  m (TM[m]
(K*) m (TM[m]
(K*)  (TM[h](Ks*[k])  F[j]) )m )h ,j )
k }. F[j]) )m )h ,j )
k }. |
Complement of K* is Recursively enumerable (through Turing Machine procedure): If K* has no result, then that will always be computable.
CO-RE(K*)TM;
 { {  k ( (Ks*[k] k ( (Ks*[k]
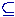 K*) K*)  j j
 h ( h (¬(TM[h](Ks*[k])  F
[j]) F
[j])  m ( (TM[m]
(K*) m ( (TM[m]
(K*)  ¬(TM[h](Ks*[k])  F[j]) )m )h ,j )
k }. F[j]) )m )h ,j )
k }. |
Set K* is not Recursively enumerable (through Turing Machine procedure): If K* has a result, then that will not always be computable.
¬RE(K*)TM;
 { {  k ( (Ks*[k] k ( (Ks*[k]
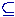 K*) K*)  j j
 h ( h ((TM[h](Ks*[k])  F
[j]) F
[j]) ¬ ¬ m (TM[m](
K*) m (TM[m](
K*)  (TM[h](Ks*[k])  F[j]) )m )h ,j )
k }. F[j]) )m )h ,j )
k }. |
Complement of K* is not Recursively enumerable (through Turing Machine procedure): If K* has no result, then that will not always be computable.
¬CO-RE(K*)TM;
 { {  k ( (Ks*[k] k ( (Ks*[k]
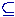 K*) K*)  j j
 h ( h (¬(TM[h](Ks*[k])  F
[j]) F
[j]) ¬ ¬ m (TM[m](
K*) m (TM[m](
K*)  ¬(TM[h](Ks*[k])  F[j]) )m )h ,j )
k }. F[j]) )m )h ,j )
k }. |
|
(·) 'Effective procedure' (Hilbert, 1900, 1928). (·) 'Recursive function' (Gödel, 1930, 1931). (·) 'Lambda definable function' (Church, 1935, 1936). (·) 'Turing Machine computable function' (Turing, 1936, 1937). |
(·) UnDecidability/ non-recursivity of elementary calculus of natural numbers (elementary number theory): proof by Alonzo Church, (1935/1936, An Unsolvable Problem of Elementary Number Theory). (·) UnDecidability/ non-recursivity of entire elementary arithmetic (first order arithmetic): proof by Alan M. Turing (1936/1937, On computable numbers, with an application to the Entscheidungsproblem ). |
||
4.
Table with Some Milestones in Meta-logic
Table 7.
| Author | Year | Formalism | Domain | Criterion | |
|---|---|---|---|---|---|
| Hilbert | 1900,1928 | Effective procedure (hypothetical) | Mathematics, Logic |
Decidability; Entscheidbarheit; Entscheidungs-definitheit; |
|
| Post | 1920 |
Truth table method |
PPL |
Completeness; Vollständigkeit. |
|
| Gödel | 1929/1930 | Deduction | PDL-I |
Completeness; Vollständigkeit. Recursively enumerable |
|
| Gödel | 1931 | Gödel-numbering |
PDL-I, Arithmetic of Natural numbers First-order theory of natural numbers (Principia Mathematica) |
Einige formal unentscheidbare Satze: Incompleteness; Unvollständigkeit. Not recursively enumerable. |
|
| Church | 1935/1936 |
Lambda-calculus (Lambda-definable): Recursive functions of positive integers |
PDL-I, Arithmetic of Natural numbers: Elementary number theory |
Unsolvable problem: UnDecidability; Unentscheidbarheit. |
|
| Turing | 1936/1937 |
(Universal) Turing machine (Turing machine computability) |
PDL-I, Arithmetic: First order arithmetic |
UnDecidability; Unentscheidbarheit. |
Criteria in formal logic
In the overview ' Criteria in Formal Logic' the most important criteria in formal logic are being discussed.
These criteria may be applied to formulas, sentences, sets, theories and (language) systems in logic.
They are meant to represent entirely accurate the most essential characteristics of certain data: quality, scope, possibilities but also limitations.
Criteria in Formal Logic
(1)
Criteria for decisions about content aspects of language expressions.
A.o. satisfiability, validity, (definitely-)contingency, finite-satisfiability, compactness, etc..
(2)
Criteria for decisions about aspects of form and structure of statements.
Correctness: A.o. derivability, provability, consistency.
(3)
Ie. projections from semantics to syntax.
A.o. completeness.
(4)
Ie. projections from syntax to semantics.
A.o. consistency theorem, correctness, Decidability.
Semantic criteria
Criteria for decisions about content aspects of language expressions.
A.o. satisfiability, validity, (definitely-)contingency, finite-satisfiability, compactness, etc..
(1a) Satisfiability: (Logical possibility): Truth under at least one possible interpretation.
 ((Well-formed
((Well-formed  not-Refuted)
not-Refuted)
 Satisfiable).
Satisfiable).
(1b) Validity (tautology):) Truth under any possible interpretation.
 ((Well-formed
((Well-formed  always-True)
always-True)
 Valid).
Valid).
(1c) Definitely-contingency: Satisfiable, but not valid.
(Truth under at least one possible interpretation, maar not all).
 ((Well-formed
((Well-formed  (Satisfiable
(Satisfiable
 not-Valid))
not-Valid))  Definitely-contingent
).
Definitely-contingent
).
(1d) Finite-satisfiability: A (sub)set of formulas is finite and satisfiable.
 (((Sub)set
(((Sub)set  (Well-formed
(Well-formed
 (Finite
(Finite  Satisfiable)))
Satisfiable)))
 Finite-satisfiable).
Finite-satisfiable).
(1e) Compactness: If every finite subset of a - possibly infinite - set is satisfiable,
that the entire set is satisfiable.
 (((Every subset: (Well-formed
(((Every subset: (Well-formed  Finitely satisfiable))
Finitely satisfiable))  Satisfiable)
Satisfiable)
 Compact).
Compact).
 ((Well-formed
((Well-formed  not-Refuted)
not-Refuted)
 Satisfiable).
Satisfiable). ((Well-formed
((Well-formed  always-True)
always-True)
 Valid).
Valid).(Truth under at least one possible interpretation, maar not all).
 ((Well-formed
((Well-formed  (Satisfiable
(Satisfiable
 not-Valid))
not-Valid))  Definitely-contingent
).
Definitely-contingent
). (((Sub)set
(((Sub)set  (Well-formed
(Well-formed
 (Finite
(Finite  Satisfiable)))
Satisfiable)))
 Finite-satisfiable).
Finite-satisfiable). (((Every subset: (Well-formed
(((Every subset: (Well-formed  Finitely satisfiable))
Finitely satisfiable))  Satisfiable)
Satisfiable)
 Compact).
Compact).(2)
Syntactical criteria.
Criteria for decisions about aspects of form and structure of statements.
Correctness: A.o. derivability, provability, consistency.
(2a) Derivability: Derivable through syntactical production rules.
 ((Well-formed
((Well-formed  result of accurate formal operations)
result of accurate formal operations)  Derivable).
Derivable).
(2b) Provability (finite-derivability): Syntactical derivable through a finite
derivation chain.
 (((Well-formed
(((Well-formed  result of finite
series of purely formal operations)
result of finite
series of purely formal operations)  Finite-derivable)
Finite-derivable)
 Provable).
Provable).
(2c) Consistency: Derivable guarantees non-contradiction.
 (For any subset: ((Derivable
(For any subset: ((Derivable  Non-contradiction)
Non-contradiction)  Consistent)).
Consistent)).
(2d) Maximal consistency: Consistency guarantees inconsistency with every possible semantic/i>
(ie. nonredundant, conjunctive) expansion.
 ((Consistent
((Consistent  (adding of any other formula
(adding of any other formula
 inconsistent))
inconsistent))  Maximally consistent
).
Maximally consistent
).
(2e) Negation-completeness: A set K* contains for every well-formed formula in the language
either the confirmation, or the negation.
 ((Every subset: (Well-formed
((Every subset: (Well-formed  (Truth decision
(Truth decision  (either True, or False))))
(either True, or False))))
 Negation-complete).
Negation-complete).
 ((Well-formed
((Well-formed  result of accurate formal operations)
result of accurate formal operations)  Derivable).
Derivable). (((Well-formed
(((Well-formed  result of finite
series of purely formal operations)
result of finite
series of purely formal operations)  Finite-derivable)
Finite-derivable)
 Provable).
Provable). (For any subset: ((Derivable
(For any subset: ((Derivable  Non-contradiction)
Non-contradiction)  Consistent)).
Consistent)). ((Consistent
((Consistent  (adding of any other formula
(adding of any other formula
 inconsistent))
inconsistent))  Maximally consistent
).
Maximally consistent
). ((Every subset: (Well-formed
((Every subset: (Well-formed  (Truth decision
(Truth decision  (either True, or False))))
(either True, or False))))
 Negation-complete).
Negation-complete).(3)
Semantical criteria, in relation to syntax:
Ie. projections from semantics to syntax.
A.o. completeness.
(3a) Syntactical - Adequacy.
Satisfiability guarantees Consistency.
 ((Every subset: (Satisfiable
((Every subset: (Satisfiable  Consistent))
Consistent))  Adequate).
Adequate).
(3b) Syntactical - Completeness (proof potential, Vollständigkeit): Truth/ validity
guarantees Derivability.
 ((Every subset: (True/ valid
((Every subset: (True/ valid  Derivable))
Derivable))  Complete).
Complete).
Satisfiability guarantees Consistency.
 ((Every subset: (Satisfiable
((Every subset: (Satisfiable  Consistent))
Consistent))  Adequate).
Adequate). ((Every subset: (True/ valid
((Every subset: (True/ valid  Derivable))
Derivable))  Complete).
Complete).(4)
Syntactical criteria, in relation to semantics:
Ie. projections from syntax to semantics.
A.o. consistency theorem, correctness, Decidability.
(4a) Fundamental theorem, consistency theorem: Consistency guarantees satisfiability.
 ((Every subset: (Consistent
((Every subset: (Consistent  Satisfiable))
Satisfiable))  Fundamental theorem).
(4b) Logical correctness of formal systems ('soundness', in weak sense, deductive power):
Derivability guarantees Validity.
Fundamental theorem).
(4b) Logical correctness of formal systems ('soundness', in weak sense, deductive power):
Derivability guarantees Validity.
 ((Every subset: (Derivable
((Every subset: (Derivable  True/ Valide))
True/ Valide))  Correct)).
Correct)).
(4c) Logical 'soundness' of formal systems (in strong sense): Derivability guarantees
Logical Consequence.
 ((Every subset: (Derivable
((Every subset: (Derivable  Logical consequent))
Logical consequent))  Sound).
Sound).
(4d) Reductio ad absurdum: Logical validity guarantees Non-contradiction.
 ((Well-formedness
((Well-formedness  (Opposite/Negation
(Opposite/Negation
 (Some conjunct subset: (Contradiction derivable: inconsistent))))
(Some conjunct subset: (Contradiction derivable: inconsistent))))
 True/ Valid).
True/ Valid).
(4e) Decidability (decision capacity) of formal systems: Syntactical well-formedness
guarantees validity decision.
 (Well-formedness
(Well-formedness  (Validity decision:
(Validity decision:
 (either Valid, or Invalid)))
(either Valid, or Invalid)))  Validity
Decidable).
Validity
Decidable).
 ((Every subset: (Consistent
((Every subset: (Consistent  Satisfiable))
Satisfiable))  Fundamental theorem).
Fundamental theorem).
 ((Every subset: (Derivable
((Every subset: (Derivable  True/ Valide))
True/ Valide))  Correct)).
Correct)). ((Every subset: (Derivable
((Every subset: (Derivable  Logical consequent))
Logical consequent))  Sound).
Sound).
In other words, from provability of contradiction derived from the opposite, follows logical validity.
Principle of proof by 'refutation of the opposite'.
Principle of proof by 'refutation of the opposite'.
 ((Well-formedness
((Well-formedness  (Opposite/Negation
(Opposite/Negation
 (Some conjunct subset: (Contradiction derivable: inconsistent))))
(Some conjunct subset: (Contradiction derivable: inconsistent))))
 True/ Valid).
True/ Valid). (Well-formedness
(Well-formedness  (Validity decision:
(Validity decision:
 (either Valid, or Invalid)))
(either Valid, or Invalid)))  Validity
Decidable).
Validity
Decidable).C.P. van der Velde © 2006, 2018.