Cursus / training:
Methode voor Logische Analyse
Principes van Formele logica.
Combinatorische explosie in Logische systemen
Inhoudsopgave
Combinatorische explosie in Logische systemen
Inleiding: Informatie, logica en complexiteit.
Oordeelsvorming maakt gebruik van informatie
Onze oordelen en inschattingen lijken in veel opzichten op onze overige reacties en beslissingen. We baseren ze op informatie die we beschikbaar hebben, op bewust maar ook op onbewust niveau.
Informatie en verschil.
Over het begrip 'informatie' zijn veel verschillende opvattingen. Om misverstanden te vermijden, en de wezenlijke betekenis van het begrip te begrijpen, is het handig om eerst te kijken naar haar meest kenmerkende eigenschap. Die wordt duidelijk wanneer we ons de situatie voorstellen waarin ze er totaal níet is. Zonder enige informatie is er alleen zinloze chaos, nietszeggende ruis (noise), totale vaagheid, een volstrekt niet-weten.
Informatie begint pas bij onderscheiding van enig verschil. Zodra een onderscheid valt te maken - bijv. een verschil tussen wel/niet, aan/uit, ja/nee, waar/onwaar, enz. - ontstaat enige ordening. Alleen dan wordt redeneren mogelijk, en is de logica van toepassing. Elke hoeveelheid informatie impliceert dus minstens één verschil.
Informatie en ordening.
Elk verschil impliceert op zijn beurt minstens twee 'dingen', verschijnselen of toestanden in een gebied in de werkelijkheid. Op basis van onderscheidingen kunnen dus combinaties van dingen worden beschouwd.
Tussen die dingen bestaat tegelijk minstens één ordeningsrelatie, namelijk die welke noodzakelijk volgt uit datzelfde bespeurde verschil.
Bovendien, om enige betekenis voor ons te hebben, kan informatie sowieso niet bestaan uit louter losse gegevens. We bekijken informatie altijd in een bepaalde samenhang. Dit impliceert dat ze de mogelijkheid biedt ordening te onderscheiden.
Omgekeerd bezien vertegenwoordigt elke ordeningstoestand, of structuur, op zichzelf genomen een bepaald gehalte aan informatie.
Logische relaties.
Gegeven een willekeurige verzameling elementen kunnen we kijken welke logische relaties tussen die elementen mogelijk zijn.
De logische relaties hebben betrekking op de verschillende toestanden of waarden die de elementen afzonderlijk kunnen aannemen, alsook door hun onderlinge afleidingsrelaties.
Informatie en redenering.
Door het combineren van gegevens kunnen we meer complexe vormen van informatie verkrijgen.
Dit doen we uiteraard door middel van onze gedachten.
Elke gedachtegang, en in feite elk proces van informatieverwerking, heeft de algemene vorm van een redenering, dat wil zeggen:
Redeneren:
Een aantal uitgangsgegevens worden gecombineerd, en uit de combinatie worden volgende gegevens afgeleid.
De manieren waarop die combinaties kunnen worden gemaakt, en de waarden die deze combinaties kunnen aannemen, worden bepaald door
de wetten van de logica.Een aantal uitgangsgegevens worden gecombineerd, en uit de combinatie worden volgende gegevens afgeleid.
Uiteraard gelden deze eigenschappen ook en bij uitstek voor elke oordeelsvorming. Die kan beschouwd worden als redeneervorm, omdat ze aangrijpt op informatie, en vervolgens resulteert in bepaalde informatie.
Logische wetten.
De logische wetten hebben louter betrekking op de relaties tussen gegevens, dat wil zeggen de combinaties en afleidingen; en niet op de afzonderlijke gegevens (zoals directe waarnemingen en gevoelens). Ze gelden ook onafhankelijk van de inhoud en de aard van de gegevens, m.n. mogelijke variaties in onderwerp, domein, probleem, doel, toepassing, toepassingsgebied, enz..
Trappen van logische complexiteit.
Elke redeneervorm bestaat uit een combinatie van één of meer onderscheiden logische relaties.
Redeneringen zijn - letterlijk - in elke denkbare vorm mogelijk, maar ook in elke ondenkbare vorm: ze zijn vrijwel onbeperkt in mogelijke variatie, complexiteit en omvang. Zoals we hieronder zullen zien, reikt dit al in een klein aantal stappen onafzienbaar ver buiten het voorstellings- en bevattingsvermogen van mensen, en evengoed buiten de reken- en opslagcapaciteit van fysieke of zelfs theoretische computers van elke voorstelbare omvang.
Gelukkig kunnen al die mogelijke vormen worden geordend en beoordeeld met behulp van de wetten van de logica. Inzicht in de wetten van de logica is daarom onontbeerlijk voor elke zinvolle en betrouwbare oordeelsvorming. Voor het optimaal benutten van de logica is een helder inzicht in de minimale niveau's van logische complexiteit en hun proporties onmisbaar.
1.
Grondslagen van een Logisch systeem.
In dit overzicht kijken we naar de logische mogelijkheden die volgen uit een willekeurige verzameling eenheden (items of objecten). We zullen daarbij zien op welke manieren hierbij combinatorische explosie optreedt, in welke mate dit gebeurt en welke consequenties dit heeft voor de complexiteit van informatieverwerking en oordeelsvorming met betrekking tot de uitgangsgegevens.
Om ons te beperken tot de meest algemeen geldige principes gaan we uit van een logische systeem dat zelf van minimale complexiteit is. Uit dit systeem kan de propositielogica worden afgeleid, maar ook, met de nodige aanvullingen, iets complexere systemen zoals de predicatenlogica en de modale logica.
In het algemeen geldt dat de consequenties van combinatorische explosie en complexiteit zelf explosief toenemen met elke trap van toenemende verfijning van het logische systeem dat we toepassen.
Logisch systeem op semantisch niveau.
S!
: een logisch systeem ('apparaat', calculus).S!
PPL :S!
is een systeem in de propositielogica (PPL
) (of hoger).S!
PDL-I :S!
is een systeem in de predicatenlogica (PDL-I
), first-order logic (FOL
) (of hoger).S!
) : de semantiek, een verzameling ordeningsregels, vanS!
.Logisch systeem op syntactisch niveau.
L!
: een formeel systeem (taalsysteem).L!
PPL :L!
is een taal in de propositielogica (PPL
) (of hoger).L!
PDL-I :L!
is een taal in de predicatenlogica (PDL-I
), first-order logic (FOL
) (of hoger).L!
) : de syntax, of grammatica, een verzameling ordeningsregels, vanL!
.WFF*(
L!
) : de verzameling welgevormde uitspraken (well-formed formulas) vanL!
.Basisparameters.
1.1.
Objecten.
Toepasbaar in
PPL
en hoger.D
* : (referentieel) domein of populatie, verzameling elementen d[d1] ; waarbij (d1=
1,..
d).d : domein- of populatie-omvang; totaal aantal unieke objecten, domein-elementen ('dingen', fenomenen , items, variabelen) d[d1] in
D
*.D
*=
{d[1], .. d[d1], .. d[d] }.d
=
|
D
*|
.Voorbeeld.
Bij twee items (d
=
2 ) kan de verzamelingD
·d bestaan uit de volgende elementen (objecten), hier weergegeven met propositiesymbolen en in arbitraire volgorde:
{ (d =
2 )(D
·d=
{' A' ,' B'} ) }.S!
[s1] dan wel uiterst minimaal, zo niet futiel.Enkele voorbeelden van beweringen in zo'n 'minimaal' systeem, in een formele taal:
{ (d =
0 )(D
·d=
{} ) : ({}=
(v) {} ); (({})$
=
(v)$
0 ); ({}=
(r)$
0 ); etc.}.S!
[s1] ook buitengewoon simpel.Enkele voorbeelden van beweringen in zo'n 'primitief' systeem, in een formele taal:
{ (d =
1 )(D
*=
{d[1]} ) : ((d[1] )$
=
(v)$
1 ); ((d[1] )$
=
(v)$
0 ); etc.}.Bereik.
Wanneer het aantal objecten minder dan één is, wordt elke redenering zinloos.
Wanneer het echter oneindig is, worden onnoemelijk veel redeneringen over het domein in de praktijk onbeslisbaar.
Voor een domein dat zinvol is en hanteerbaar (manageable), geldt:
{ (d (1 
0 ) }.
=
|
D
*(mgb
)|
);(1 ≤
d<
0 ) }.1.2.
Waarden.
Algemeen toepasbaar op objecten.
V
* : waarderingsstelsel of 'waardenpalet', verzameling waarden v[v1]; waarbij (v1=
1,..
v).v : totaal aantal unieke waarden, toestandswaarden, objectwaarden of signaalwaarden ( valenties, schaal); bijv. waarheidswaarden, v[v1] in
V
*.V
*=
{v[1], .. v[v1], .. v[v] }.v
=
|
V
*|
.Voorbeeld.
Bij twee waarden (v
=
2 ) kan de verzamelingV
·v bestaan uit de volgende elementen (waarden), hier weergegeven met waarde constanten en in arbitraire volgorde:{ (v =
2 )(V
·v=
{0 ,1 } ) }.Bereik.
Wanneer het aantal waarden minder dan twee is, wordt elke toekenning van waarde betekenisloos, en daardoor wordt elk begin van een zinnige redenering onmogelijk.
Wanneer dit aantal echter oneindig is, wordt vrijwel elke redenering over het domein in de praktijk onbeslisbaar.
Voor een waardenpalet dat zinnig is en hanteerbaar (manageable), geldt:
{ (v (2
0 ) }.
=
|
V
*(mgb
)|
);(2 ≤
v<
0 ) }.1.3.
Parameters voor Predikatenlogica.
In de
PDL
komen daarbij nog aanvullende parameters.
(2a) p : totaal aantal unieke predikaat-variabelen (attributen, predikaatnamen); waaronder evt. identiteit, '='.
(2b) r : (maximaal) totaal aantal unieke argument-plaatsen, of ariteit, per predikaatnaam.
(neem hiervoor omwille van eenvoud en zekerheid eventueel het maximum over alle predikaatnamen).
(2c) n : totaal aantal unieke elementen (individuen, objecten) in het referentieel domein (de populatie).
Het (maximaal) aantal unieke items a is in (2b) r : (maximaal) totaal aantal unieke argument-plaatsen, of ariteit, per predikaatnaam.
(neem hiervoor omwille van eenvoud en zekerheid eventueel het maximum over alle predikaatnamen).
(2c) n : totaal aantal unieke elementen (individuen, objecten) in het referentieel domein (de populatie).
PDL
van deze laatste drie een afgeleide.{p ≤
a≤
(p *MAX(1,(r*
n)) }.PDL
systeem voldoende informatie over de parameters p, r en n , dan kunnen we a berekenen en verder redeneren conform de regels voor eenPPL
systeem.Hieronder onderzoeken we welke combinatorische mogelijkheden deze parameters opleveren op semantisch respectievelijk syntactisch vlak.
2.
Semantische expansie.
2.1.
Elementaire objecttoestanden .
Objecttoestanden worden gevormd door paren, of tupels (het Cartesisch product) uit de v waarden en d elementen.
Ze geven het domein weer op een observationeel niveau.
Op semantisch niveau zijn dit waarheidsbeweringen met betrekking tot de toestand van afzonderlijke objecten.
In logische talen zijn dit bijv. literalen, grondinstanties, of 'witnesses'.
Deze zijn te vergelijken met steekproeven (samples) uit een populatie.
H
·(v,d) : De verzameling van alle mogelijke unieke objecttoestanden .Voorbeeld.
In het simpelste, universeel toepasbare logisch systeem, met twee waarheidswaarden (v
=
2, binair systeem ) en twee items (d=
2), bestaat de verzamelingH
·(v,d ) uit de volgende elementen (objecttoestanden), hier weergegeven met propositiesymbolen en in arbitraire volgorde:(H
·(v=
2,d=
2)=
{ ' A' ,'¬A' ,' B' ,'¬B' } ).Omvang.
h(v,d) : Het totale aantal mogelijke unieke objecttoestanden.
{ 
v d
( h(v,d) :=
|
H
·(v,d)|
;:=
(|
V
·v|
,|
D
·d|
;:=
v*
d )d, v }.In een binair systeem.
Onder (v
=
2 ) geldt:H
·(v,d) is even groot als de verdubbeling van verzamelingD
·d.De waarden h(2,d) komen overeen met de natuurlijke niet-negatieve even getallen. Zie reeks A005843 (eerder M0985) in de On-line Encyclopedia of Integer Sequences (OEIS).
{ d ( h(2,d) :=
2*
d;:=
A005843(d )|
(offset 0 ) )d }.
Bijv., bij (d
volgt (h(2,d)
=
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..
} );volgt (h(2,d)
=
{ 2, 4, 6, 8, 10, 12, 14, 16, 18, 20,..
} ).Bereik.
Het getal h(v,d) blijft lineair (polynomiaal) in d.
(2 ≤
h(v,d)<
0 ).Complexiteitsklasse.
De verzameling
H
·(v,d) blijft binnen de klasse van aftelbaar oneindige verzamelingen (countable infinite sets, denumerable sets).Is dus algoritmisch doorzoekbaar (tracktable) - met een singletape Turing machine - binnen lineair polynomiale rekentijd (
P-TIME
).(H
·(v,d)
POLY
(d^1 );TIME
(d );
P-TIME
).2.2.
Domeintoestanden.
Domein toestanden bestaan uit conjuncte combinaties van alle objecten met hun specifieke waarden, dus verschillende objecttoestanden.
Ze geven het domein weer op een louter beschrijvend niveau.
Op semantisch niveau zijn dit waarheidsbeweringen met betrekking tot de toestand van het gehele domein dat we in ogenschouw nemen.
Ze zijn te vergelijken met de cellen (categorieën van variantie) van een zgn. contingentie tabel (cross tabulation , of 'crosstab'), die de grondslag vormt voor talrijke statistische maten voor de vergelijking van varianties, met name Chi-kwadraat (Χ2), en varianten of afgeleiden daarvan, zoals correlatie coëfficiënt, regressie coëfficiënt, Student's t, F, Fisher z, enz..
B
·(v,d) : De verzameling van alle mogelijke unieke domeintoestanden .Voorbeeld.
Bij twee waarheidswaarden (v
=
2, binair systeem) en twee items (d=
2) bestaat de verzamelingB
·(v,d) uit de volgende elementen (domeintoestanden), hier weergegeven met propositiesymbolen en in arbitraire volgorde:(B
·(v=
2,d=
2)=
{'( A
B)' ,'( A
¬B)' ,'(¬A B)' ,'(¬A ¬
B)' } ).Omvang.
b(v,d) : Het totale aantal mogelijke unieke domeintoestanden.
Het getal b(v,d) komt overeen met het aantal herhalingsvariaties, oftewel, volgordevariaties met teruglegging c.q. herhaling, met omvang (lengte) d uit v elementen.
{ v d
( b(v,d) :=
|
B
·(v,d)|
;:=
(d1 := 1, ..
d ) v;:=
v ^d;:=
b(v,d -1 )*
v )d, v }.Het is gelijk aan het aantal rijen in de waarheidswaardetabel.
In een binair systeem.
Onder (v
=
2 ) geldt:B
·(v,d) is even groot als de verzameling van alle mogelijke deelverzamelingen - de machtsverzameling of power setP
- vanD
·d.In een binair systeem vertegenwoordigt het aantal domein toestanden de hoeveelheid signaal, de signaalinhoud, of signaalcapaciteit, die wordt gemeten als het aantal domeinelementen d in bits (binary digits).
De waarden b(v,d) komen in een binair systeem overeen met de machten van 2. Zie reeks A000079 (eerder M1129, N0432) in de OEIS.
{ d ( b(2,d) :=
|
P
·d|
;:=
b (2,d -1 )*
2;:=
lg2 d bits;:=
A000079(d )|
(offset 0 ) )d }.
Bijv., bij (d
volgt (b(2,d)
=
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..
} );volgt (b(2,d)
=
{1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024,..
} ).Bereik.
Het getal b(v,d) blijft exponentieel in d.
(2 ≤
b(v,d)<
0 ^0 );
Complexiteitsklasse.
De verzameling
B
·(v,d) blijft binnen de klasse van de niet-aftelbaar oneindige verzamelingen (uncountable infinite sets), die de omvang hebben van het continuum (cardinality of the continuum ).Is dus alleen algoritmisch doorzoekbaar binnen exponentiële rekentijd (
EXP-TIME
).(B
·(v,d)
EXP-TIME
(d ) ).2.3.
Logische relaties.
Logische relaties geven het domein weer op een analytisch niveau.
Op semantisch niveau zijn dit de voorwaardelijke waarheidsbeweringen die mogelijk zijn met betrekking tot de toestand van het gehele domein of delen ervan.
In logische talen zijn dit bijv. waarheidswaardepatronen, formules, proposities, theorema's, e.d..
Deze komen overeen met de kolommen in de waarheidswaardetabel.
T
·(v,d) : De verzameling van alle mogelijke unieke logische relaties.Voorbeeld.
Bij twee waarheidswaarden (v
=
2, binair systeem) en twee items (d=
2), bestaat de verzameling logische relaties (T
·(v,d)) uit de volgende elementen (logische relaties), hier weergegeven met propositiesymbolen en in arbitraire volgorde:(T
·(v=
2,d=
2)=
{' T' ,' F' ,' A' ,' B' ,'¬A' ,'¬B'
,'( A B)' ,'( A ¬B)' ,'(¬
A B)' ,'(¬A ¬B)'
,'( A
B)' ,'( A ¬B)' ,'(¬
A B)' ,'(¬A ¬B)'
,'( A
B)' ,'( A
,'( A
B)' ,'( A ¬B)' ,'(¬
A B)' ,'(¬A ¬B)','( A
B)' ,'( A ¬B)' ,'(¬
A B)' ,'(¬A ¬B)','( A
B)' ,'( A #
B)' } ).Omvang.
t(v,d) : Het totale aantal mogelijke unieke logische relaties.
Het getal t(v,d) is het aantal volgordevariaties met teruglegging c.q. herhaling (herhalingsvariaties ) met omvang (lengte) b(v,d) uit v elementen.
{ v d
( t(v,d) :=
|
T
·(v,d)|
);:=
(b1 := 1, ..
b(v, d) ) v;:=
|
B
·(v,b( v,d))|
;:=
v ^|
B
·(v,d)|
;:=
v ^b(v,d );:=
v ^(v ^d):=
t(v,d -1 )*
v ) d, v }.In een binair systeem.
Onder (v
=
2 ) geldt:T
·(v,d) is even groot als de power set van de power set vanD
·d.De waarden t(v,d) komen in een binair systeem, overeen met de machten van 2 van de machten van 2. Zie reeks A001146 (eerder M1297, N0497) in de OEIS.
{ d ( t(2,d) :=
|
P
·b(2,d)|
;:=
|
P
·|P
·d|
|
);:=
t(2,d -1 )*
2;:=
A001146(d )|
(offset 0 ) )d }.
Bijv., { t(2, 1)
t(2, 2)
t(2, 3)
t(2, 4)
t(2, 5)
t(2, 6)
t(2, 7)
t(2, 8)
t(2, 9)
t(2, 10)
=
4,t(2, 2)
=
16,t(2, 3)
=
256,t(2, 4)
=
65536,t(2, 5)
=
4.294967 296 ·(10^ 9),t(2, 6)
=
1.844674 407370 955161 6 ·(10^ 19),t(2, 7)
=
3.402823 669209 384634 633746 074317 682114 56 ·(10^ 38),t(2, 8)
=
1.157920 892373 161954 235709 850086 879078 5326 ·(10^ 77),t(2, 9)
=
1.340780 792994 259709 957402 499820 584612 7479 ·(10^ 154),t(2, 10)
=
1.797693 134862 315907 729305 190789 024733 6179 ·(10^ 308),..
}.Bereik.
Het getal t(v,d) blijft hyperexponentieel in d.
(2 ≤
t(v,d)<
0 ^(0 ^
0 ) );
Complexiteitsklasse.
De verzameling
T
·(v,d) is algoritmisch doorzoekbaar binnen hyper-exponentiële rekentijd (2-EXP-TIME
).(T
·(v,d)
2-EXP-TIME
(d ) ).2.4.
De waarheidswaardetabel.
Gegeven een gekozen domein
D
·d en waardepalletV
· v worden de mogelijke directe logische relaties-tussen-relaties volledig gedefinieerd door middel van de zgn. waarheidswaardetabel.Deze wordt opgebouwd volgens een systematische waardetoekenning (validatie) van de objecten op basis van een simpel gestandaardiseerd rekenkundig schema (algoritme). De objecten doorlopen achtereenvolgens elk het gehele scala waarden via zgn. 'geneste' cycli (loops), waardoor ze hun unieke, geordende waarheidswaardepatronen verkrijgen. Vervolgens worden alle overige geordende waardencombinaties ingevuld. Op deze manier ontstaat de tabel als een sluitend, samenhangend geheel van alle mogelijke volgordes van (waarheids)waarden, oftewel (waarheids)waardepatronen t(v,d ), bij parameters {d,v}.
De waardepatronen zijn te vergelijken met uitspraken met minstens één gezegde c.q. hoofdzin of bijzin, oftewel 'zinnen'.
Ze hebben in een binair systeem de vorm van binaire getallen. Elk hiervan heeft een lengte van b(v,d ) waardeconstanten. De laatste zijn te vergelijken met lettertekens of symbolen in geschreven taal.
De lengte b(v,d) komt overeen met de hoeveelheid informatie in standaard eenheden: bits.
Bovendien geeft de tabel volkomen gegarandeerd alle mogelijke elementaire logische relaties weer in hun vaste, directe onderlinge logische relaties.
W
·(v,d)[T
] : De geordende verzameling van alle cellen in de waarheidswaardetabel.Voorbeeld.
De waarheidswaardetabel voor een logisch systeem met (v =2) waarden en (d=2) variabelen, geïnterpreteerd voor propositielogica (
PPL
), predikatenlogica (PDL
), resp. verkorte, Skolem vorm (Sk
).
Tabel tweewaardige waardencombinaties |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nr. | Waarde- patroon |
Logische relatie in PPL |
Logische relatie in PDL |
Logische relatie in Sk |
Logische kracht | ||||||
| 1 | 1 | 1 | 1 | 1 |
T |
¬F |
X ¬X |
0 | |||
| 2 | 0 | 0 | 0 | 0 |
F |
¬T |
X ¬X |
1 | |||
| 3 | 1 | 1 | 0 | 0 |
A1 |
¬¬A1 |
0.50 | ||||
| 4 | 1 | 0 | 1 | 0 |
A2 |
¬¬A2 |
0.50 | ||||
| 5 | 0 | 0 | 1 | 1 |
¬A1 |
¬A1 |
0.50 | ||||
| 6 | 0 | 1 | 0 | 1 |
¬A2 |
¬A2 |
0.50 | ||||
| 7 | 1 | 0 | 0 | 0 |
A1 A2 |
¬(¬A1 ¬A2) |
x A[x] |
¬ x ¬A[x] |
A[x] |
0.75 | |
| 8 | 0 | 1 | 0 | 0 |
A1 ¬A2 |
¬(¬A1 A2) |
0.75 | ||||
| 9 | 0 | 0 | 1 | 0 |
¬A1 A2 |
¬(A1 ¬A2) |
0.75 | ||||
| 10 | 0 | 0 | 0 | 1 |
¬A1 ¬A2 |
¬(A1 A2) |
A1\A2 |
¬x A[x] |
x ¬A[x] |
¬A[x] |
0.75 |
| 11 | 1 | 1 | 1 | 0 |
A1 A2 |
¬(¬A1 ¬A2) |
x A[x] |
¬x ¬A[x] |
A[cs] |
0.25 | |
| 12 | 1 | 1 | 0 | 1 |
A1 ¬A2 |
¬(¬A1 A2) |
A1 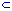A2 |
0.25 | |||
| 13 | 1 | 0 | 1 | 1 |
¬A1 A2 |
¬(A1 ¬A2) |
A1 A2 |
0.25 | |||
| 14 | 0 | 1 | 1 | 1 |
¬A1 ¬A2 |
¬(A1 A2) |
A1|A2 |
¬x A[x] |
x ¬A[x] |
¬A[cs] |
0.25 |
| 15 | 1 | 0 | 0 | 1 |
A1 A2 |
¬(A1#A2) |
(A1 A2)
(¬A1 ¬A2) |
0.50 | |||
| 16 | 0 | 1 | 1 | 0 |
A1#A2 |
¬(A1 A2) |
(A1 ¬A2)
(¬A1 A2) | 0.50 | |||
Omvang.
w(v,d)t : Het totale aantal cellen in de bijbehorende waarheidswaardetabel.
Het getal w(v,d)t wordt het product van het aantal rijen (domeintoestanden b(v,d)) en het aantal kolommen (toestandsrelaties t(v,d)).
{ v d
( w(v,d)t :=
|
W
·( 2,d)t|
;:=
|
(T
*(v,d ),B
*(v,d) )|
;:=
(|
T
*(v,d)|
*
|
B
*(v,d)|
);:=
(|
B
*(v,b(v,d))|
*
|
B
*(v,d)|
);:=
b(v,d)*
t(v,d);:=
v ^(v ^d )*
v ^d;:=
v ^((v ^d) +d ) ) d, v }.In een binair systeem.
Onder (v
=
2 ) geldt:{ d ( w(2,d)t
:=
|
W
·(2,d)t|
;:=
2 ^((2 ^d) +d ) )d }.
Bijv., { w(2, 1)t
w(2, 2)t
w(2, 3)t
w(2, 4)t
w(2, 5)t
w(2, 6)t
w(2, 7)t
w(2, 8)t
w(2, 9)t
w(2,10)t
Dezelfde reeks in bytes (8-bits):=
8,w(2, 2)t
=
64,w(2, 3)t
=
2018,w(2, 4)t
=
1.048576 ·(10^6),w(2, 5)t
=
1.374389 53472 ·(10^11),w(2, 6)t
=
1.180591 620717 411303 424 ·(10^21 ),w(2, 7)t
=
4.355614 296588 012332 331194 975126 633106 6368 ·(10^40 ),w(2, 8)t
=
2.964277 484475 294602 843417 216222 410441 0437 ·(10^79 ),w(2, 9)t
=
6.864797 660130 609714 981900 799081 393217 2694 ·(10^156 ),w(2,10)t
=
1.840837 770099 011489 514808 515367 961327 2248 ·(10^311 ),..
}.
{ 1,
8,
256,
1.31072 ·(10^5,
1.717986 9184 ·(10^10,
1.475739 525896 764129 28 ·(10^20,
5.444517 870735 015415 413993 718908 291383 2960 ·(10^39,
3.705346 855594 118253 554271 520278 013051 3046 ·(10^78,
8.580997 075163 262143 727375 998851 741521 5868 ·(10^155,
2.301047 212623 764361 893510 644209 951659 0310 ·(10^310,
NB. De waarden w(v,d)t·(2,d) komen niet voor als reeks in de
OEIS.8,
256,
1.31072 ·(10^5,
1.717986 9184 ·(10^10,
1.475739 525896 764129 28 ·(10^20,
5.444517 870735 015415 413993 718908 291383 2960 ·(10^39,
3.705346 855594 118253 554271 520278 013051 3046 ·(10^78,
8.580997 075163 262143 727375 998851 741521 5868 ·(10^155,
2.301047 212623 764361 893510 644209 951659 0310 ·(10^310,
..
}.2.5.
Redeneerelementen, argumenten (semantisch).
Wanneer we een redenering opzetten maken we gebruik van bepaalde mogelijke logische relaties over het onderwerp in kwestie. Een redenering bestaat dus uit een combinatie van logische relaties. Dat wil zeggen, een bepaalde selectie, of deelverzameling, uit
T
·(v,d). Zo'n combinatie kunnen we beschouwen als een 'pakket' van bouwstenen waarmee we een specifieke redenering kunnen maken. Elke bouwsteen kan fungeren als bewering, argument/premisse of conclusie .Op semantisch niveau zijn deze in elk geval gezuiverd van doublures.
Voor een solide oordeelsvorming moeten we rekening houden met alle mogelijke selecties.
U
·(v,d) : De verzameling van alle mogelijke unieke combinaties van redeneerelementen .Voorbeeld.
Bij twee waarheidswaarden (v
=
2, binair systeem) en één item (d=
1) bestaat de verzamelingU
·(v,d) uit de volgende deelverzamelingen (redeneervormen) hier weergegeven als combinaties van logische relaties gesteld in termen van propositiesymbolen, en in arbitraire volgorde:U
·(v=
2,d=
1)=
{ {}
,{' T'}
,{' T' ,' F'} {' T' ,' A'} {' T' ,'¬A'}
,{' T' ,' F' ,' A'} ,{' T' ,'F' ,'¬A'} ,{' T' ,' A' ,'¬A'}
,{' T' ,' F' ,' A' ,'¬A'}
,{' F'}
,{' F' ,' A'} ,{' F' ,'¬A'}
,{' F' ,' A' ,'¬A'}
,{' A'}
,{' A' ,'¬A'}
,{¬A'} }.
,{' T'}
,{' T' ,' F'} {' T' ,' A'} {' T' ,'¬A'}
,{' T' ,' F' ,' A'} ,{' T' ,'F' ,'¬A'} ,{' T' ,' A' ,'¬A'}
,{' T' ,' F' ,' A' ,'¬A'}
,{' F'}
,{' F' ,' A'} ,{' F' ,'¬A'}
,{' F' ,' A' ,'¬A'}
,{' A'}
,{' A' ,'¬A'}
,{¬A'} }.
Omvang.
u(v,d) : Het totale aantal mogelijke unieke combinaties van redeneerelementen.
Het getal u(v,d) is gelijk aan de som van alle mogelijke unieke ongeordende selecties (zonder interne herhaling) uit
T
·(v,d) - dus van de binomiaal coëfficiënten per deelverzameling vanU
·v,d van het aantal logische relaties t(v,d) boven de mogelijke lengte t1 van die deelverzameling.{ v d
( u(v,d) :=
|
U
·(v,d)|
; ( u1 ( (U
*[ u1]
U
·(v,d) )
( (u(v,d)[u1] :=
|
U
* [u1]|
) ( t1 ( (t1 =
u (v,d)[u1] ) ( (U
*[ u1]U
·t1 )
( U
·t1U
·(v ,d) ) ) )t1 ) ) )u1 ); ( u(v,d)
:=
(u1 := 1, ..
u(v, d) ) u(v,d)[u1];:=
(t1 := 1, ..
t(v, d) ) (|
U·t1|
);:=
(t1 := 1, ..
t(v, d) )binomial
(t(v,d), t1 );:=
|
T
·(v,t(v,d))|
;:=
2 ^|
T
·(v,d)|
;:=
2 ^(v ^(v ^d)) ) )d, v }.In een binair systeem.
Onder (v
=
2 ) geldt:U
·(v,d) is even groot als de power set van de power set van de power set vanD
·d.Enkele waarden u(2,d) komen overeen met getallen in de reeks A051285.
{ d ( u(2,d)
Bijv., u(2, 1)
u(2, 2)
u(2, 3)
u(2, 4)
u(2, 5)
u(2, 6)
u(2, 7)
u(2, 8)
u(2, 9)
u(2, 10)
=
16,u(2, 2)
=
65536,u(2, 3)
=
1.157920 892373 161954 235709 850086 879078 5327 ·(10^ 77),u(2, 4)
=
2.003529 930406 846464 979072 351560 255750 4478 ·(10^ 1.9728 ·(10 ^ 4) ),u(2, 5)
=
3.103280 543863 286140 299891 155863 640203 1970 ·(10^ 1.292913 986 ·(10 ^ 9) ),u(2, 6)
=
1.906974 011604 473384 552241 746745 187983 8889 ·(10^ 5.553023 288523 357132 ·(10 ^ 18) ),u(2, 7)
=
5.404596 770346 448769 045335 584018 890286 8344 ·(10^ 1.024351 994387 393637 500121 092501 032327 0013 ·(10 ^ 58) ),u(2, 8)
=
3.792584 931520 968368 388666 761840 860509 4478 ·(10^ 3.485689 212103 261792 986571 570093 041799 6503 ·(10 ^ 76) ),u(2, 9)
=
1.536561 964731 566339 928128 482575 903914 8145 ·(10^ 4.036152 363014 112689 691315 198542 699515 0356 ·(10 ^ 153) ),u(2, 10)
=
2.371036 276223 981569 086193 449295 336389 1223 ·(10^ 5.411595 565927 717197 055868 235175 883435 8915 ·(10 ^ 307) ),..
.Bereik.
Het getal u(v,d) blijft ultra-exponentieel in d.
(2 ≤
u(v,d)<
2 ^(0 ^(0 ^
0 ) ) ).Complexiteitsklasse.
De verzameling
U
·(v,d) blijft algoritmisch doorzoekbaar binnen ultra-exponentiële rekentijd (3-EXP-TIME
).(U
·(v,d)
3-EXP-TIME
(d ) ).2.6.
Redeneringen, afleidingen (semantisch).
Een zeer algemeen 'in de natuur' voorkomende manier van redeneren is die waarbij op zijn minst één denkstap wordt gezet. Typerend is daarbij dat er een inhoudelijk verschil is tussen de gedachte inhoud vóór de denkstap, en die erna. Daarnaast is de algemene aanname dat de tweede inhoud een bewerking of aanvulling bevat van de eerste.
(1)
Dat wil zeggen dat uit een bepaalde verzameling gegevens (feiten, verbanden) een andere verzameling gegevens wordt afgeleid.
Zo'n afleiding heeft als hoofdconnectief de implicatie.
Kort gezegd, elke redenering heeft de vorm 'premisse impliceert conclusie'.
Dit betekent dat zowel de premisse-groep als de conclusie-groep bestaat uit een bepaalde deelverzameling van
Deze krijgt globaal genomen de vorm:
{ v d
k1 k2 ( ( 
Bijv. (PPL):
(2)
{ v d
( 
(k1 := 1, (
k2 := 1,
Dit betekent dat de verzameling van alle mogelijke unieke redeneervormen onder de parameters
{v,d} wordt gevormd door een matrix:
{ v d
(
r(v,d)U: Het totale aantal van alle mogelijke unieke redeneringen c.q. gevolgtrekkingen op semantisch niveau.
De omvang van de verzameling wordt uiteraard gevormd door het Cartesisch product
(u(v,d) ·u(v,d)).
{ v d
( r(v,d)U
{ d ( r(2,d)U
De verzameling
(2)
Zoals gezegd bevat een verzameling
Redeneringen als afleiding.
Dat wil zeggen dat uit een bepaalde verzameling gegevens (feiten, verbanden) een andere verzameling gegevens wordt afgeleid.
Zo'n afleiding heeft als hoofdconnectief de implicatie.
Kort gezegd, elke redenering heeft de vorm 'premisse impliceert conclusie'.
Bijv.: (X Y ).
Y ).
NB. Aristotelis formuleerde een principe voor de reneervorm van het syllogisme dat in feite geldt voor elke redeneervorm:
"The syllogism is a discourse in which, certain things being laid down, another thing follows necessarily, simply because those things are laid down.
" (Aristotle, Prior Anal., 1, 1).
Een redenering in een systeem met een schaal van v waarden over een domein met d objecten zal dus de vorm hebben van
een afleiding met de vorm:
Bijv.: (X·(v,d) Y·(v,
d) ).
In het algemeen redeneren we vanuit een verzameling uitgangspunten (premissen) naar een verzameling conclusies.Y·(v,
d) ).Dit betekent dat zowel de premisse-groep als de conclusie-groep bestaat uit een bepaalde deelverzameling van
U
·(v,d).
(a) De premisse wordt gevormd door een bepaalde deelverzameling uit
(b) De conclusie wordt gevormd door een (andere of dezelfde) deelverzameling zeg
U
·(v,d) , zegU
·(v,d)[k1] met lengte (omvang) l[ k1] elementen.(b) De conclusie wordt gevormd door een (andere of dezelfde) deelverzameling zeg
U
·(v ,d)[k2] met lengte (omvang) l[k2] elementen.R
·(v,d)[k1,k2]: Een redenering van (een element van)U
·(v,d) naar (een element van)U
·(v, d).Deze krijgt globaal genomen de vorm:
{ v d
k1 k2 ( R
·( v,d)[k1,k2] ( U
·( v,d)[k1]U
·(v, d)[k2] ) )k2, k1, d, v }.
{ v1 d1 ( v1
k1 k2
( (
(
(
( ¬C ) };
( B ), (C ¬D
) } );
¬C ) )
(¬A B ), (C ¬D ) ) )
k2, k1 )d1, v1 }.
v1 d1 ( v1 =
2; d1=
4;D
·d1=
{A, B, C , D };k1 k2
( (U
·(v1,d1)[k1]U
·(v1,d1) );(U
·(v1,d1)[k2]
U
·(v1,d1) );(U
·(v1,d1)[k1]
U
·(v1,d1)[k2] );(U
·(v1,d1)[k1]=
{A, (B ¬C ) };(U
·(v1,d1)[k2]=
{¬A B ), (C ¬D
) } );R
·(v,d)[k1,k2]:=
((A, (B ¬C ) )
(¬A B ), (C ¬D ) ) )
k2, k1 )d1, v1 }.(2)
De verzameling van afleidingen.
R
·(v,d)[U
]: De verzameling van alle mogelijke unieke redeneringen c.q. gevolgtrekkingen op semantisch niveau. { v d
( R
·(v,d)[U
]:=
(k1 := 1, ..
u(v,d) ) (
k2 := 1, ..
u(v,d) )R
·(v,d) [U
][k1,k2] k2, k1 )d , v }.Dit betekent dat de verzameling van alle mogelijke unieke redeneervormen onder de parameters
{v,d} wordt gevormd door een matrix: { v d
( R
·(v,d)[U
]:=
(U
·(v,d)X
U
·(v,d) ) ) d, v }.Omvang.
r(v,d)U: Het totale aantal van alle mogelijke unieke redeneringen c.q. gevolgtrekkingen op semantisch niveau.
De omvang van de verzameling wordt uiteraard gevormd door het Cartesisch product
(u(v,d) ·u(v,d)). { v d
( r(v,d)U :=
|
R
·(v ,d)[U
]|
;:=
u(v,d)^2 ;:=
v^(2*
t(v,d) ) )d , v }.In een binair systeem.
{ d ( r(2,d)U
:=
|
R
·(2,d)[U
]|
;:=
u(2,d)^2;:=
2^(2*
t(2,d) ):=
)d, v }.
Bijv., { r(2, 1)
r(2, 2)
r(2, 3)
r(2, 4)
r(2, 5)
r(2, 6)
r(2, 7)
r(2, 8)
r(2, 9)
r(2, 10)
=
256,r(2, 2)
=
429496 7296,r(2, 3)
=
1.340780 792994 259709 957402 499820 584612 7479 ·(10^ 154),r(2, 4)
=
4.014132 182036 063039 166060 606038 876734 3771 ·(10^ 3.9456 ·(10 ^ 4) ),r(2, 5)
=
9.630350 133920 413014 213703 778052 746804 2213 ·(10^ 2.585827 972 ·(10 ^ 9) ),r(2, 6)
=
3.636549 880934 858190 730055 838296 676980 3584 ·(10^ 1.110604 657704 671426 4 ·(10 ^ 19) ),r(2, 7)
=
2.920966 625003 926469 642581 049794 912721 3645 ·(10^ 2.048703 988774 787275 000242 185002 064654 0026 ·(10 ^ 58) ),r(2, 8)
=
1.438368 435388 603127 724431 746286 617796 3432 ·(10^ 6.971378 424206 523585 973143 140186 083599 3006 ·(10 ^ 76) ),r(2, 9)
=
2.361022 671459 731320 687702 749778 179430 9461 ·(10^ 8.072304 726028 225379 382630 397085 399030 0713 ·(10 ^ 153) ),r(2, 10)
=
5.621813 023170 085026 967697 421355 931681 4924 ·(10^ 1.082319 113185 543439 411173 647035 176687 1783 ·(10 ^ 308) ),..
}.Complexiteitsklasse.
De verzameling
R
·(v,d)[U
]: blijft van hetzelfde complexiteitsniveau alsU
·(v,d).(2)
Afleidingen zijn op semantisch niveau tweeplaatsig.
Zoals gezegd bevat een verzameling
U
·(v,d) deelverzamelingenU
·(v,d)[k1] die elk bestaan uit unieke combinaties van logische relaties uit de verzamelingT
·(v,d). Al die elementen hebben hun eigen logische geldigheidswaarde die uniek is binnenT
·(v,d). Wanneer we deze waarden combineren, bijvoorbeeld in een premisse of conclusie binnen een afleiding, volgt volgens de logische wetten op semantisch niveau onmiddelijk parafrase reductie van de combinatie naar één logische geldigheidswaarde die weer overeenkomt met één logische relatie inT
·(v,d). Dit betekent dat premisse en conclusie elk per saldo (nogmaals: op semantisch niveau) maar één element bevatten. Daarom kunnen we logische afleidingen op semantisch niveau rekenen als proposities met twee enkelvoudige elementen.2.7.
Minimale redeneringen, afleidingen (semantisch).
(1)
Elk van de deelverzamelingen in de twee componenten van de afleiding kan dus altijd volgens logische wetten worden gereduceerd tot de kleinst mogelijke logisch-semantische inhoud: in dit geval logische relaties in een domein met d objecten.
Daarbij beschouwen we de componenten zoals gezegd in conjunctie.
We gaan voor het gemak uit van een binair systeem. Dit heeft altijd 2 waarden: valentie
De verzameling mogelijke redeneringen kan dus gereduceerd worden tot haar
parafrase reduct versie op semantisch niveau.
(v d k1
k2 (
(
(
(
p1
q1 ( (
(p1 := 1, (q1 := 1,
De parafrase reduct versies van premisse en conclusie zullen elk dus bestaan uit precies één element
uit elk van de oorspronkelijke deelverzamelingen k1, k2, uit
Dit betekent dat de verzameling van alle mogelijke unieke minimale redeneervormen
onder de parameters {v,d} wordt gevormd door een matrix:
(v d
r(v,d)T: Het totale aantal van alle mogelijke unieke minimale redeneringen c.q. gevolgtrekkingen.
De omvang van deze verzameling wordt uiteraard gevormd door het Cartesisch product
(t(v,d) ·t(v,d)).
{ v d
( r(v,d)T
{ d ( r(2,d)T
De verzameling
(2)
Uiteindelijk willen we weten of een redenering steekhoudend is, oftewel geldig.
Welke van de afleidingsrelaties uit de matrix
Elk element van de matrix
(3)
Het totale aantal van alle mogelijke unieke contradictoire redeneringen c.q. gevolgtrekkingen is simpelweg hetzelfde als dat van elke verzameling disjuncties: precies één.
Het totale aantal van alle mogelijke unieke consistente redeneringen c.q. gevolgtrekkingen is dus simpelweg r(v ,d)T -1.
xT: Het totale aantal van alle mogelijke unieke valide redeneringen c.q. gevolgtrekkingen.
De formule voor het aantal valide afleidingsrelaties xT bij valentie v =2 en aantal objecten d is:
De waarden x(2,d)T komen goeddeels overeen met de machten van 2 van de machten van 3. Zie A011764 in de OEIS .
De verzameling
(4)
Hieronder volgt een tabel met de belangrijkste afmetingen van de hierboven genoemde verzamelingen.
Deze tabel laat zien hoe de combinatorische mogelijkheden in een simpel logisch systeem al gauw leiden tot een zoekruimte van astronomische proporties. Met 10000 items kun je bijvoorbeeld een aantal 'minimale redeneringen' maken (op semantisch niveau ) waarvan het getal bestaat uit een aantal cijfers waarbij alleen al de lengte van het getal kan worden weergegeven met een exponent (decimaal logaritme) die op zijn beurt een lengte heeft van 3011 cijfers. Anders gezegd, niet het getal zelf is 3011 cijfers lang, maar de exponent waarmee je haar lengte weergeeft.
(5)
Om de bovenstaande getallen enigszins in perspectief te plaatsen volgen hieronder enkele voorbeelden van grote aantallen in de natuur (alle volgens tamelijk ruwe schattingen).
• De lichtsnelheid (in vacuüm) in kilometers per seconde: 2,99792458 *10^5.
• Een astronomische eenheid (AE, internationaal au of ua) in kilometers: 1,495978707 *10^8.
• Een lichtjaar in kilometers: ca. 9,46 *10^12.
• De doorsnede van het zichtbare universum in lichtjaren: 9,3 *10^10.
• De doorsnede van het zichtbare universum in kilometers: 8,8 *10^23.
• Het aantal clusters van sterrenstelsels: ca. 4 ·10 ^8.
• Het aantal sterrenstelsels in het heelal: minstens 2 *10 ^11.
• Het aantal sterren per sterrenstelsel: ca. 10^8 tot 10^14.
• Het aantal sterren in 'ons' sterrenstelsel, de Melkweg: ca. 10^11.
• Het aantal sterren in het waarneembare heelal: ca. 10 ^22.
• Het aantal moleculen in het waarneembare heelal: ca. 10 ^80.
• Constante van Avogadro, het aantal deeltjes (bijv. atomen, moleculen, ionen, enz.) in één mol chemische stof: 6,02214076 *10 ^23.
• Omtrek van de evenaar van de aarde in kilometers: 40075,0166856.
• Maximale aantal cycli van licht per seconde rond de evenaar van de aarde: 26930,814710996834.
• Het totale aantal vissen in de oceanen: ca. 3,5 ·10 ^9.
• Het aantal mieren op aarde: ca. 3,5 ·10 ^12.
• Het totale aantal zandkorrels op alle stranden op aarde: ca. 10 ^21.
• Het aantal verschillende eiwitten die zijn op te bouwen uit 100 aminozuren: ca. 10 ^130.
• Het aantal cellen in het menselijk lichaam: ca. 10 ^14.
• Het totaal aantal zenuwcellen in het menselijk lichaam: ca. 10 ^11.
• Het aantal zenuwcellen in de menselijke hersenen: gemiddeld ca. 8,6 ^10.
• Het aantal neuronale verbindingen in de menselijke hersenen: ca. 10 ^14.
Om er twee voorbeelden uit te lichten:
Met 5 items kun je al bijna zoveel -unieke, minimale- redeneringen maken als het totale aantal zandkorrels op alle stranden op aarde.
Met 7 items, de gemiddelde geheugencapaciteit van ons bewuste aandachtsvenster, kun je al bijna zoveel -unieke, minimale- redeneringen maken als er moleculen zijn in het waarneembare heelal.
Deze -letterlijk- astronomische getallen geven het niveau van complexiteit weer en daarmee die van beslisproblemen.
Daarbij helpt het niet om te denken aan een meer geavanceerd logisch systeem. Als algemene regel geldt: hoe geavanceerder het logische systeem, hoe meer expressief vermogen het heeft, maar hoe minder beslisvermogen. Met elke stap naar een meer geavanceerd logisch systeem, zoals modale logica, meerwaardige logica, predikatenlogica, enz., en ook zgn. 'fuzzy logica', nemen de aantallen, zoek-, complexiteits- en beslisbaarheidsproblemen enkel maar opnieuw explosief toe!
Zonder voldoende kennis en kunde van logische bewijsvoering en toetsing is het al nagenoeg onmogelijk om mogelijke redeneringen te beoordelen over meer dat twee items.
De verzameling redeneringen in hun minimale parafrasevorm .
Elk van de deelverzamelingen in de twee componenten van de afleiding kan dus altijd volgens logische wetten worden gereduceerd tot de kleinst mogelijke logisch-semantische inhoud: in dit geval logische relaties in een domein met d objecten.
Daarbij beschouwen we de componenten zoals gezegd in conjunctie.
We gaan voor het gemak uit van een binair systeem. Dit heeft altijd 2 waarden: valentie
(v
Dit systeem kent een aantal logische relaties zoals we eerder zagen:=
2 ).
(t(v,d)
=
v ^(v ^d ) ).De verzameling mogelijke redeneringen kan dus gereduceerd worden tot haar
parafrase reduct versie op semantisch niveau.R
·(v,d)[T
] De verzameling van alle mogelijke unieke minimale redeneringen c.q. gevolgtrekkingen op semantisch niveau.(v d |
(k1
k2 ( R
·(v,d)[U
][k1,k2 ](U
·(v,d)[k1] in conjunctieU
·(v,d)[k2] in conjunctie );(Cj
(U
·(v,d)[k1 ]Cj
(U
·(v,d) [k2] );(U
·(v,d)[k1]syn
par-rdc
U
·(v,d )[k2]syn
par-rdc
);par-rdc
(p1
q1 ( (T
·(v,d)[p1]
T
·(v,d)[q1] );R
·(v,d)[T
] [p1,q1] ;R
·(v,d)[T
]:=
(p1 := 1, ..
u(v,d) ) (q1 := 1, ..
u(v,d) )R
·(v,d)[T
][p1,q1] ) ) );De parafrase reduct versies van premisse en conclusie zullen elk dus bestaan uit precies één element
uit elk van de oorspronkelijke deelverzamelingen k1, k2, uit U
·(v,d ).Dit betekent dat de verzameling van alle mogelijke unieke minimale redeneervormen
onder de parameters {v,d} wordt gevormd door een matrix:(v d |
R
·(v,d) [T
]:=
(T
·(v,d)X
T
·(v,d) );Omvang.
r(v,d)T: Het totale aantal van alle mogelijke unieke minimale redeneringen c.q. gevolgtrekkingen.
De omvang van deze verzameling wordt uiteraard gevormd door het Cartesisch product
(t(v,d) ·t(v,d)). { v d
( r(v,d)T :=
|
R
·(v ,d)[T
]|
;:=
t(v,d)^2 ;:=
v^(2*
b(v,d) ) )d , v }.In een binair systeem.
{ d ( r(2,d)T
:=
|
R
·(2,d)[T
]|
;:=
t(2,d)^2;:=
t(2,d+1);:=
2^(2*
b(2,d) );:=
A001146(d )^2;:=
A001146(d +1 )|
(offset 0 ) )d }.
Bijv., { r(2, 1)T
r(2, 2)T
r(2, 3)T
r(2, 4)T
r(2, 5)T
r(2, 6)T
r(2, 7)T
r(2, 8)T
r(2, 9)T
r(2,10)T
=
16,r(2, 2)T
=
256,r(2, 3)T
=
65536,r(2, 4)T
=
4.294967 296 ·(10^ 9),r(2, 5)T
=
1.844674 407370 955161 6 ·(10^ 19),r(2, 6)T
=
3.402823 669209 384634 633746 074317 682114 56 ·(10^ 38),r(2, 7)T
=
1.157920 892373 161954 235709 850086 879078 5326 ·(10^ 77),r(2, 8)T
=
1.340780 792994 259709 957402 499820 584612 7479 ·(10^ 154),r(2, 9)T
=
1.797693 134862 315907 729305 190789 024733 6179 ·(10^ 308),r(2,10)T
=
3.231700 607131 100730 071487 668866 995196 0444 ·(10^ 616),..
}.Complexiteitsklasse.
De verzameling
R
·(v,d)[T
]: blijft van hetzelfde complexiteitsniveau alsT
·(v,d).(2)
Evaluatie van redeneringen.
Uiteindelijk willen we weten of een redenering steekhoudend is, oftewel geldig.
Welke van de afleidingsrelaties uit de matrix
R
·(v,d)[T
] zijn nu geldig?Elk element van de matrix
R
·(v,d)[T
] is als implicatie simpel op te lossen volgens de regels van de algemene waarheidswaardetabel.
Zie boven, 2.4. Waarheidswaardetabel.
Zie ook: Principes van Logische bewijsvoering; (4.1a) Methode van Waarheidswaardentabellen.
En: Bewijsmethode voor Propositielogica: de Waarheidswaardentabel-methode .
Zie ook: Principes van Logische bewijsvoering; (4.1a) Methode van Waarheidswaardentabellen.
En: Bewijsmethode voor Propositielogica: de Waarheidswaardentabel-methode .
(2.1)
Elk van de logische relaties in de componenten van
Elk van deze waardepatronen is element van de verzameling (waardepatronen van) logische relaties
Dit betekent, zoals we zagen, dat elk van deze binaire patronen een lengte heeft van:
De uitkomsten bestaan weer uit binaire waarheidswaardepatronen.
(2.3)
Regels voor interpretatie van een binair waarheidswaardepatroon:
Codering als binaire getallen.
Elk van de logische relaties in de componenten van
R
·(v,d)[T
] kan in het meest simpele logische systeem, propopositielogica (PPL), worden gecodeerd als binaire waarheidswaardepatroon.Elk van deze waardepatronen is element van de verzameling (waardepatronen van) logische relaties
T
·( v,d)[k1].Dit betekent, zoals we zagen, dat elk van deze binaire patronen een lengte heeft van:
b(v,d)·(v,d)
(2.2) =
v·^d .Parafrase-reductie tot één binair getal.
De uitkomsten bestaan weer uit binaire waarheidswaardepatronen.
(2.3)
Interpretatie van de binaire uitkomst.
Regels voor interpretatie van een binair waarheidswaardepatroon:
(a) Niet alle bits staan op 0 of 1 : onbeslistheid, indefinitiet contingentie.
(b) Alle bits staan op 0 of 1 : beslistheid.
(b) Alle bits staan op 0 of 1 : beslistheid.
(b1) Alle bits staan op 0 : contradictie (onvervulbaarheid).
Alleen het geval indien 'waar impliceert onwaar' (d.w.z.
(b2) Niet alle bits staan op 0, en evenmin op 1 : (definitiet) contingentie.
Alleen het geval indien 'waar impliceert onwaar' (d.w.z.
$
1 $
0 ).(b2) Niet alle bits staan op 0, en evenmin op 1 : (definitiet) contingentie.
(b2.1) Niet alle bits staan op 1 : ongeldigheid (vooronderstelling, c.q. drogreden).
(b2.2) Niet alle bits staan op 0 : consistentie (vervulbaarheid).
(b3) Alle bits staan op 1 : validiteit.(b2.2) Niet alle bits staan op 0 : consistentie (vervulbaarheid).
(3)
Geldige redeneringen.
Het totale aantal van alle mogelijke unieke contradictoire redeneringen c.q. gevolgtrekkingen is simpelweg hetzelfde als dat van elke verzameling disjuncties: precies één.
Het totale aantal van alle mogelijke unieke consistente redeneringen c.q. gevolgtrekkingen is dus simpelweg r(v ,d)T -1.
Omvang.
xT: Het totale aantal van alle mogelijke unieke valide redeneringen c.q. gevolgtrekkingen.
De formule voor het aantal valide afleidingsrelaties xT bij valentie v =2 en aantal objecten d is:
x(v,d)T
:=
(v +1)·^b(v,d );:=
(v +1)·^(v ^d);In een binair systeem.
De waarden x(2,d)T komen goeddeels overeen met de machten van 2 van de machten van 3. Zie A011764 in de OEIS .
Bijv., { x(2, 1)T
x(2, 2)T
x(2, 3)T
x(2, 4)T
x(2, 5)T
x(2, 6)T
x(2, 7)T
x(2, 8)T
x(2, 9)T
x(2,10)T
Dezelfde reeks als percentages geldige implicaties:=
9,x(2, 2)T
=
81,x(2, 3)T
=
6561,x(2, 4)T
=
4.304672 1 ·(10 ^7 ),x(2, 5)T
=
1.853020 188851 841 ·(10 ^15 ),x(2, 6)T
=
3.433683 820292 512484 657849 089281 ·(10 ^30 ),x(2, 7)T
=
1.179018 457773 858317 152087 286141 251866 5678 ·(10 ^61 ),x(2, 8)T
=
1.390084 523771 447327 649397 867896 613031 1422 ·(10 ^122 ),x(2, 9)T
=
1.932334 983228 891510 545406 872201 958105 5401 ·(10 ^244 ),x(2,10)T
=
3.733918 487410 200435 329597 541848 665882 2541 ·(10 ^488 ),..
}.
{ 56.25%,
31.640625%,
10.011291 503906 25%,
1.002259 575761 854648 590087 890625%,
1.004524 257206 332858 195774 182519 244277 5005 ·(10 ^-002)%,
1.009068 983315 934771 190166 090841 089949 3574 ·(10 ^-006)%,
1.018220 213090 254245 618211 973419 191101 3791 ·(10 ^-014)%,
1.036772 402345 562763 403206 053360 190738 2718 ·(10 ^-030)%,
1.074897 014265 389476 630012 892337 230410 6700 ·(10 ^-062)%,
1.155403 591276 648908 023678 855815 537058 0566 ·(10 ^-126)%,
31.640625%,
10.011291 503906 25%,
1.002259 575761 854648 590087 890625%,
1.004524 257206 332858 195774 182519 244277 5005 ·(10 ^-002)%,
1.009068 983315 934771 190166 090841 089949 3574 ·(10 ^-006)%,
1.018220 213090 254245 618211 973419 191101 3791 ·(10 ^-014)%,
1.036772 402345 562763 403206 053360 190738 2718 ·(10 ^-030)%,
1.074897 014265 389476 630012 892337 230410 6700 ·(10 ^-062)%,
1.155403 591276 648908 023678 855815 537058 0566 ·(10 ^-126)%,
..
}.Complexiteitsklasse.
De verzameling
X
·(v,d)[T
]: blijft van hetzelfde complexiteitsniveau alsT
·(v,d).(4)
Tabel.
Hieronder volgt een tabel met de belangrijkste afmetingen van de hierboven genoemde verzamelingen.
|
Combinatorische explosie in logisch systeem (PPL) |
|||||
|---|---|---|---|---|---|
|
Waarheidswaarden (valentie) v =2 (Binair systeem) |
|||||
Unieke items |
Domein toestanden |
Logische relaties |
Tupels (paren) van formules |
Valide implicaties |
Valide implicaties |
d |
b(v,d) |
t(v,d) |
r(v,d)T |
x(v,d)T |
%(x/t)(v,d)T |
|
1 |
2 |
4 |
16 |
9 | 56.25% |
|
2 |
4 |
16 |
256 |
81 |
31.640 625% |
|
3 |
8 |
256 |
65536 |
6561 |
10.011291 503906 25% |
|
4 |
16 |
65536 |
429496 7296 |
430467 21 |
1.002259 575761 854649% |
|
5 |
32 |
429496 7296 |
1.844674 407371 955162 ·(10 ^019 [ 2] ) |
1.853020 188851 841 ·(10 ^015 [ 2] ) |
1.004524 257206 332858 ·(10 ^-002 )% |
|
6 |
64 |
1.844674 407370 955162 ·(10 ^019 [ 2] ) |
3.402823669 209384635 ·(10 ^038 [ 2] ) |
3.433683 820292 512485 ·(10 ^030 [ 2] ) |
1.009068 983315 934771 ·(10 ^-006 )% |
|
7 |
128 |
3.402823 669209 384635 ·(10 ^038 [ 2] ) |
1.157920 892373 161954 ·(10 ^077 [ 2] ) |
1.179018 457773 858317 ·(10 ^061 [ 2] ) |
1.018220 213090 254246 ·(10 ^-014 [ 2] )% |
|
8 |
256 |
1.157920 892373 161954 ·(10 ^077 [ 2] ) |
1.340780792 994259710 ·(10 ^154 [ 3] ) |
1.390084 523771 447328 ·(10 ^122 [ 3] ) |
1.036772 402345 562763 ·(10 ^-030 [ 2] )% |
|
9 |
512 |
1.340780 792994 ·(10 ^154 [ 3] ) |
1.797693 134862 315907 ·(10 ^308 [ 3] ) |
1.932334 983228 891511 ·(10 ^244 [ 3] ) |
1.074897 014265 389476 ·(10 ^-062 [ 2] )% |
|
10 |
1024 |
1.797693 134862 315907 ·(10 ^308 [ 3] ) |
3.231700 607131 100730 ·(10 ^616 [ 3] ) |
3.733918 487410 200435 ·(10 ^488 [ 3] ) |
1.155403 591276 648908 ·(10 ^-126 [ 3] )% |
|
10 ^2 |
1.267650 600228 229401 ·(10 ^30 [ 2] ) |
2.285367 694229 513703 ·(10 ^3.816008 546901 470562 ·(10 ^29 [ 2] ) ) |
5.222905 497827 924040 ·(10 ^7.632017 093802 941125 ·(10 ^29 [ 2]) ) |
2.561263 804102 827066 ·(10 ^6.048230 449270 260188 ·(10 ^29 [ 2]) ) |
4.903906 082865 165216 ·(10 ^-1.583786 644532 680936 ·(10 ^29 [ 2]) ) % |
|
10 ^3 |
1.071508 607186 267321 ·(10 ^301 [ 3] ) |
7.096672 219435 693805 ·(10 ^3.225562 313752 005814 ·(10 ^300 [ 3] ) ) |
5.036275 659011 033621 ·(10 ^6.451124 627504 011628 ·(10 ^300 [ 3] ) ) |
1.296912 946078 858393 ·(10 ^5.112395 311036 297716 ·(10 ^300 [ 3] ) ) |
2.575142 891073 463136 ·(10 ^-1.338729 316467 713912 ·(10 ^300 [ 3] ) )% |
|
10 ^4 |
1.995063 116880 758385 ·(10 ^3010 [ 4] ) |
6.467855 830387 433571 ·(10 ^(6.005738 414239 835051 ·(10 ^3009 [ 4] ) ) |
4.183315 904267 671786 ·(10 ^(1.201147 682847 967010 ·(10 ^3010 [ 4] ) ) |
1.968225 299623 265918 ·(10 ^(9.518870 175710 679943 ·(10 ^3009 [ 4] ) ) |
4.704940 637199 671382 ·(10 ^(-2.492606 652768 990158 ·(10 ^3009 [ 4] ) ) % |
|
10 ^5 |
9.990020 930143 845079 ·(10 ^30102 [ 5] ) |
1.022672 567782 053958 ·(10 ^(+3.007295 957284 283071 ·(10 ^30102 [ 5] ) ) % |
1.045859 180893 939748 ·(10 ^(+6.014591 914568 566142 ·(10 ^30102 [ 5] ) ) % |
1.376624 183690 244770 ·(10 ^(+4.766451 320865 920576 ·(10 ^30102 [ 5] ) ) % |
1.316261 509043 298055 ·(10 ^(-1.248140 593702 645566 ·(10 ^30102 [ 5] ) ) % |
Deze tabel laat zien hoe de combinatorische mogelijkheden in een simpel logisch systeem al gauw leiden tot een zoekruimte van astronomische proporties. Met 10000 items kun je bijvoorbeeld een aantal 'minimale redeneringen' maken (op semantisch niveau ) waarvan het getal bestaat uit een aantal cijfers waarbij alleen al de lengte van het getal kan worden weergegeven met een exponent (decimaal logaritme) die op zijn beurt een lengte heeft van 3011 cijfers. Anders gezegd, niet het getal zelf is 3011 cijfers lang, maar de exponent waarmee je haar lengte weergeeft.
(5)
Ter vergelijking.
Om de bovenstaande getallen enigszins in perspectief te plaatsen volgen hieronder enkele voorbeelden van grote aantallen in de natuur (alle volgens tamelijk ruwe schattingen).
In het heelal.
• De lichtsnelheid (in vacuüm) in kilometers per seconde: 2,99792458 *10^5.
• Een astronomische eenheid (AE, internationaal au of ua) in kilometers: 1,495978707 *10^8.
• Een lichtjaar in kilometers: ca. 9,46 *10^12.
• De doorsnede van het zichtbare universum in lichtjaren: 9,3 *10^10.
• De doorsnede van het zichtbare universum in kilometers: 8,8 *10^23.
• Het aantal clusters van sterrenstelsels: ca. 4 ·10 ^8.
• Het aantal sterrenstelsels in het heelal: minstens 2 *10 ^11.
• Het aantal sterren per sterrenstelsel: ca. 10^8 tot 10^14.
• Het aantal sterren in 'ons' sterrenstelsel, de Melkweg: ca. 10^11.
• Het aantal sterren in het waarneembare heelal: ca. 10 ^22.
• Het aantal moleculen in het waarneembare heelal: ca. 10 ^80.
• Constante van Avogadro, het aantal deeltjes (bijv. atomen, moleculen, ionen, enz.) in één mol chemische stof: 6,02214076 *10 ^23.
Op aarde.
• Omtrek van de evenaar van de aarde in kilometers: 40075,0166856.
• Maximale aantal cycli van licht per seconde rond de evenaar van de aarde: 26930,814710996834.
• Het totale aantal vissen in de oceanen: ca. 3,5 ·10 ^9.
• Het aantal mieren op aarde: ca. 3,5 ·10 ^12.
• Het totale aantal zandkorrels op alle stranden op aarde: ca. 10 ^21.
• Het aantal verschillende eiwitten die zijn op te bouwen uit 100 aminozuren: ca. 10 ^130.
In het menselijk lichaam.
• Het aantal cellen in het menselijk lichaam: ca. 10 ^14.
• Het totaal aantal zenuwcellen in het menselijk lichaam: ca. 10 ^11.
• Het aantal zenuwcellen in de menselijke hersenen: gemiddeld ca. 8,6 ^10.
• Het aantal neuronale verbindingen in de menselijke hersenen: ca. 10 ^14.
Met 5 items kun je al bijna zoveel -unieke, minimale- redeneringen maken als het totale aantal zandkorrels op alle stranden op aarde.
Met 7 items, de gemiddelde geheugencapaciteit van ons bewuste aandachtsvenster, kun je al bijna zoveel -unieke, minimale- redeneringen maken als er moleculen zijn in het waarneembare heelal.
Deze -letterlijk- astronomische getallen geven het niveau van complexiteit weer en daarmee die van beslisproblemen.
Daarbij helpt het niet om te denken aan een meer geavanceerd logisch systeem. Als algemene regel geldt: hoe geavanceerder het logische systeem, hoe meer expressief vermogen het heeft, maar hoe minder beslisvermogen. Met elke stap naar een meer geavanceerd logisch systeem, zoals modale logica, meerwaardige logica, predikatenlogica, enz., en ook zgn. 'fuzzy logica', nemen de aantallen, zoek-, complexiteits- en beslisbaarheidsproblemen enkel maar opnieuw explosief toe!
Zonder voldoende kennis en kunde van logische bewijsvoering en toetsing is het al nagenoeg onmogelijk om mogelijke redeneringen te beoordelen over meer dat twee items.
C.P. van der Velde © 2014, 2018.